【表盘识别】基于matlab Hough变换钟表表盘识别【含Matlab源码 1069期】

一、Hough简介

霍夫变换(Hough Transform)是图像处理中的一种特征提取技术，它通过一种投票算法检测具有特定形状的物体。该过程在一个参数空间中通过计算累计结果的局部最大值得到一个符合该特定形状的集合作为霍夫变换结果。霍夫变换于1962年由Paul Hough 首次提出[53]，后于1972年由Richard Duda和Peter Hart推广使用[54]，经典霍夫变换用来检测图像中的直线，后来霍夫变换扩展到任意形状物体的识别，多为圆和椭圆。

霍夫变换运用两个坐标空间之间的变换将在一个空间中具有相同形状的曲线或直线映射到另一个坐标空间的一个点上形成峰值，从而把检测任意形状的问题转化为统计峰值问题，上一节中已经介绍了车道的直线特征，本节中介绍hough变换检测直线的原理和检测结果。

我们知道，一条直线在直角坐标系下可以用y=kx+b表示, 霍夫变换的主要思想是将该方程的参数和变量交换，即用x,y作为已知量k,b作为变量坐标，所以直角坐标系下的直线y=kx+b在参数空间表示为点(k,b)，而一个点(x1,y1)在直角坐标系下表示为一条直线y1=x1·k+b，其中(k,b)是该直线上的任意点。为了计算方便，我们将参数空间的坐标表示为极坐标下的γ和θ。因为同一条直线上的点对应的(γ,θ)是相同的，因此可以先将图片进行边缘检测，然后对图像上每一个非零像素点，在参数坐标下变换为一条直线，那么在直角坐标下属于同一条直线的点便在参数空间形成多条直线并内交于一点。因此可用该原理进行直线检测。

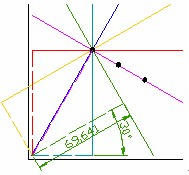
如图 所示，对于原图内任一点(x,y)都可以在参数空间形成一条直线，以图中一条直线为例有参数(γ,θ)=(69.641,30°)，所有属于同一条直线上的点会在参数空间交于一点，该点即为对应直线的参数。由该图中所有直线所得到的(γ,θ)在参数空间中得到一系列对应曲线见图 霍夫统计变换结果。

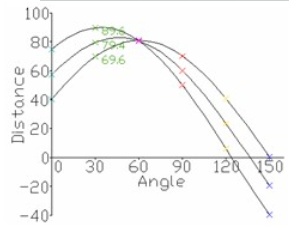
二、部分源代码

clear all;
close all;
clc;
P= imread('时钟-2.jpg');  %2/5/8/11 没问题 7/10反  13图分针错 16图时针错

I = imresize(P,0.7);  % 图像缩小70%
% figure('NumberTitle', 'off', 'Name', '原图');
% imshow(I);
% 去除背景
[m,n]=size(I);
for i=1:m 
    for j=1:n 
        if I(i,j)>100 
            I(i,j)=256; 
        end
    end
end
imshow(I);

I1 = im2bw(I);  %rgb转化为二值化图像
% figure('NumberTitle', 'off', 'Name', '二值化后图像');
% imshow(I1);

% I2 = edge(I1,'canny');  %canny 算子提取边界
% figure(3)
% imshow(I2)

I20 = imcomplement(I1); %图像反色
% figure('NumberTitle', 'off', 'Name', '反色后图像');
 imshow(I20);

I2 = bwmorph(I20,'skel',8); %提取图像骨架 6ci   N=6、7、8、9都行  10图取3  11图取5
% figure('NumberTitle', 'off', 'Name', '提取图像骨架');
imshow(I2);

%检测直线
[H,T,R] = hough(I2);  
figure('NumberTitle', 'off', 'Name', '峰值提取效果');
imshow(H,[],'XData',T,'YData',R, 'InitialMagnification','fit');
xlabel('\theta'), ylabel('\rho');
axis on, axis normal, hold on;
P  = houghpeaks(H,5,'threshold',ceil(0.3*max(H(:))));
x = T(P(:,2)); 
y = R(P(:,1));
plot(x,y,'s','color','white');
% 找出对应的直线边缘
lines = houghlines(I2,T,R,P,'FillGap',5,'MinLength',7);
total = length(lines);  %检测出的直线总数
figure, imshow(I2),hold on;
% sec_line = 0; %秒针长度
% min_line = 0; %分针长度
% hour_line = 0; %时针长度
array0=[];  %存放检测出的直线长度
array1=[];  %排序后的长度

for k = 1:length(lines)
   xy = [lines(k).point1; lines(k).point2];
   plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green');
   % 标记直线边缘对应的起点
   plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');
   plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');
   % 计算直线边缘长度
   len = norm(lines(k).point1 - lines(k).point2);
   array0(k)=len;
end
%按长度排序,降序排列，前三个数分别是秒针长度、分针长度、时针长度
array1 = sort(array0,'descend');
%找到秒针、分针、时针对应的直线，并算出斜率、角度
for k=1:length(lines)
    xy = [lines(k).point1; lines(k).point2];
    len = norm(lines(k).point1 - lines(k).point2);
    if(len == array1(1))
        sec_line = xy;
        angle_s = lines(k).theta;    %算出的角度是与Y轴负方向的夹角， X轴正向是右，Y轴正向是向下
%        k_s = (xy(2,2)-xy(1,2))/(xy(2,1)-xy(1,1)) %秒针斜率
    end
    if( len == array1(2))
        min_line = xy;
        angle_m = lines(k).theta;
%         k_m = (xy(2,2)-xy(1,2))/(xy(2,1)-xy(1,1))
    end
    if(len  == array1(3))
        hour_line = xy;
        angle_h = lines(k).theta;
%         k_h = (xy(2,2)-xy(1,2))/(xy(2,1)-xy(1,1))
    end      
end
  
%highlight the longest line segment
%plot(xy_long(:,1),xy_long(:,2),'LineWidth',2,'Color','blue')
plot(sec_line(:,1),sec_line(:,2),'LineWidth',2,'Color','b');
plot(min_line(:,1),min_line(:,2),'LineWidth',2,'Color','c');
plot(hour_line(:,1),hour_line(:,2),'LineWidth',2,'Color','r');

%转换成常用的xy坐标系
if(angle_m < 0)
    angle_m= -angle_m + 90;
else
    angle_m = 90 - angle_m;
end

if(angle_h < 0)
    angle_h = -angle_h + 90;
else
    angle_h = 90 - angle_h;
end

if(angle_s < 0)
    angle_s = -angle_s + 90;
else
    angle_s = 90 - angle_s;
end



  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 蔡利梅.MATLAB图像处理——理论、算法与实例分析[M].清华大学出版社，2020.
[2]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社，2013.
[3]周品.MATLAB图像处理与图形用户界面设计[M].清华大学出版社，2013.
[4]刘成龙.精通MATLAB图像处理[M].清华大学出版社，2015.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/118302024