【风电功率预测】基于matlab粒子群算法优化LSTM风电功率预测【含Matlab源码 941期】

一、粒子群算法及LSTM简介

1 粒子群算法简介
1.1 粒子群算法的概念**
粒子群优化算法(PSO：Particle swarm optimization) 是一种进化计算技术（evolutionary computation）。源于对鸟群捕食的行为研究。粒子群优化算法的基本思想：是通过群体中个体之间的协作和信息共享来寻找最优解．
PSO的优势：在于简单容易实现并且没有许多参数的调节。目前已被广泛应用于函数优化、神经网络训练、模糊系统控制以及其他遗传算法的应用领域。

1.2 粒子群算法分析
1.2.1基本思想
粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子在搜索空间中单独的搜寻最优解，并将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的那个个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。下面的动图很形象地展示了PSO算法的过程：

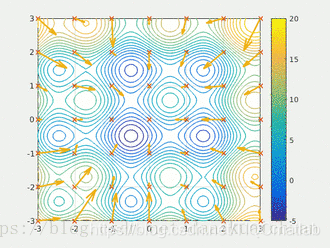
1.2.2 更新规则
PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次的迭代中，粒子通过跟踪两个“极值”(pbest，gbest)来更新自己。在找到这两个最优值后，粒子通过下面的公式来更新自己的速度和位置。

公式(1)的第一部分称为【记忆项】，表示上次速度大小和方向的影响；公式(1)的第二部分称为【自身认知项】，是从当前点指向粒子自身最好点的一个矢量，表示粒子的动作来源于自己经验的部分；公式(1)的第三部分称为【群体认知项】，是一个从当前点指向种群最好点的矢量，反映了粒子间的协同合作和知识共享。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。以上面两个公式为基础，形成了PSO的标准形式。

公式(2)和 公式(3)被视为标准PSO算法。
1.2.3 PSO算法的流程和伪代码

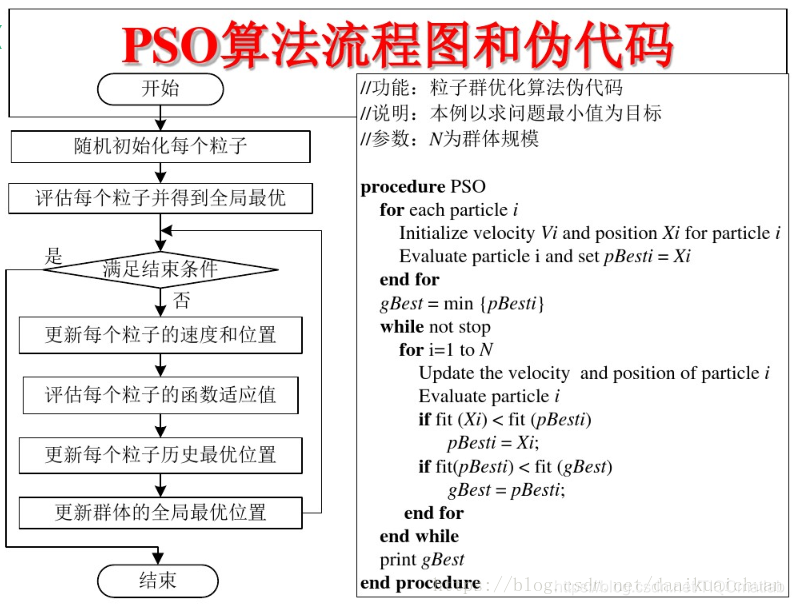
2 LSTM简介
2.1 LSTM控制流程
LSTM的控制流程：是在前向传播的过程中处理流经细胞的数据，不同之处在于 LSTM 中细胞的结构和运算有所变化。

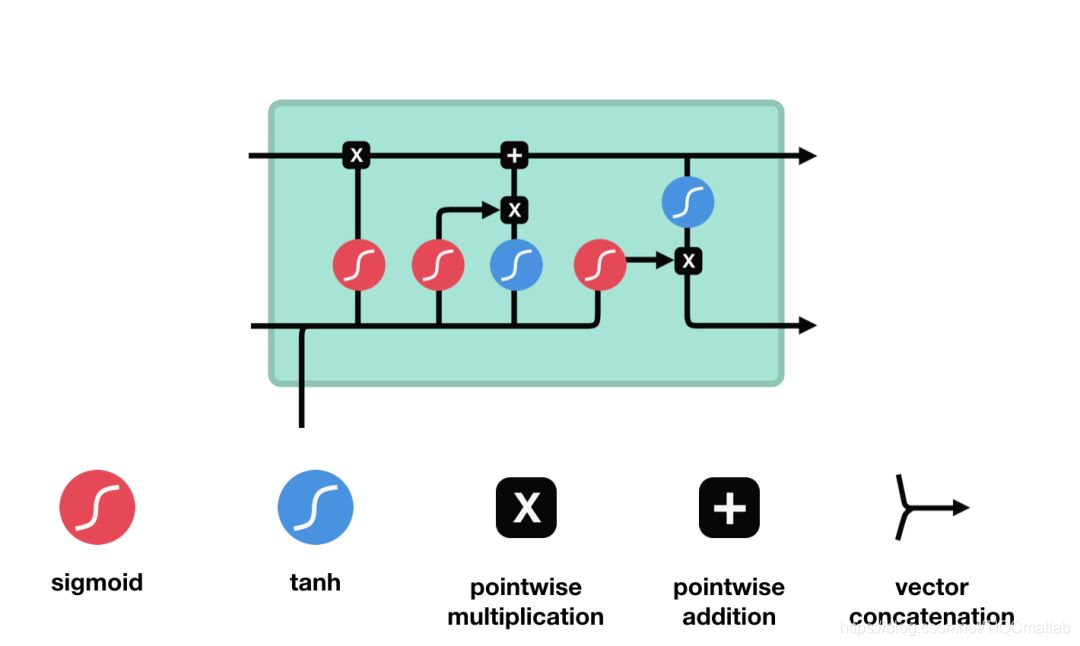
这一系列运算操作使得 LSTM具有能选择保存信息或遗忘信息的功能。咋一看这些运算操作时可能有点复杂，但没关系下面将带你一步步了解这些运算操作。

2.2 核心概念
LSTM 的核心概念在于细胞状态以及“门”结构。细胞状态相当于信息传输的路径，让信息能在序列连中传递下去。你可以将其看作网络的“记忆”。理论上讲，细胞状态能够将序列处理过程中的相关信息一直传递下去。
因此，即使是较早时间步长的信息也能携带到较后时间步长的细胞中来，这克服了短时记忆的影响。信息的添加和移除我们通过“门”结构来实现，“门”结构在训练过程中会去学习该保存或遗忘哪些信息。

2.3 Sigmoid
门结构中包含着 sigmoid 激活函数。Sigmoid 激活函数与 tanh 函数类似，不同之处在于 sigmoid 是把值压缩到 0~1 之间而不是 -1~1 之间。这样的设置有助于更新或忘记信息，因为任何数乘以 0 都得 0，这部分信息就会剔除掉。同样的，任何数乘以 1 都得到它本身，这部分信息就会完美地保存下来。这样网络就能了解哪些数据是需要遗忘，哪些数据是需要保存。

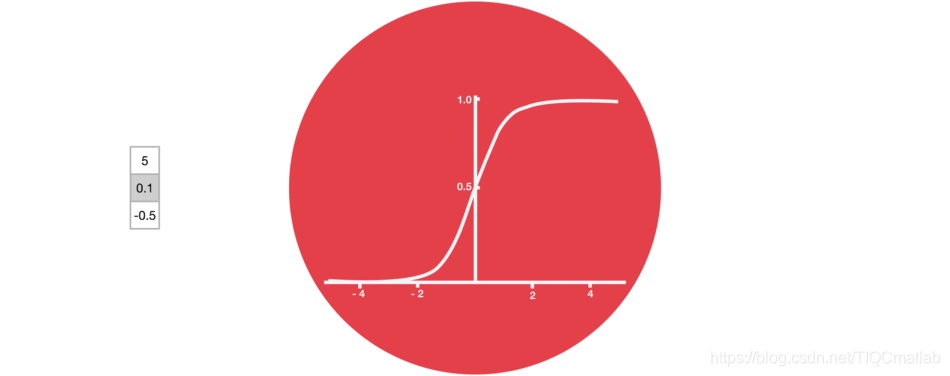
2.4 LSTM门结构
LSTM 有三种类型的门结构：遗忘门、输入门和输出门。
2.4.1 遗忘门
遗忘门的功能是决定应丢弃或保留哪些信息。来自前一个隐藏状态的信息和当前输入的信息同时传递到 sigmoid 函数中去，输出值介于 0 和 1 之间，越接近 0 意味着越应该丢弃，越接近 1 意味着越应该保留。

2.4.2 输入门
输入门用于更新细胞状态。首先将前一层隐藏状态的信息和当前输入的信息传递到 sigmoid 函数中去。将值调整到 0~1 之间来决定要更新哪些信息。0 表示不重要，1 表示重要。
其次还要将前一层隐藏状态的信息和当前输入的信息传递到 tanh 函数中去，创造一个新的侯选值向量。最后将 sigmoid 的输出值与 tanh 的输出值相乘，sigmoid 的输出值将决定 tanh 的输出值中哪些信息是重要且需要保留下来的。

2.4.3 细胞状态
下一步，就是计算细胞状态。首先前一层的细胞状态与遗忘向量逐点相乘。如果它乘以接近 0 的值，意味着在新的细胞状态中，这些信息是需要丢弃掉的。然后再将该值与输入门的输出值逐点相加，将神经网络发现的新信息更新到细胞状态中去。至此，就得到了更新后的细胞状态。

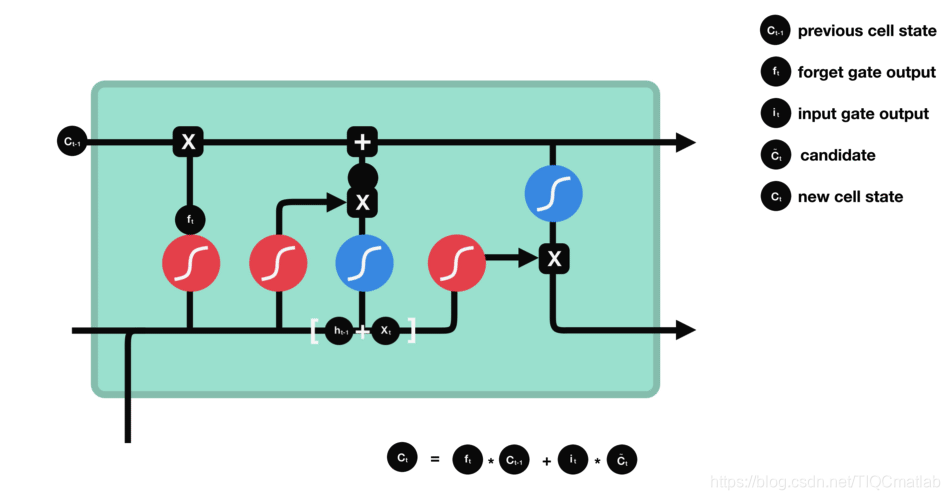
2.4.4 输出门
输出门用来确定下一个隐藏状态的值，隐藏状态包含了先前输入的信息。首先，我们将前一个隐藏状态和当前输入传递到 sigmoid 函数中，然后将新得到的细胞状态传递给 tanh 函数。
最后将 tanh 的输出与 sigmoid 的输出相乘，以确定隐藏状态应携带的信息。再将隐藏状态作为当前细胞的输出，把新的细胞状态和新的隐藏状态传递到下一个时间步长中去。

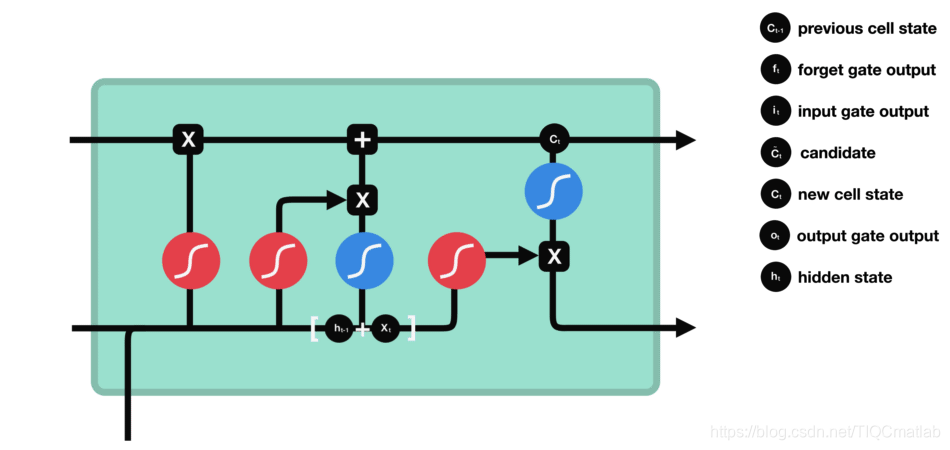
让我们再梳理一下。遗忘门确定前一个步长中哪些相关的信息需要被保留；输入门确定当前输入中哪些信息是重要的，需要被添加的；输出门确定下一个隐藏状态应该是什么。

二、部分源代码

%%%% 基于粒子群算法优化lstm预测单序列
clc
clear all
close all
%加载数据，重构为行向量
%加载数据，重构为行向量
data =xlsread('台风日数据2','Sheet1','B2:E481');%把你的负荷数据赋值给data变量就可以了。

%%

%序列的前 90% 用于训练，后 10% 用于测试
numTimeStepsTrain =round(0.8*size(data,1));
dataTrain = data(1:numTimeStepsTrain,:)';
dataTest = data(numTimeStepsTrain+1:end-1,:)';
numTimeStepsTest = size(data,1)-numTimeStepsTrain-1 ;%步数
%%  数据归一化
[dataTrainStandardized, ps_input] = mapminmax(dataTrain,0,1);
[dataTestStandardized, ps_output] = mapminmax(dataTest,0,1);
%输入LSTM的时间序列交替一个时间步
XTrain = dataTrainStandardized(2:end,:);
YTrain = dataTrainStandardized(1,:);
[dataTrainStandardized_zong, ps_input_zong] = mapminmax(data',0,1);
XTest_zong = dataTrainStandardized_zong(2:end,end);%测试集输入
YTest_zong = dataTest(1,1)';%测试集输出
XTest = dataTestStandardized(2:end,:);%测试集输入
YTest = dataTest(1,:)';%测试集输出
%%
%创建LSTM回归网络，指定LSTM层的隐含单元个数96*3
%序列预测，因此，输入一维，输出一维
numFeatures = 3;%输入层数
numResponses = 1;%输出层数
numHiddenUnits = 20*3;

layers = [ ...
    sequenceInputLayer(numFeatures)
    lstmLayer(numHiddenUnits)
    fullyConnectedLayer(numResponses)
    regressionLayer];
%% 初始化种群
N = 5;                         % 初始种群个数
d = 1;                          % 空间维数
ger =100;                      % 最大迭代次数
limit = [0.001, 0.01;];                % 设置位置参数限制(矩阵的形式可以多维)
vlimit = [-0.005, 0.005;];               % 设置速度限制
c_1 = 0.8;                        % 惯性权重
c_2 = 0.5;                       % 自我学习因子
c_3 = 0.5;                       % 群体学习因子
for i = 1:d
    x(:,i) = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, 1);%初始种群的位置
end
v = 0.005*rand(N, d);                  % 初始种群的速度
xm = x;                          % 每个个体的历史最佳位置
ym = zeros(1, d);                % 种群的历史最佳位置
fxm = 1000*ones(N, 1);               % 每个个体的历史最佳适应度
fym = 1000;                      % 种群历史最佳适应度
%% 粒子群工作
iter = 1;
times = 1;
record = zeros(ger, 1);          % 记录器
while iter <= ger
    iter
    for i=1:N
                %指定训练选项，求解器设置为adam， 250 轮训练。
        %梯度阈值设置为 1。指定初始学习率 0.005，在 125 轮训练后通过乘以因子 0.2 来降低学习率。
        options = trainingOptions('adam', ...
            'MaxEpochs',250, ...
            'GradientThreshold',1, ...
            'InitialLearnRate',x(i,:), ...
            'LearnRateSchedule','piecewise', ...
            'LearnRateDropPeriod',125, ...
            'LearnRateDropFactor',0.1, ...
            'Verbose',0);
        %训练LSTM
        net = trainNetwork(XTrain,YTrain,layers,options);%训练网络
        net = resetState(net);
        net = predictAndUpdateState(net,XTrain);%
        YPred1 = [];
        
        for mm = 1:numTimeStepsTest
            [net,YPred1(:,mm)] = predictAndUpdateState(net,XTest(:,mm),'ExecutionEnvironment','cpu');%%预测
        end
        mint=ps_output.xmin(1);
        maxt=ps_output.xmax(1);
        YPred=postmnmx(YPred1,mint,maxt);%反归一化
        
        for mm = 1:numTimeStepsTest
            
            if dataTest(2,mm)>25
                YPred(mm)=0;
            end
        end
        
        %使用先前计算的参数对预测去标准化。
        %计算均方根误差 (RMSE)。
        
        rmse = sqrt(mean((YPred-YTest').^2));%均方差
        fx(i) = rmse ; % 个体当前适应度
    end
    for i = 1:N
        if fxm(i) > fx(i)
            fxm(i) = fx(i);     % 更新个体历史最佳适应度
            xm(i,:) = x(i,:);   % 更新个体历史最佳位置
            YPred_best1=YPred;
        end
    end
    if fym > min(fxm)
        [fym, nmax] = min(fxm);   % 更新群体历史最佳适应度
        ym = xm(nmax, :);      % 更新群体历史最佳位置
        YPred_best=YPred_best1;
    end
    %%
clc
clear all
close all
%加载数据，重构为行向量
data =xlsread('台风日数据2','Sheet1','B2:E481');%把你的负荷数据赋值给data变量就可以了。

%%

%序列的前 90% 用于训练，后 10% 用于测试
numTimeStepsTrain =round(0.8*size(data,1));
dataTrain = data(1:numTimeStepsTrain,:)';
dataTest = data(numTimeStepsTrain+1:end-1,:)';
        numTimeStepsTest = size(data,1)-numTimeStepsTrain-1 ;%步数
%%  数据归一化
[dataTrainStandardized, ps_input] = mapminmax(dataTrain,0,1);
[dataTestStandardized, ps_output] = mapminmax(dataTest,0,1);
%输入LSTM的时间序列交替一个时间步
XTrain = dataTrainStandardized(2:end,:);
YTrain = dataTrainStandardized(1,:);
[dataTrainStandardized_zong, ps_input_zong] = mapminmax(data',0,1);
XTest_zong = dataTrainStandardized_zong(2:end,end);%测试集输入
YTest_zong = dataTest(1,1)';%测试集输出
XTest = dataTestStandardized(2:end,:);%测试集输入
YTest = dataTest(1,:)';%测试集输出

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
 

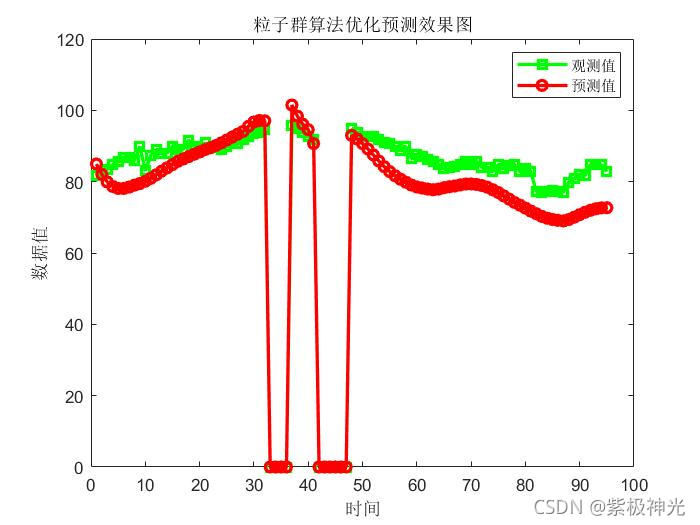
三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/117366295