【BP数据预测】基于matlab粒子群算法优化BP神经网络数据预测（多输入多输出）【含Matlab源码 1418期】

一、粒子群算法及BP神经网络简介

由于BP神经网络在应用过程中初始权值和阈值随机选取,容易出现局部收敛极小点,从而降低拟合效果,为了解决这个问题,采用PSO优化BP神经网络(PSO-BP)算法的初始权值和阈值,解决局部极小点问题,提高BP神经网络算法的预测精度。在PSO中,整个搜索空间的维数D。第i个粒子的位置见式(3)。



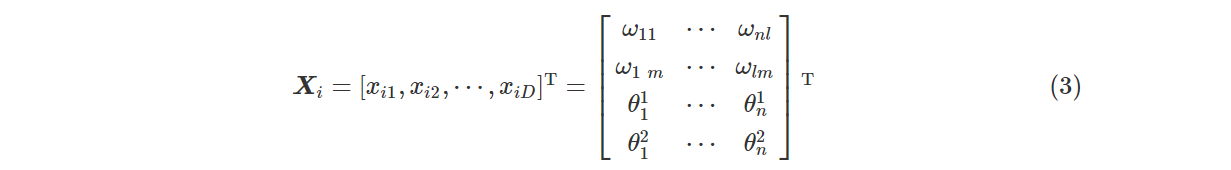
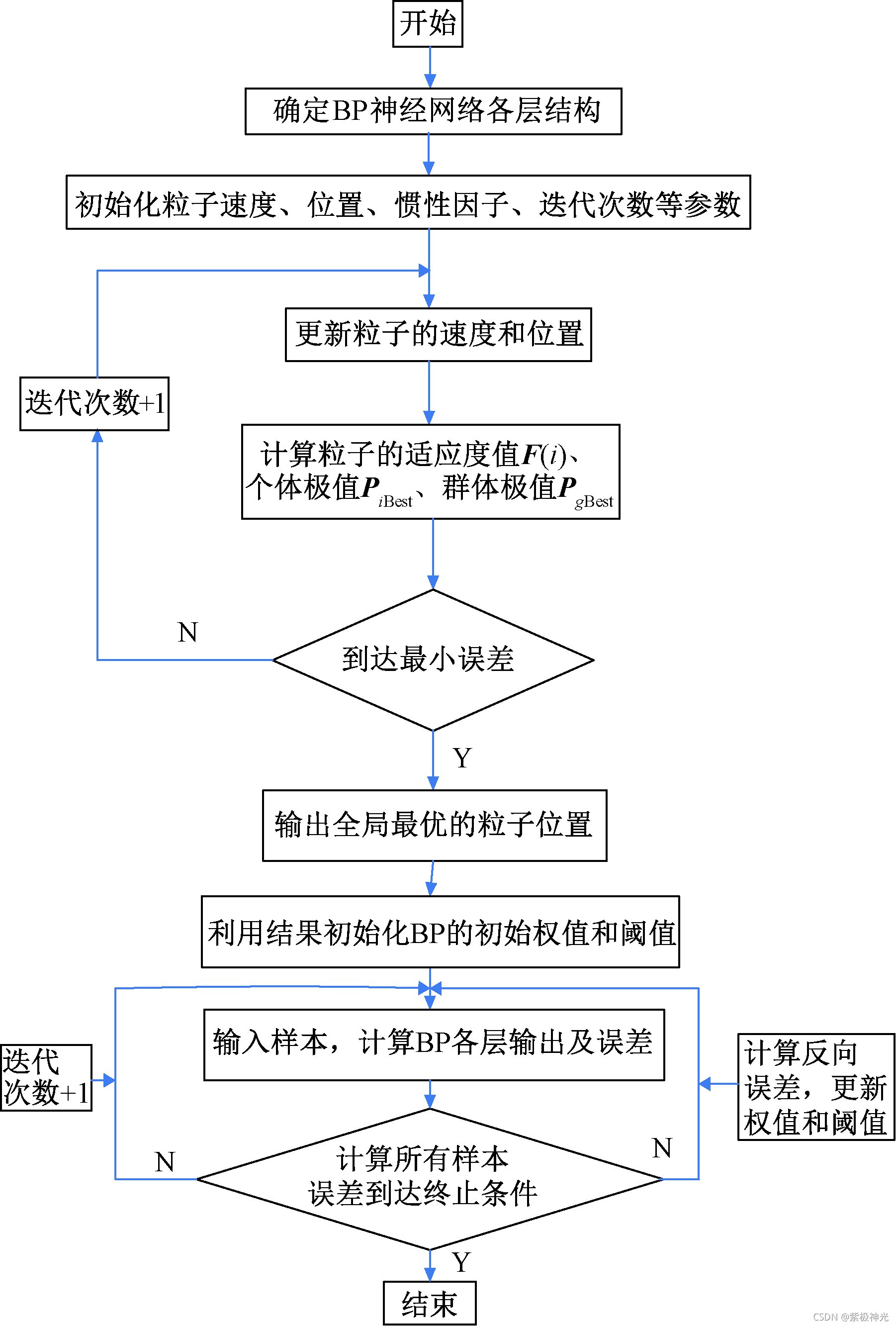
图2 PSO-BP的算法流程

二、部分源代码

%粒子群优化多输入多输出BP神经网络代码
clear
clc
tic
global SamIn SamOut HiddenUnitNum InDim OutDim TrainSamNum
%% 导入训练数据
data = xlsread('data.xlsx');
[data_m,data_n] = size(data);%获取数据维度

P = 80;  %百分之P的数据用于训练，其余测试
Ind = floor(P * data_m / 100);

train_data = data(1:Ind,1:4)';
train_result = data(1:Ind,6:7)';

%% 初始化参数
[InDim,TrainSamNum] = size(train_data);% 学习样本数量
[OutDim,TrainSamNum] = size(train_result);
HiddenUnitNum = 8;                     % 隐含层神经元个数

[SamIn,PS_i] = mapminmax(train_data,0,1);    % 原始样本对（输入和输出）初始化
[SamOut,PS_o] = mapminmax(train_result,0,1);

W1 = HiddenUnitNum*InDim;      % 初始化输入层与隐含层之间的权值
B1 = HiddenUnitNum;          % 初始化输入层与隐含层之间的阈值
W2 = OutDim*HiddenUnitNum;     % 初始化输出层与隐含层之间的权值
B2 = OutDim;                % 初始化输出层与隐含层之间的阈值
L = W1+B1+W2+B2;        %粒子维度

%% *********初始化
M=100;  %种群规模
%初始化粒子位置
X=rand(M,L);
c1=2;  %学习因子
c2=2;
wmax=0.9;%最大最小惯性权重

v=zeros(M,L);%初始化速度
%*******全局最优粒子位置初始化
fmin=inf;
for i=1:M
  
    if fx<fmin
        fmin=fx;
        gb=X(i,:);
    end
end
%********粒子个体历史最优位置初始化
pb=X; 
%********算法迭代
for t=1:Tmax
    w(t)=wmax-(wmax-wmin)*t/Tmax;  %线性下降惯性权重
    for i=1:M
       %******更新粒子速度
       v(i,:)=w(t)*v(i,:)+c1*rand(1)*(pb(i,:)-X(i,:))+c2*rand(1)*(gb-X(i,:));
       if sum(abs(v(i,:)))>1e3
           v(i,:)=rand(size(v(i,:)));
       end
       %*******更新粒子位置
       X(i,:)=X(i,:)+v(i,:);
    end
    %更新pbest和gbest
    for i=1:M
    
        end
        if f(X(i,:))<f(gb)
            gb=X(i,:);
        end
    end
    %保存最佳适应度
    re(t)=f(gb);
    fprintf('经%d次训练，误差为%f，用时%fs\n\n',t,f(gb),toc);
    %可视化迭代过程
    subplot(221)
    plot(gb)
    title('权阈值更新曲线')
    hold on
    subplot(222)
    mesh(v)

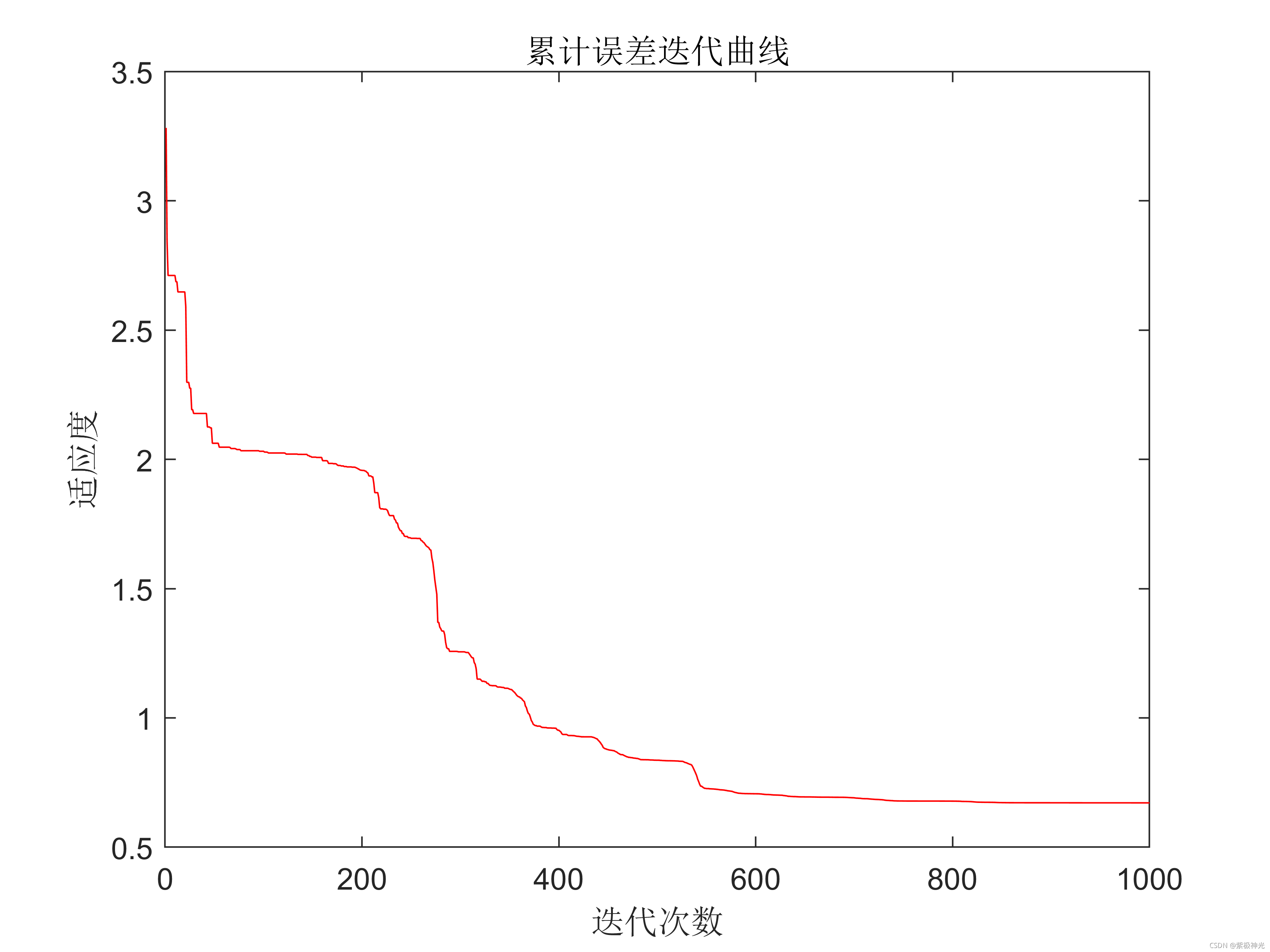
    plot(re,'r')
    title('累计误差迭代曲线')
    img =gcf;  %获取当前画图的句柄
print(img, '-dpng', '-r600', './img4.png')         %即可得到对应格式和期望dpi的图像
    %74-86会增加程序运行时间，注释掉可加快程序运行
end
x = gb;
W1 = x(1:HiddenUnitNum*InDim);

W1 = reshape(W1,[HiddenUnitNum, InDim]);
B1 = x(L1+1:L1+HiddenUnitNum)';
L2 = L1 + length(B1);
W2 = x(L2+1:L2+OutDim*HiddenUnitNum);
L3 = L2 + length(W2);
W2 = reshape(W2,[OutDim, HiddenUnitNum]);
B2 = x(L3+1:L3+OutDim)';


%% 绘制结果
figure
plot(re,'r')
xlabel('迭代次数')
ylabel('适应度')
title('累计误差迭代曲线')
img =gcf;  %获取当前画图的句柄
print(img, '-dpng', '-r600', './img1.png')         %即可得到对应格式和期望dpi的图像
figure
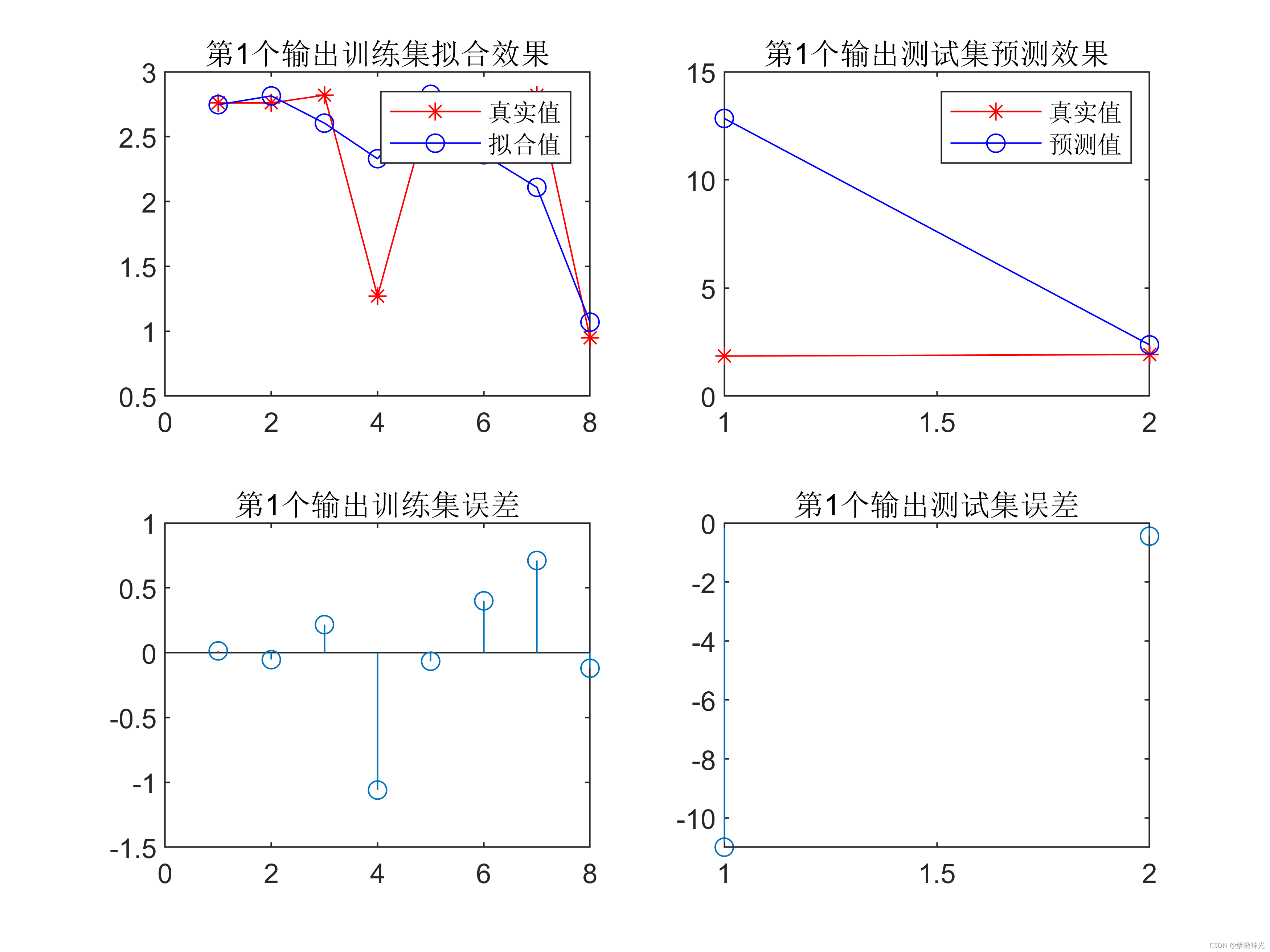
subplot(2,2,1);
plot(train_result(1,:), 'r-*')
hold on
plot(Forcast_data(1,:), 'b-o');
legend('真实值','拟合值')
title('第1个输出训练集拟合效果')
subplot(2,2,2);
plot(test_result(1,:), 'r-*')
hold on
plot(Forcast_data_test(1,:), 'b-o');
legend('真实值','预测值')
title('第1个输出测试集预测效果')
subplot(2,2,3);
stem(train_result(1,:) - Forcast_data(1,:))
title('第1个输出训练集误差')
subplot(2,2,4);
stem(test_result(1,:) - Forcast_data_test(1,:))
title('第1个输出测试集误差')
img =gcf;  %获取当前画图的句柄
print(img, '-dpng', '-r600', './img2.png')         %即可得到对应格式和期望dpi的图像
figure
subplot(2,2,1);
plot(train_result(2,:), 'r-*')
hold on
plot(Forcast_data(2,:), 'b-o');
legend('真实值','拟合值')
title('第2个输出训练集拟合效果')
subplot(2,2,2);
plot(test_result(2,:), 'r-*')
hold on
plot(Forcast_data_test(2,:), 'b-o');
legend('真实值','预测值')
title('第2个输出测试集预测效果')
subplot(2,2,3);
stem(train_result(2,:) - Forcast_data(2,:))
title('第2个输出训练集误差')
subplot(2,2,4);
stem(test_result(2,:) - Forcast_data_test(2,:))
title('第2个输出测试集误差')
img =gcf;  %获取当前画图的句柄
print(img, '-dpng', '-r600', './img3.png')         %即可得到对应格式和期望dpi的图像
toc

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
  
144
  
145
  
146
  
147
  
148
  
149
 

三、运行结果

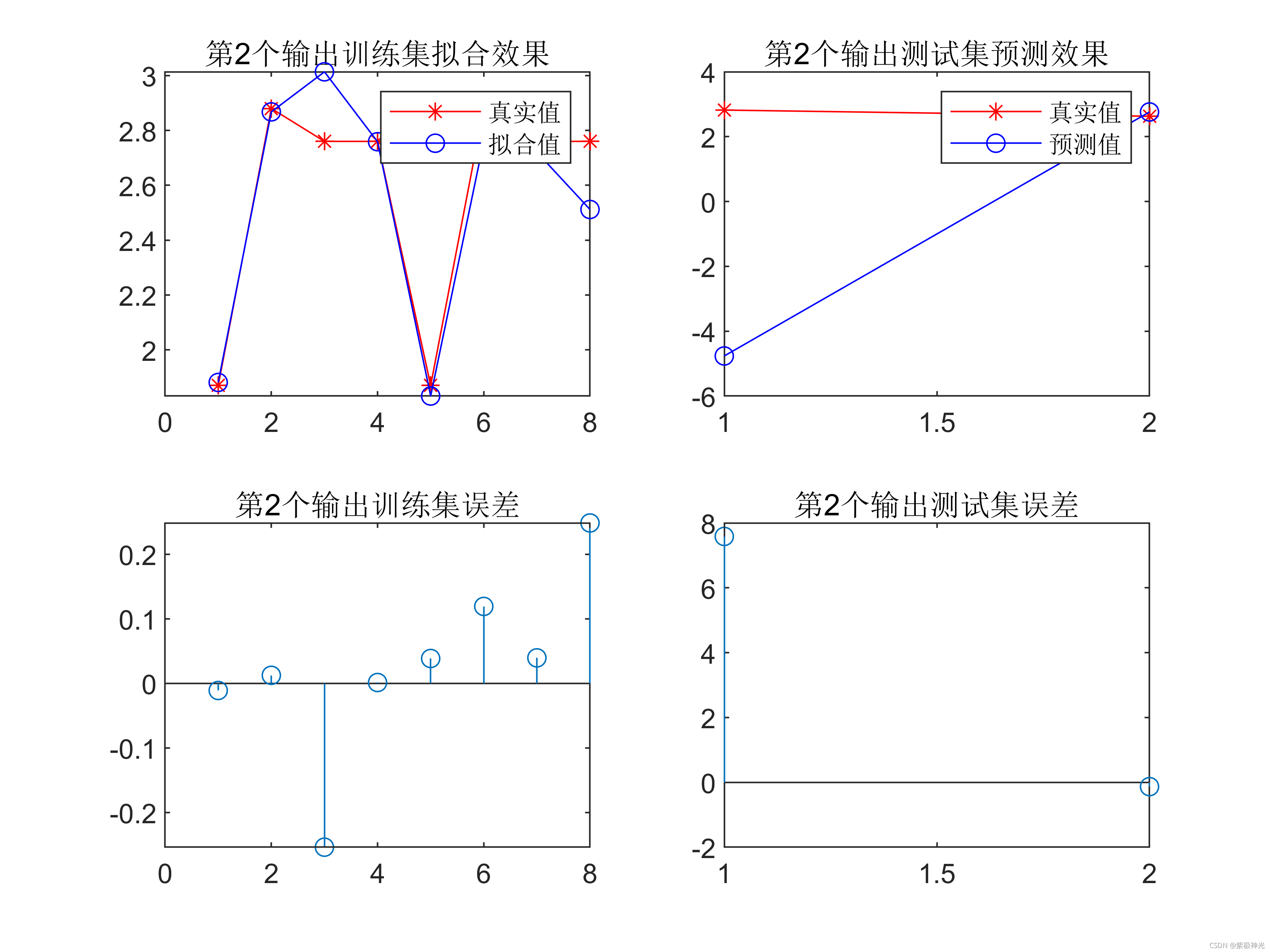
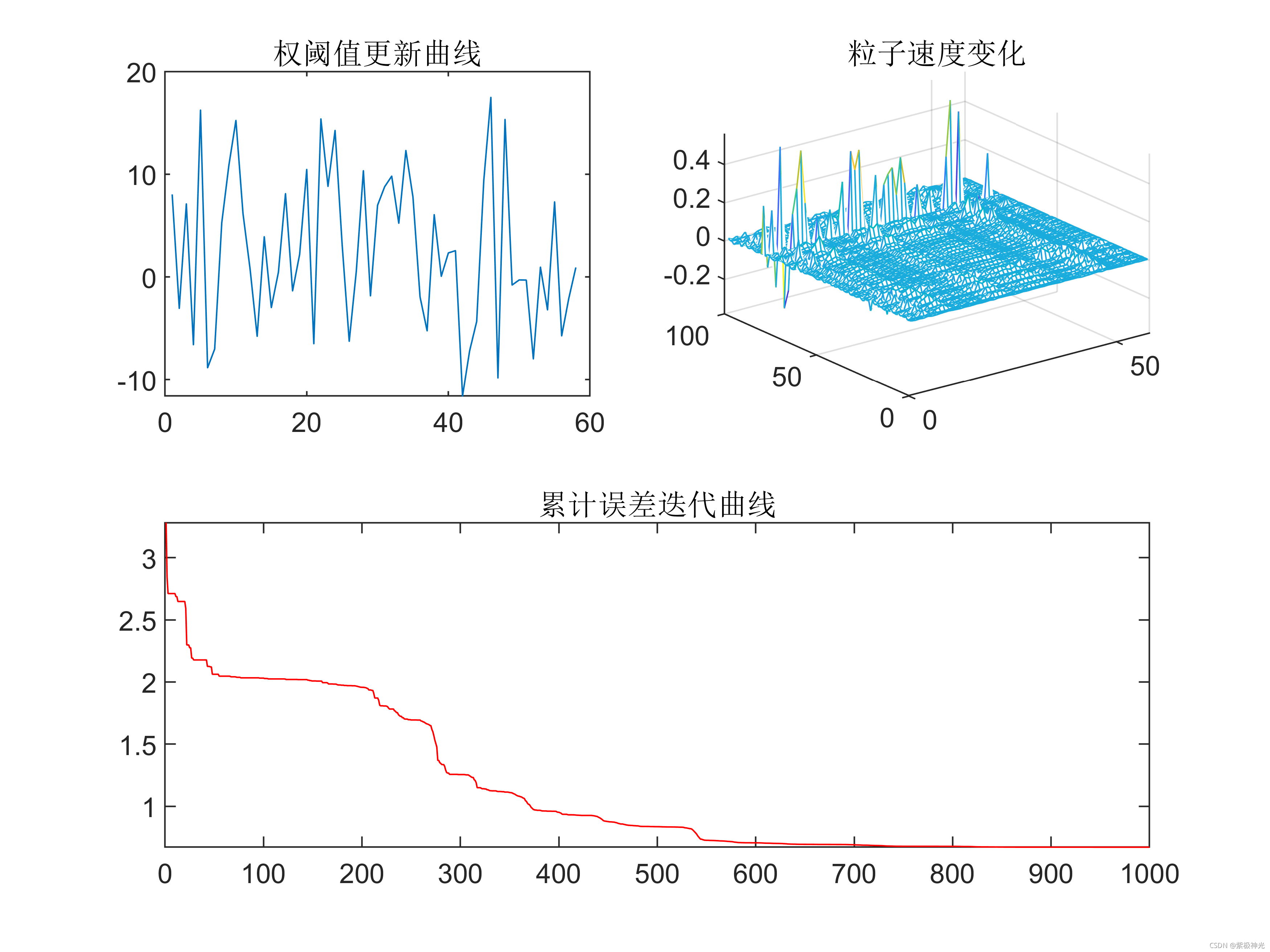
四、matlab版本及参考文献

1 matlab版本
2019b

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.
[6]任圆圆.粒子群优化BP神经网络算法在公路形变预测中的应用分析[J].电子测量技术. 2020,43(12)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/120894331