【单目标优化求解】基于matlab混沌生物地理算法求解单目标问题【含Matlab源码 1411期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源： 【单目标优化求解】基于matlab混沌生物地理算法求解单目标问题【含Matlab源码 1411期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、生物地理算法简介

1 基本思路
BBO 算法起源于生物地理学，它通过模拟多物种在不同栖息地的分布、迁移、突变等规律求解寻优问题，在多目标规划领域有广泛应用. 栖息地被认为是独立的区域，不同的栖息地拥有不同的适宜指数HSI（Habitat suitability index）。 HSI较高的栖息地物种丰富度较高，随着种群趋于饱和，其迁出率增高，迁入率减少，而HIS较低的栖息地与之相反，迁入率增高，迁出率减少. 当栖息地遭遇灾害或瘟疫等突发事件时，HIS将随之突变，打破动态平衡，为低HIS的栖息地添加了不可预见性，增大了搜索目标解的几率2.2 迁移和突变操作物种的迁移有其具体的物理模型，最常的有线性模型、二次模型、余弦模型等 . 以图 3线性模型为例，当某栖息地物种数目为 0 时迁入率最高，此刻 λ = I,随着迁入物种数目不断增加，受阳光、水、食物等资源限制，迁入率不断降低，迁出率不断增高 . 当栖息地物种数目为 S0时，恰好达到动态平衡，此时迁出率与迁入率相同 . 而栖息地达到饱和状态时，物种数量达到最大值Smax ,此刻不再有物种迁入，迁出率 μ = E.突变操作基于生物地理学统计公式完成：


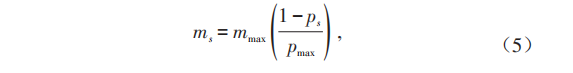
式中：ms为栖息地发生突变的概率，mmax为最大突变率，用户可自行设定 . ps为栖息地容纳s种物种的概率， pmax代表容纳最大种群的概率。

三、部分源代码

clear all
clc

nMonte = 100; % Number of Monte Carlo runs
DisplayFlag = true; % Whether or not to display results during run
GenFlag = true; % whether or not to exit BBO after population becomes uniform
PopSize = 30; % Population sizes for which to run SBBO

% Choose the test function

% ProblemFunction=@Sphere;
% ProblemFunction=@Ackley;
% ProblemFunction=@Fletcher;
% ProblemFunction=@Griewank;
% ProblemFunction=@Penalty1;
% ProblemFunction=@Penalty2;
 ProblemFunction=@Quartic;
% ProblemFunction=@Rastrigin;
% ProblemFunction=@Rosenbrock;
% ProblemFunction=@Schwefel;

% or you objective function
% ProblemFunction=@YourObjectiveFunction;

%Chaotic_map_no=1; %Chebyshev
%Chaotic_map_no=2; %Circle
Chaotic_map_no=3; %Gauss/mouse
%Chaotic_map_no=4; %Iterative
%Chaotic_map_no=5; %Logistic
%Chaotic_map_no=6; %Piecewise
%Chaotic_map_no=7; %Sine
%Chaotic_map_no=8; %Singer
%Chaotic_map_no=9; %Sinusoidal
%Chaotic_map_no=10; %Tent

%You can define the number of search agents and iterations in the Init.m file
Max_iterations=10000;% This should be equal or greater than OPTIONS.Maxgen in Init.m file

ChaosVec=zeros(10,Max_iterations);
%Calculate chaos vector
for i=1:10
    ChaosVec(i,:)=chaos(i,Max_iterations,1);
end

% BBO algorithm
[cg_curve0] = BBO(ProblemFunction, DisplayFlag, PopSize, GenFlag);

% BBO with chaotic selection operator
[cg_curve1] = CBBO1_10(ProblemFunction, DisplayFlag, PopSize, GenFlag,ChaosVec(Chaotic_map_no,:));           

% BBO with chaotic migration operator
[cg_curve2] = CBBO11_20(ProblemFunction, DisplayFlag, PopSize, GenFlag,ChaosVec(Chaotic_map_no,:));           

% BBO with chaotic mutation operator
[cg_curve3] = CBBO21_30(ProblemFunction, DisplayFlag, PopSize, GenFlag,ChaosVec(Chaotic_map_no,:));           

% BBO with chaotic selection/migration operators combined
[cg_curve4] = CBBO31_40(ProblemFunction, DisplayFlag, PopSize, GenFlag,ChaosVec(Chaotic_map_no,:));           

% BBO with chaotic selection/migration/mutation operators combined
[cg_curve5] = CBBO41_50(ProblemFunction, DisplayFlag, PopSize, GenFlag,ChaosVec(Chaotic_map_no,:)); 

semilogy(cg_curve0,'Color','y')
hold on
semilogy(cg_curve1,'Color','k')
semilogy(cg_curve2,'Color','b')
semilogy(cg_curve3,'Color','g')
semilogy(cg_curve4,'Color','r')
semilogy(cg_curve5,'Color','c')

xlabel('Iteration');
ylabel('Best score obtained so far');

axis tight
grid on
box on
legend('BBO' , ['CBBO' num2str(Chaotic_map_no)] , ['CBBO' num2str(Chaotic_map_no+10)] ,['CBBO' num2str(Chaotic_map_no+20)] ,['CBBO' num2str(Chaotic_map_no+30)] ,['CBBO' num2str(Chaotic_map_no+40)] )

function [OPTIONS, MinCost, AvgCost, InitFunction, CostFunction, FeasibleFunction, ...
    MaxParValue, MinParValue, Population] = Init(DisplayFlag, ProblemFunction, RandSeed)

% Initialize population-based optimization software.

% WARNING: some of the optimization routines will not work if population size is odd.
OPTIONS.popsize = 30; % total population size
OPTIONS.Maxgen = 499; % generation count limit
OPTIONS.numVar = 30; % number of genes in each population member
OPTIONS.pmutate = 0; % mutation probability

if ~exist('RandSeed', 'var')
    RandSeed = round(sum(100*clock));
end
%rand('state', RandSeed); % initialize random number generator
if DisplayFlag
    disp(['random # seed = ', num2str(RandSeed)]);
end

% Get the addresses of the initialization, cost, and feasibility functions.
[InitFunction, CostFunction, FeasibleFunction] = ProblemFunction();
% Initialize the population.
[MaxParValue, MinParValue, Population, OPTIONS] = InitFunction(OPTIONS);
% Make sure the population does not have duplicates. 
Population = ClearDups(Population, MaxParValue, MinParValue);
% Compute cost of each individual  
Population = CostFunction(OPTIONS, Population);
% Sort the population from most fit to least fit
Population = PopSort(Population);
% Compute the average cost
AverageCost = ComputeAveCost(Population);
% Display info to screen
MinCost = [Population(1).cost];
AvgCost = [AverageCost];
if DisplayFlag
    disp(['The best and mean of Generation # 0 are ', num2str(MinCost(end)), ' and ', num2str(AvgCost(end))]);
end

return;
function O=chaos(index,max_iter,Value)

O=zeros(1,max_iter);
x(1)=0.7;
switch index
%Chebyshev map
    case 1
for i=1:max_iter
    x(i+1)=cos(i*acos(x(i)));
    G(i)=((x(i)+1)*Value)/2;
end
    case 2
%Circle map
a=0.5;
b=0.2;
for i=1:max_iter
    x(i+1)=mod(x(i)+b-(a/(2*pi))*sin(2*pi*x(i)),1);
    G(i)=x(i)*Value;
end
    case 3
%Gauss/mouse map
for i=1:max_iter
    if x(i)==0
        x(i+1)=0;
    else
        x(i+1)=mod(1/x(i),1);
    end
    G(i)=x(i)*Value;
end

    case 4
%Iterative map
a=0.7;
for i=1:max_iter
    x(i+1)=sin((a*pi)/x(i));
    G(i)=((x(i)+1)*Value)/2;
end

    case 5
%Logistic map
a=4;
for i=1:max_iter
    x(i+1)=a*x(i)*(1-x(i));
    G(i)=x(i)*Value;
end
    case 6
%Piecewise map
P=0.4;
for i=1:max_iter
    if x(i)>=0 && x(i)<P
        x(i+1)=x(i)/P;
    end
    if x(i)>=P && x(i)<0.5
        x(i+1)=(x(i)-P)/(0.5-P);
    end
    if x(i)>=0.5 && x(i)<1-P
        x(i+1)=(1-P-x(i))/(0.5-P);
    end
    if x(i)>=1-P && x(i)<1
        x(i+1)=(1-x(i))/P;
    end    
    G(i)=x(i)*Value;
end

    case 7
%Sine map
for i=1:max_iter
     x(i+1) = sin(pi*x(i));
     G(i)=(x(i))*Value;
 end
    case 8
 %Singer map 
 u=1.07;
 for i=1:max_iter
     x(i+1) = u*(7.86*x(i)-23.31*(x(i)^2)+28.75*(x(i)^3)-13.302875*(x(i)^4));
     G(i)=(x(i))*Value;
 end
    case 9
%Sinusoidal map
 for i=1:max_iter
     x(i+1) = 2.3*x(i)^2*sin(pi*x(i));
     G(i)=(x(i))*Value;
 end
 
    case 10
 %Tent map
 x(1)=0.6;
 for i=1:max_iter
     if x(i)<0.7
         x(i+1)=x(i)/0.7;
     end
     if x(i)>=0.7
         x(i+1)=(10/3)*(1-x(i));
     end
     G(i)=(x(i))*Value;
 end

end
O=G;



  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
  
144
  
145
  
146
  
147
  
148
  
149
  
150
  
151
  
152
  
153
  
154
  
155
  
156
  
157
  
158
  
159
  
160
  
161
  
162
  
163
  
164
  
165
  
166
  
167
  
168
  
169
  
170
  
171
  
172
  
173
  
174
  
175
  
176
  
177
  
178
  
179
  
180
  
181
  
182
  
183
  
184
  
185
  
186
  
187
  
188
  
189
  
190
  
191
  
192
  
193
  
194
  
195
  
196
  
197
  
198
  
199
  
200
  
201
  
202
  
203
  
204
  
205
  
206
  
207
  
208
  
209
  
210
  
211
  
212
  
213
  
214
  
215
  
216
  
217
  
218
  
219
  
220
 

四、运行结果

五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/120858482