【SVM回归预测】基于matlab布谷鸟算法优化SVM回归预测【含Matlab源码 1422期】

一、布谷鸟算法简介

布谷鸟算法，英文叫做Cuckoo search (CS algorithm)。首先还是同样，介绍一下这个算法的英文含义， Cuckoo是布谷鸟的意思，啥是布谷鸟呢，是一种叫做布谷的鸟，o(∩_∩)o ，这种鸟她妈很懒，自己生蛋自己不养，一般把它的宝宝扔到别的种类鸟的鸟巢去。但是呢，当孵化后，遇到聪明的鸟妈妈，一看就知道不是亲生的，直接就被鸟妈妈给杀了。于是这群布谷鸟宝宝为了保命，它们就模仿别的种类的鸟叫，让智商或者情商极低的鸟妈妈误认为是自己的亲宝宝，这样它就活下来了。
布谷鸟搜索算法（Cuckoo Search, CS）是2009年Xin-She Yang 与Suash Deb在《Cuckoo Search via Levy Flights》一文中提出的一种优化算法。布谷鸟算法是一种集合了布谷鸟巢寄生性和莱维飞行（Levy Flights）模式的群体智能搜索技术，通过随机游走的方式搜索得到一个最优的鸟巢来孵化自己的鸟蛋。这种方式可以达到一种高效的寻优模式。

1 布谷鸟的巢寄生性

2 莱维飞行

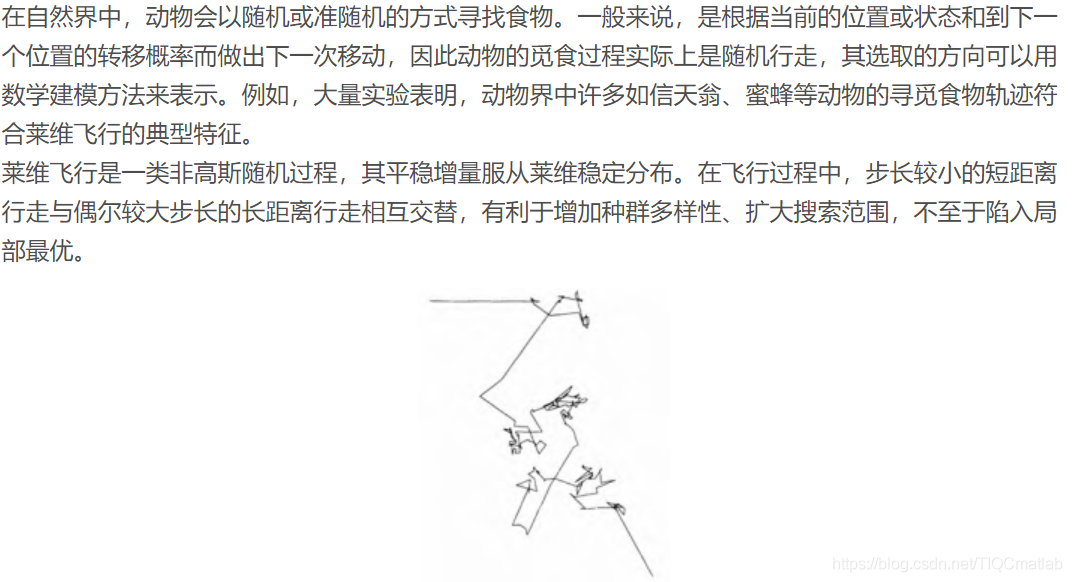
图1.模拟莱维飞行轨迹示意图

3 布谷鸟搜索算法的实现过程

二、部分源代码

%% 数据的提取和预处理                            

% 载入测试数据上证指数(1990.12.19-2009.08.19)
% 数据是一个4579*6的double型的矩阵,每一行表示每一天的上证指数
% 6列分别表示当天上证指数的开盘指数,指数最高值,指数最低值,收盘指数,当日交易量,当日交易额.
clear
clc
load chapter_sh.mat;

% 提取数据
[m,n] = size(sh);
ts = sh(2:m,1);    % 选取2到4579个交易日内每日的开盘指数作为因变量
tsx =sh(1:m-1,:); %选取1到4578个交易日

% 数据预处理,将原始数据进行归一化
ts = ts';
tsx = tsx';

% mapminmax为matlab自带的映射函数	
% 对ts进行归一化
[TS,TSps] = mapminmax(ts,1,2);	%归一化在区间[1 2]
% 对TSX进行转置,以符合libsvm工具箱的数据格式要求
TS = TS';

% mapminmax为matlab自带的映射函数
% 对tsx进行归一化
[TSX,TSXps] = mapminmax(tsx,1,2);	%归一化在区间[1 2]
% 对TSX进行转置,以符合libsvm工具箱的数据格式要求
TSX = TSX';

Tol=1.0e-5;  
n=25;%鸟巢个数
% Discovery rate of alien eggs/solutions
pa=0.25;

                                                          %为最大迭代次数限制
%% Simple bounds of the search domain
% Lower bounds
nd=2; 
Lb=0.01*ones(1,nd); 
% Upper bounds
Ub=100*ones(1,nd);                                                              %随机产生初始解
% Random initial solutions
for i=1:n,      
nest(i,:)=Lb+(Ub-Lb).*rand(size(Lb));
end
%得到当前的最优解
% Get the current best
for i=1:n
    fitness(i)=fun(nest(i,:));
end

fitness=10^10*ones(n,1);
[fmin,bestnest,nest,fitness]=get_best_nest(nest,nest,fitness,Ub,Lb);
for i=1:n
    nest(i,find(nest(i,:)>Ub(1)))=Ub(1);
    nest(i,find(nest(i,:)<Lb(1)))=Lb(1);
end

N_iter=0;                                                                   %开始迭代
%% Starting iterations
for iter=1:1 %while (fmin>Tol),

    % Generate new solutions (but keep the current best)
     new_nest=get_cuckoos(nest,bestnest,Lb,Ub);   
     [fnew,best,nest,fitness]=get_best_nest(nest,new_nest,fitness,Ub,Lb);
    % Update the counter
      N_iter=N_iter+n; 
    % Discovery and randomization
      new_nest=empty_nests(nest,Lb,Ub,pa) ;
    
    % Evaluate this set of solutions
      [fnew,best,nest,fitness]=get_best_nest(nest,new_nest,fitness,Ub,Lb);
    % Update the counter again
      N_iter=N_iter+n;
    % Find the best objective so far  
    if fnew<fmin,
        fmin=fnew;
        bestnest=best;
    end
end %% End of iterations(迭代)

% -----------------------------------------------------------------
% Cuckoo Search (CS) algorithm by Xin-She Yang and Suash Deb      %
% Programmed by Xin-She Yang at Cambridge University              %
% Programming dates: Nov 2008 to June 2009                        %
% Last revised: Dec  2009   (simplified version for demo only)    %
% -----------------------------------------------------------------
% Papers -- Citation Details:
% 1) X.-S. Yang, S. Deb, Cuckoo search via Levy flights,
% in: Proc. of World Congress on Nature & Biologically Inspired
% Computing (NaBIC 2009), December 2009, India,
% IEEE Publications, USA,  pp. 210-214 (2009).
% http://arxiv.org/PS_cache/arxiv/pdf/1003/1003.1594v1.pdf 
% 2) X.-S. Yang, S. Deb, Engineering optimization by cuckoo search,
% Int. J. Mathematical Modelling and Numerical Optimisation, 
% Vol. 1, No. 4, 330-343 (2010). 
% http://arxiv.org/PS_cache/arxiv/pdf/1005/1005.2908v2.pdf
% ----------------------------------------------------------------%
% This demo program only implements a standard version of         %
% Cuckoo Search (CS), as the Levy flights and generation of       %
% new solutions may use slightly different methods.               %
% The pseudo code was given sequentially (select a cuckoo etc),   %
% but the implementation here uses Matlab's vector capability,    %
% which results in neater/better codes and shorter running time.  % 
% This implementation is different and more efficient than the    %
% the demo code provided in the book by 
%    "Yang X. S., Nature-Inspired Metaheuristic Algoirthms,       % 
%     2nd Edition, Luniver Press, (2010).                 "       %
% --------------------------------------------------------------- %

% =============================================================== %
% Notes:                                                          %
% Different implementations may lead to slightly different        %
% behavour and/or results, but there is nothing wrong with it,    %
% as this is the nature of random walks and all metaheuristics.   %
% -----------------------------------------------------------------

function [bestnest,fmin]=cuckoo_search(n)                                   %n为鸟巢数目
if nargin<1, % nargin是用来判断输入变量个数的函数
% Number of nests (or different solutions)
n=25;
end

% Discovery rate of alien eggs/solutions
pa=0.25;

%% Change this if you want to get better results
% Tolerance
Tol=1.0e-5;                                                                 %为最大迭代次数限制
%% Simple bounds of the search domain
% Lower bounds
nd=15; 
Lb=-5*ones(1,nd); 
% Upper bounds
Ub=5*ones(1,nd);
                                                                            %随机产生初始解
% Random initial solutions
for i=1:n,      
nest(i,:)=Lb+(Ub-Lb).*rand(size(Lb));
end
                                                                            %得到当前的最优解
% Get the current best
fitness=10^10*ones(n,1);
[fmin,bestnest,nest,fitness]=get_best_nest(nest,nest,fitness);

N_iter=0;                                                                   %开始迭代
%% Starting iterations
while (fmin>Tol),

    % Generate new solutions (but keep the current best)
     new_nest=get_cuckoos(nest,bestnest,Lb,Ub);   
     [fnew,best,nest,fitness]=get_best_nest(nest,new_nest,fitness);
    % Update the counter
      N_iter=N_iter+n; 
    % Discovery and randomization
      new_nest=empty_nests(nest,Lb,Ub,pa) ;
    
    % Evaluate this set of solutions
      [fnew,best,nest,fitness]=get_best_nest(nest,new_nest,fitness);
    % Update the counter again
      N_iter=N_iter+n;
    % Find the best objective so far  
    if fnew<fmin,
        fmin=fnew;
        bestnest=best;
    end
end %% End of iterations(迭代)

%% Post-optimization processing
%% Display all the nests
disp(strcat('Total number of iterations=',num2str(N_iter)));
fmin
bestnest

%% --------------- All subfunctions are list below ------------------
%% Get cuckoos by ramdom walk
function nest=get_cuckoos(nest,best,Lb,Ub)
% Levy flights
n=size(nest,1);
% Levy exponent and coefficient
% For details, see equation (2.21), Page 16 (chapter 2) of the book
% X. S. Yang, Nature-Inspired Metaheuristic Algorithms, 2nd Edition, Luniver Press, (2010).
beta=3/2;
sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);

for j=1:n,
    s=nest(j,:);
    % This is a simple way of implementing Levy flights
    % For standard random walks, use step=1;
    %% Levy flights by Mantegna's algorithm
    u=randn(size(s))*sigma;
    v=randn(size(s));
    step=u./abs(v).^(1/beta);
  
    % In the next equation, the difference factor (s-best) means that 
    % when the solution is the best solution, it remains unchanged.     
    stepsize=0.01*step.*(s-best);
    % Here the factor 0.01 comes from the fact that L/100 should the typical
    % step size of walks/flights where L is the typical lenghtscale; 
    % otherwise, Levy flights may become too aggresive/efficient, 
    % which makes new solutions (even) jump out side of the design domain 
    % (and thus wasting evaluations).
    % Now the actual random walks or flights
    s=s+stepsize.*randn(size(s));
   % Apply simple bounds/limits
   nest(j,:)=simplebounds(s,Lb,Ub);
end

%% Find the current best nest
function [fmin,best,nest,fitness]=get_best_nest(nest,newnest,fitness)
% Evaluating all new solutions
for j=1:size(nest,1),
    fnew=fobj(newnest(j,:));
    if fnew<=fitness(j),
       fitness(j)=fnew;
       nest(j,:)=newnest(j,:);
    end
end
% Find the current best
[fmin,K]=min(fitness) ;
best=nest(K,:);

%% Replace some nests by constructing new solutions/nests
function new_nest=empty_nests(nest,Lb,Ub,pa)
% A fraction of worse nests are discovered with a probability pa
n=size(nest,1);
% Discovered or not -- a status vector
K=rand(size(nest))>pa;

% In the real world, if a cuckoo's egg is very similar to a host's eggs, then 
% this cuckoo's egg is less likely to be discovered, thus the fitness should 
% be related to the difference in solutions.  Therefore, it is a good idea 
% to do a random walk in a biased way with some random step sizes.  
%% New solution by biased/selective random walks
stepsize=rand*(nest(randperm(n),:)-nest(randperm(n),:));
new_nest=nest+stepsize.*K;

% Application of simple constraints
function s=simplebounds(s,Lb,Ub)
  % Apply the lower bound
  ns_tmp=s;
  I=ns_tmp<Lb;
  ns_tmp(I)=Lb(I);
  
  % Apply the upper bounds 
  J=ns_tmp>Ub;
  ns_tmp(J)=Ub(J);
  % Update this new move 
  s=ns_tmp;

%% You can replace the following by your own functions
% A d-dimensional objective function
function z=fobj(x)
%% d-dimensional sphere function sum_j=1^d (u_j-1)^2. 
%  with a minimum at (1,1, ...., 1); 
sum=0;
global nd;
for i=1:nd
    sum=sum+x(i)^2;
end
z=sum;


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
  
144
  
145
  
146
  
147
  
148
  
149
  
150
  
151
  
152
  
153
  
154
  
155
  
156
  
157
  
158
  
159
  
160
  
161
  
162
  
163
  
164
  
165
  
166
  
167
  
168
  
169
  
170
  
171
  
172
  
173
  
174
  
175
  
176
  
177
  
178
  
179
  
180
  
181
  
182
  
183
  
184
  
185
  
186
  
187
  
188
  
189
  
190
  
191
  
192
  
193
  
194
  
195
  
196
  
197
  
198
  
199
  
200
  
201
  
202
  
203
  
204
  
205
  
206
  
207
  
208
  
209
  
210
  
211
  
212
  
213
  
214
  
215
  
216
  
217
  
218
  
219
  
220
  
221
  
222
  
223
  
224
  
225
  
226
  
227
  
228
  
229
  
230
  
231
  
232
  
233
  
234
  
235
  
236
  
237
  
238
  
239
  
240
  
241
  
242
  
243
  
244
  
245
  
246
  
247
  
248
  
249
  
250
  
251
  
252
  
253
  
254
  
255
  
256
  
257
  
258
  
259
  
260
  
261
  
262
  
263
  
264
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/120894668