【数字信号去噪】基于matlab小波软阈值+硬阈值+改进阈值数字信号去噪【含Matlab源码 1025期】

一、小波语音降噪简介

对于噪声频谱遍布于语音信号频谱之中的宽带噪声，如果噪声振幅比大部分的语音信号振幅低，则削去低幅度成分也就削去了宽带噪声。基于这种思路，可以在频域中采取中心限幅的方法，即让带噪语音信号通过一限幅滤波器，高幅度频谱可以通过而低幅成分不允许通过，从而实现噪声抑制。需要注意的是中心削波不可避免地要损害语音质量，通常只在频域中进行，而一般不在时域中实施。
小波降噪的原理类似于中心削波法。小波降噪最初是由Donoho和Johnstone提出的， 其主要理论依据是，小波变换具有很强的去数据相关性，它能够使信号的能量在小波域集中在一些大的小波系数中；而噪声的能量却分布于整个小波域内。因此，经小波分解后，信号的小波系数幅值要大于噪声的系数幅值。因此，幅值比较大的小波系数一般以信号为主，而幅值比较小的系数在很大程度上是噪声。于是，采用阈值的办法可以把信号系数保留，而使大部分噪声系数减小至0。小波降噪的具体处理过程为：将含噪信号在各尺度上进行小波分解，设定一个阈值，幅值低于该阈值的小波系数置为0，高于该阈值的小波系数或者完全保
留， 或者做相应的“收缩”(shrinkage) 处理。最后； 将处理后获得的小波系数用逆小波变换进行重构，得到去噪后的信号。
阈值去噪中，阈值函数体现了对超过和低于阈值的小波系数的不同处理策略，是阈值去噪中关键的一步。设w表示小波系数， T为给定阈值， sgn(*) 为符号函数， 常见的阈值函数主要有：

二、部分源代码

clc
clear all
close all
fs = 20e3;                  % 采样频率
fn = 3e3;                   % 固有频率
y0 = 5;                      % 位移常数
g = 0.1;                     % 阻尼系数
T = 0.01;                   % 重复周期
N = 4096;                  % 采样点数
NT = round(fs*T);      % 单周期采样点数
t = 0:1/fs:(N-1)/fs;      % 采样时刻
t0 = 0:1/fs:(NT-1)/fs;  % 单周期采样时刻
K = ceil(N/NT)+1;       % 重复次数
y = [];
for i = 1:K
    y = [y,y0*exp(-g*2*pi*fn*t0).*sin(2*pi*fn*sqrt(1-g^2)*t0)];
end
y = y(1:N);
Yf = fft(y);                % 频谱
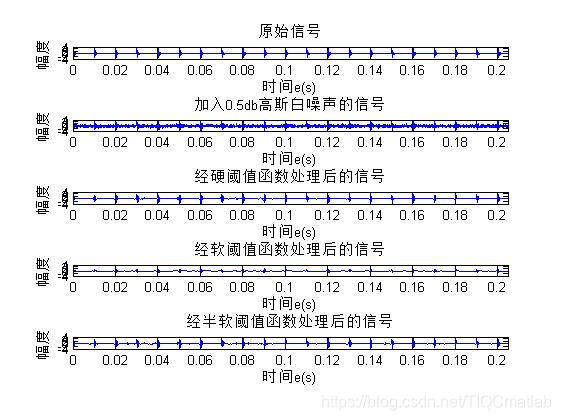
y5 = awgn(y,0.5,'measured'); % Add white Gaussian noise
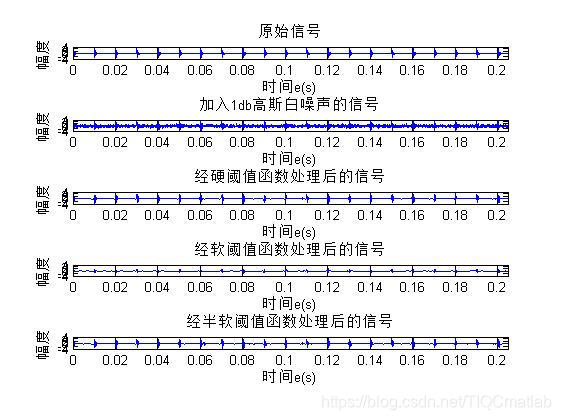
y10 = awgn(y,1,'measured'); % Add white Gaussian noise
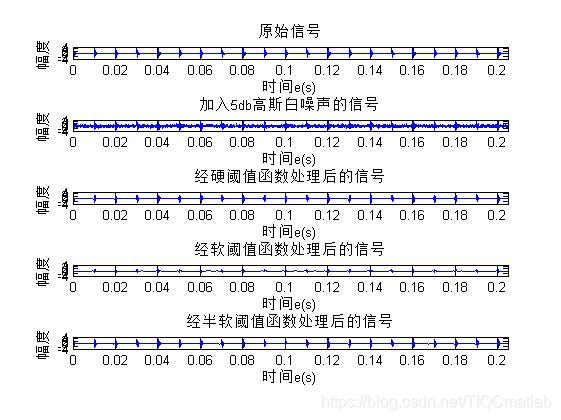
y15 = awgn(y,5,'measured'); % Add white Gaussian noise
%%信噪比=0.5--------------------------------------------

mse12=MSE(y5,xdy12);
PSNR12=PSNR(y5,xdy12);
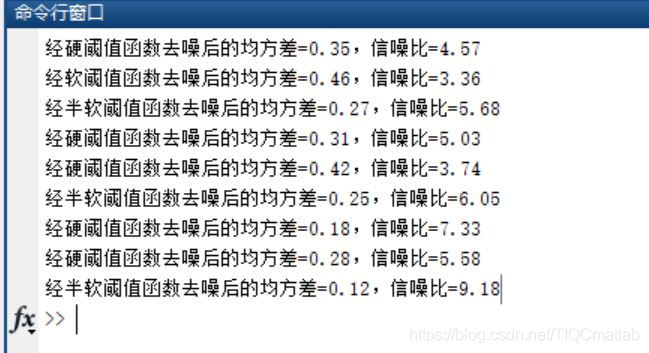
st=sprintf('经软阈值函数去噪后的均方差=%.2f，信噪比=%.2f',mse12,PSNR12);disp(st)

st=sprintf('经半软阈值函数去噪后的均方差=%.2f，信噪比=%.2f',mse13,PSNR13);disp(st)
figure(1);
subplot(511);plot(t,y);axis([0,inf,-4,5]);title('原始信号');xlabel('时间e(s)');ylabel('幅度')
subplot(512);plot(t,y5);axis([0,inf,-4,5]);title('加入0.5db高斯白噪声的信号');xlabel('时间e(s)');ylabel('幅度')
subplot(513);plot(t,xdy11);axis([0,inf,-4,5]);title('经硬阈值函数处理后的信号');xlabel('时间e(s)');ylabel('幅度')
subplot(514);plot(t,xdy12);axis([0,inf,-4,5]);title('经软阈值函数处理后的信号');xlabel('时间e(s)');ylabel('幅度')
subplot(515);plot(t,xdy13);axis([0,inf,-4,5]);title('经半软阈值函数处理后的信号');xlabel('时间e(s)');ylabel('幅度')
function X = denh(x, wname, n, thr)
%硬阈值

[C, S] = wavedec2(x, n, wname);                     %进行小波分解
dcoef = C( prod(S(1, :)) + 1 : end);                %高频部分系数

ind = find( abs(dcoef) < thr) + prod(S(1, :));      %小于阈值thr的系数
C(ind)=0;                                %   直接置零

a=0.6;
ind = find( abs(dcoef) >= thr) + prod(S(1, :));     %大于阈值thr的系数
C(ind) = C(ind);
                                                    %按照公式处理
                                                    function X = denr(x, wname, n, thr)
% 软阈值

[C, S] = wavedec2(x, n, wname);                     %进行小波分解
dcoef = C( prod(S(1, :)) + 1 : end);                %高频部分系数

ind = find( abs(dcoef) < thr) + prod(S(1, :));      %小于阈值thr的系数
C(ind) = 0;                                         %   直接置零

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 沈再阳.精通MATLAB信号处理[M].清华大学出版社，2015.
[2]高宝建,彭进业,王琳,潘建寿.信号与系统——使用MATLAB分析与实现[M].清华大学出版社，2020.
[3]王文光,魏少明,任欣.信号处理与系统分析的MATLAB实现[M].电子工业出版社，2018.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/118034150