【轨迹跟踪】基于matlab无人机轨迹跟踪【含Matlab源码 1152期】
一、L1导航算法简介
L1导航算法是非常经典的非线性无人机路径跟随算法,最早由MIT于2004年提出,其导航算法中是先选点,生成一段为L1的路径。
1 直线路径跟踪

L1路径跟随算法的基本思想就是在期望轨迹上选择一个参考点,并且用这个产生一个横向的加速度,加速度表示为,
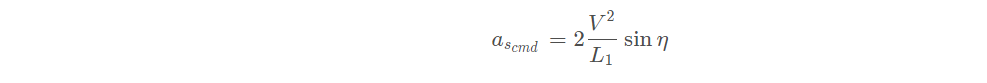
固定翼无人机在横向加速度作用下飞圆弧接近期望轨迹,公式很容易推导,可以看出,加速度与当前空速、空速与L1期望点夹角,以及无人机与L1期望点之间的距离有关。空速可以观测,故横向加速度的求解主要是要确定L1长度,求解η \etaη角。
对于直线期望路径,如下图所示,所求夹角可以表示为,

2 圆弧路径跟踪

圆弧期望加速度求解主要是几何上的一些推导,具体可以看论文中的推导,主要涉及三个角度空速与该点切线的夹角η2 ,该点到L1连线与L1对应弦的夹角η1,2η3相当于是L1所对应于的圆心角。


3 个人对算法的理解
(1)L1轨迹跟踪是非线性的导航算法,在实际的使用中,主要就是要解决L1的取值问题和sin η \sin \etasinη的求解,因为是基于角度正弦的,所以相比于基于偏距的线性算法,在初始偏差比较大的时候,不会出现过激调节,可以比较平滑的向期望路径过渡,而在进入期望路径后,其控制效果较偏距控制更好,尤其是在圆形轨迹跟踪。
(2)L1轨迹跟踪相当于在跟踪一个L1点,这个点的轨迹就是期望路径,点按一定频率刷新,按一定频率计算角度,刷新侧向加速度输出。
(3)对sin η \sin \etasinη进行小角度线性化,可以得到在期望路径附近的加速度线性化的形式,以跟踪直线为例,实际上就是一个二阶系统,
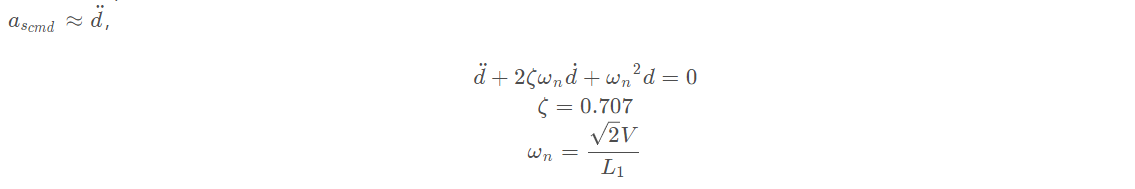
这个二阶系统固有频率和速度以及L1长度有关,阻尼实际上是与那个增益就是那个2倍有关,在论文中,L1取了固定值150m,而V也只测试了25m/s的速度。对于圆的跟踪和直线差不多,只是固有频率也与盘旋半径有关。
二、部分源代码
clc;
clear all;
%% 参考轨迹生成
N=100;
T=0.05;
% Xout=zeros(2*N,3);
% Tout=zeros(2*N,1);
Xout=zeros(N,3);
Tout=zeros(N,1);
for k=1:1:N
Xout(k,1)=k*T;
Xout(k,2)=2;
Xout(k,3)=0;
Tout(k,1)=(k-1)*T;
end
%% Tracking a constant reference trajectory
Nx=3;
Nu =2;
Tsim =20;
X0 = [0 0 pi/3];
[Nr,Nc] = size(Xout); % Nr is the number of rows of Xout
% Mobile Robot Parameters
c = [1 0 0 0;0 1 0 0;0 0 1 0;0 0 0 1];
L = 1;
Rr = 1;
w = 1;
% Mobile Robot variable Model
vd1 = Rr*w; % For circular trajectory
vd2 = 0;
x_real=zeros(Nr,Nc);
x_piao=zeros(Nr,Nc);
u_real=zeros(Nr,2);
u_piao=zeros(Nr,2);
x_real(1,:)=X0;
x_piao(1,:)=x_real(1,:)-Xout(1,:);
X_PIAO=zeros(Nr,Nx*Tsim);
XXX=zeros(Nr,Nx*Tsim);%用于保持每个时刻预测的所有状态值
q=[1 0 0;0 1 0;0 0 0.5];
Q_cell=cell(Tsim,Tsim);
for i=1:1:Tsim
for j=1:1:Tsim
if i==j
Q_cell{i,j}=q;
else
Q_cell{i,j}=zeros(Nx,Nx);
end
end
end
Q=cell2mat(Q_cell);
R=0.1*eye(Nu*Tsim,Nu*Tsim);
for i=1:1:Nr
t_d =Xout(i,3);
a=[1 0 -vd1*sin(t_d)*T;
0 1 vd1*cos(t_d)*T;
0 0 1;];
b=[cos(t_d)*T 0;
sin(t_d)*T 0;
0 T;];
A_cell=cell(Tsim,1);
B_cell=cell(Tsim,Tsim);
for j=1:1:Tsim
A_cell{j,1}=a^j;
for k=1:1:Tsim
if k<=j
B_cell{j,k}=(a^(j-k))*b;
else
B_cell{j,k}=zeros(Nx,Nu);
end
end
end
A=cell2mat(A_cell);
B=cell2mat(B_cell);
b_cons=[];
lb=[-1;-1];
ub=[1;1];
tic
[X,fval(i,1),exitflag(i,1),output(i,1)]=quadprog(H,f,A_cons,b_cons,[],[],lb,ub);
toc
X_PIAO(i,:)=(A*x_piao(i,:)'+B*X)';
if i+j<Nr
for j=1:1:Tsim
XXX(i,1+3*(j-1))=X_PIAO(i,1+3*(j-1))+Xout(i+j,1);
XXX(i,2+3*(j-1))=X_PIAO(i,2+3*(j-1))+Xout(i+j,2);
XXX(i,3+3*(j-1))=X_PIAO(i,3+3*(j-1))+Xout(i+j,3);
end
else
for j=1:1:Tsim
XXX(i,1+3*(j-1))=X_PIAO(i,1+3*(j-1))+Xout(Nr,1);
XXX(i,2+3*(j-1))=X_PIAO(i,2+3*(j-1))+Xout(Nr,2);
XXX(i,3+3*(j-1))=X_PIAO(i,3+3*(j-1))+Xout(Nr,3);
end
end
u_piao(i,1)=X(1,1);
u_piao(i,2)=X(2,1);
Tvec=[0:0.05:4];
X00=x_real(i,:);
vd11=vd1+u_piao(i,1);
vd22=vd2+u_piao(i,2);
XOUT=dsolve('Dx-vd11*cos(z)=0','Dy-vd11*sin(z)=0','Dz-vd22=0','x(0)=X00(1)','y(0)=X00(2)','z(0)=X00(3)');
t=T;
x_real(i+1,1)=eval(XOUT.x);
x_real(i+1,2)=eval(XOUT.y);
x_real(i+1,3)=eval(XOUT.z);
if(i<Nr)
x_piao(i+1,:)=x_real(i+1,:)-Xout(i+1,:);
end
u_real(i,1)=vd1+u_piao(i,1);
u_real(i,2)=vd2+u_piao(i,2);
figure(1);
hold on;
title('跟踪结果对比');
xlabel('横向位置X');
axis([-1 5 -1 3]);
ylabel('纵向位置Y');
hold on;
for k=1:1:Tsim
X(i,k+1)=XXX(i,1+3*(k-1));
Y(i,k+1)=XXX(i,2+3*(k-1));
end
X(i,1)=x_real(i,1);
Y(i,1)=x_real(i,2);
plot(X(i,:),Y(i,:),'y')
hold on;
end
%% 以下为绘图部分
figure(2)
subplot(3,1,1);
hold on;
%grid on;
%title('状态量-横向坐标X对比');
xlabel('采样时间T');
ylabel('横向位置X')
subplot(3,1,2);
plot(Tout(1:Nr),Xout(1:Nr,2),'k--');
hold on;
%grid on;
%title('状态量-横向坐标Y对比');
xlabel('采样时间T');
ylabel('纵向位置Y')
subplot(3,1,3);
hold on;
%grid on;
hold on;
%title('状态量-\theta对比');
xlabel('采样时间T');
ylabel('\theta')
figure(3)
subplot(2,1,1);
%grid on;
%title('控制量-纵向速度v对比');
xlabel('采样时间T');
ylabel('纵向速度')
subplot(2,1,2)
%grid on;
%title('控制量-角加速度对比');
xlabel('采样时间T');
ylabel('角加速度')
figure(4)
subplot(3,1,1);
%grid on;
xlabel('采样时间T');
ylabel('e(x)');
subplot(3,1,2);
%grid on;
xlabel('采样时间T');
ylabel('e(y)');
subplot(3,1,3);
%grid on;
xlabel('采样时间T');
ylabel('e(\theta)');
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
三、运行结果




四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]张萍.四旋翼飞行器姿态控制建模与仿真[J].电机与控制应用. 2019,46(12)
[4]刘岩,杨牧.四旋翼飞行器飞行控制系统研究与设计[J].山东工业技术. 2019,(07)
文章来源: qq912100926.blog.csdn.net,作者:海神之光,版权归原作者所有,如需转载,请联系作者。
原文链接:qq912100926.blog.csdn.net/article/details/119045751
- 点赞
- 收藏
- 关注作者



评论(0)