【PF三维路径规划】基于matlab改进的粒子滤波无人机三维路径规划【含Matlab源码 1269期】
一、无人机简介
0 引言
随着现代技术的发展,飞行器种类不断变多,应用也日趋专一化、完善化,如专门用作植保的大疆PS-X625无人机,用作街景拍摄与监控巡察的宝鸡行翼航空科技的X8无人机,以及用作水下救援的白鲨MIX水下无人机等,决定飞行器性能主要是内部的飞控系统和外部的路径规划问题。就路径问题而言,在具体实施任务时仅靠操作员手中的遥控器控制无人飞行器执行相应的工作,可能会对操作员心理以及技术提出极高的要求,为了避免个人操作失误,进而造成飞行器损坏的危险,一种解决问题的方法就是对飞行器进行航迹规划。
飞行器的测量精度,航迹路径的合理规划,飞行器工作时的稳定性、安全性等这些变化对飞行器的综合控制系统要求越来越高。无人机航路规划是为了保证无人机完成特定的飞行任务,并且能够在完成任务的过程中躲避各种障碍、威胁区域而设计出最优航迹路线的问题。
1 常见的航迹规划算法
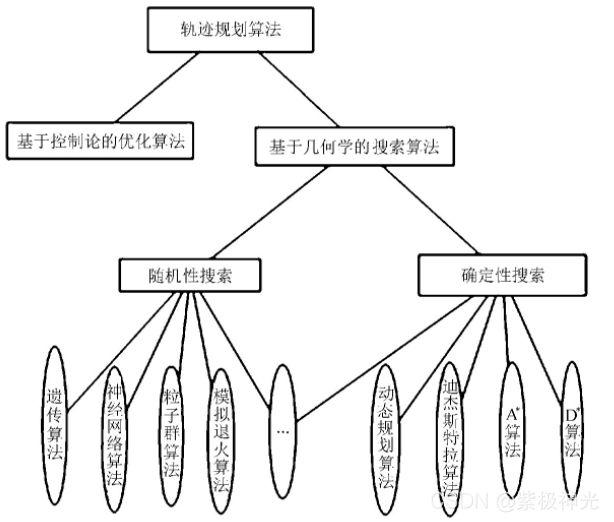
图1 常见路径规划算法
文中主要对无人机巡航阶段的航迹规划进行研究,假设无人机在飞行中维持高度与速度不变,那么航迹规划成为一个二维平面的规划问题。在航迹规划算法中,A算法计算简单,容易实现。在改进A算法基础上,提出一种新的、易于理解的改进A算法的无人机航迹规划方法。传统A算法将规划区域栅格化,节点扩展只限于栅格线的交叉点,在栅格线的交叉点与交叉点之间往往存在一定角度的两个运动方向。将存在角度的两段路径无限放大、细化,然后分别用两段上的相应路径规划点作为切点,找到相对应的组成内切圆的圆心,然后作弧,并求出相对应的两切点之间的弧所对应的圆心角,根据下式计算出弧线的长度
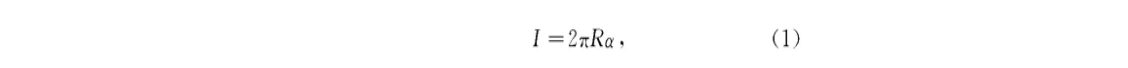
式中:R———内切圆的半径;
α———切点之间弧线对应的圆心角。
二、粒子滤波算法简介
粒子滤波是一种贝叶斯次优估计算法,它摆脱了解决非线性滤波问题时随机量必须 满足高斯分布的制约条件,并在一定程度上解决了粒子样本匮乏问题,因此,近年来该算法在许多领域得到成功应用。 但是,粒子滤波中的粒子退化问题严重地限制了其基本方法 的发展。粒子滤波详见MCMC 改进粒子滤波算法及其在目标跟踪中的应用
三、部分源代码
% 功能说明:ekf,ukf,pf,改进pf算法的无人机航迹预测比较程序
function main
% 因本程序涉及太多的随机数,下面让随机数每次都不变
rand('seed',3);
randn('seed',6);
% error('下面的参数T请参考书中的值设置,然后删除本行代码')
n = 9;
T = 50;
Q= [1 0 0 0 0 0 0 0 0; % 过程噪声协方差矩阵
0 1 0 0 0 0 0 0 0;
0 0 1 0 0 0 0 0 0;
0 0 0 0.01 0 0 0 0 0;
0 0 0 0 0.01 0 0 0 0;
0 0 0 0 0 0.01 0 0 0;
0 0 0 0 0 0 0.0001 0 0;
0 0 0 0 0 0 0 0.0001 0;
0 0 0 0 0 0 0 0 0.0001];
R = [5000 0 0; % 观测噪声协方差矩阵
0 0.01^2 0 % 角度的观测值偏差不能给的太大
0 0 0.01^2];
% 系统初始化
X = zeros(9,T); % 真实值
Z = zeros(3,T);
% 真实状态初始化
%X(:,1)=[1000;5000;200;10;50;10;2;-4;2]+sqrtm(Q)*randn(n,1);
X(:,1)=[100;500;20;10;50;10;2;-4;2]+sqrtm(Q)*randn(n,1);
state0 = X(:,1);
x0=0;
y0=0;
z0=0;
Station=[x0;y0;z0]; % 观测站的位置
P0 =[100 0 0 0 0 0 0 0 0; % 协方差初始化
0 100 0 0 0 0 0 0 0;
0 0 100 0 0 0 0 0 0;
0 0 0 1 0 0 0 0 0;
0 0 0 0 1 0 0 0 0;
0 0 0 0 0 1 0 0 0;
0 0 0 0 0 0 0.1 0 0;
0 0 0 0 0 0 0 0.1 0
0 0 0 0 0 0 0 0 0.1];
%%%%%%%%%%%%% EKF滤波算法 %%%%%%%%%%%%
Qekf = Q; % EKF过程噪声方差
Rekf = R; % EKF过程噪声方差
Xekf=zeros(9,T); % 滤波状态
Xekf(:,1)=X(:,1); % EKF滤波初始化
Pekf = P0; % 协方差
Tekf=zeros(1,T); % 用于记录一个采样周期的算法时间消耗
%%%%%%%%%%%%% UKF滤波算法 %%%%%%%%%%%%
Qukf = Q; % UKF过程噪声方差
Rukf = R; % UKF观测噪声方差
Xukf=zeros(9,T); % 滤波状态
Xukf(:,1)=X(:,1); % UKF滤波初始化
Pukf = P0; % 协方差
Tukf=zeros(1,T); % 用于记录一个采样周期的算法时间消耗
%%%%%%%%%%%%% PF滤波算法 %%%%%%%%%%%%
N = 200; % 粒子数
Xpf=zeros(n,T); % 滤波状态
Xpf(:,1)=X(:,1); % PF滤波初始化
Xpfset=ones(n,N); % 粒子集合初始化
for j=1:N % 粒子集初始化
Xpfset(:,j)=state0; % 全都初始化为x0,每个粒子的值相等
end
Tpf=zeros(1,T); % 用于记录一个采样周期的算法时间消耗
%%%%%%%%%%%%% PF2滤波算法 %%%%%%%%%%%%
N2 = 200; % 粒子数
R2 = [5000 0 0; % 观测噪声协方差矩阵
0 0.01^2 0 % 角度的观测值偏差不能给的太大
0 0 0.01^2];
Xpf2=zeros(n,T); % 滤波状态
Xpf2(:,1)=X(:,1); % PF滤波初始化
Xpf2set=ones(n,N2); % 粒子集合初始化
for j=1:N2 % 粒子集初始化
Xpf2set(:,j)=state0; % 全都初始化为x0,每个粒子的值相等
end
%%%%%%%%%%%%% PF3滤波算法 %%%%%%%%%%%%
N3 = 400; % 粒子数
R3 = [5000 0 0; % 观测噪声协方差矩阵
0 0.01^2 0 % 角度的观测值偏差不能给的太大
0 0 0.01^2];
Xpf3=zeros(n,T); % 滤波状态
Xpf3(:,1)=X(:,1); % PF滤波初始化
Xpf3set=ones(n,N3); % 粒子集合初始化
for j=1:N3 % 粒子集初始化
Xpf3set(:,j)=state0; % 全都初始化为x0,每个粒子的值相等
end
Rekf2 = R2;
Xepf2=zeros(9,T); % 滤波状态
Xepf2(:,1)=X(:,1); % EPF滤波初始化
Xepf2set=ones(n,N2); % 粒子集合初始化,这里需要定义为一个3维数组,或者简单起见,一次性写完,定义为一个(9xN)的二维数组,表示当前状态的所有粒子
for j=1:N2 % 粒子集初始化
Xepf2set(:,j)=state0; % 全都初始化为state0,每个粒子的值相等
end
Pepf2 = P0*ones(n,n*N2);% 各个粒子的协方差,这里需要定义为一个3维数组,或者简单起见,一次性写完,定义为一个9x(9xN)的二维数组
%%%%%%%%%%%%% EPF3滤波算法 %%%%%%%%%%%%
Rekf3 = R3;
Xepf3=zeros(9,T); % 滤波状态
Xepf3(:,1)=X(:,1); % EPF滤波初始化
Xepf3set=ones(n,N3); % 粒子集合初始化,这里需要定义为一个3维数组,或者简单起见,一次性写完,定义为一个(9xN)的二维数组,表示当前状态的所有粒子
for j=1:N3 % 粒子集初始化
Xepf3set(:,j)=state0; % 全都初始化为state0,每个粒子的值相等
end
Pepf3 = P0*ones(n,n*N3);% 各个粒子的协方差,这里需要定义为一个3维数组,或者简单起见,一次性写完,定义为一个9x(9xN)的二维数组
%%%%%%%%%%%%% UPF滤波算法 %%%%%%%%%%%%
Xupf=zeros(n,T); % 滤波状态
Xupf(:,1)=X(:,1); % UPF滤波初始化
Xupfset=ones(n,N); % 粒子集合初始化
for j=1:N % 粒子集初始化
Xupfset(:,j)=state0; % 全都初始化为state0,每个粒子的值相等
end
Pupf = P0*ones(n,n*N); % 各个粒子的协方差
Tupf=zeros(1,T); % 用于记录一个采样周期的算法时间消耗
Xmupf = zeros(n,T); % 滤波状态
Tmupf = zeros(1,T);
%%%%%%%%%%%%%%%%%%%%%% 模拟系统运行 %%%%%%%%%%%%%%%%%%%%%%%%%
for t=2:T
% 模拟系统状态运行一步
[y1,y2,y3,y4,y5,y6,y7,y8,y9] = feval('ffun',X(:,t-1));
X(:,t)= [y1,y2,y3,y4,y5,y6,y7,y8,y9]'+ sqrtm(Q) * randn(n,1); % 产生实际状态值
end
% 模拟目标运动过程,观测站对目标观测获取距离数据
for t=1:T
[dd,alpha,beta]=feval('hfun',X(:,t),Station);
Z(:,t)= [dd,alpha,beta]'+sqrtm(R)*randn(3,1);
end
[Xepf(:,t),Xepfset,Pepf,Neffepf]=epf(Xepfset,Z(:,t),n,Pepf,N,R,Qekf,Rekf,Station); % 搞定
Tepf(t)=toc;
sum_epf = sum_epf + Neffepf;
% 调用EPF2算法
[Xepf2(:,t),Xepf2set,Pepf2,Neffepf]=epf(Xepf2set,Z(:,t),n,Pepf2,N2,R2,Qekf,Rekf2,Station); % 搞定
% 调用EPF3算法
[Xepf3(:,t),Xepf3set,Pepf3,Neffepf]=epf(Xepf3set,Z(:,t),n,Pepf3,N3,R3,Qekf,Rekf3,Station); % 搞定
% 调用UPF算法
%tic
%[Xupf(:,t),Xupfset,Pupf]=upf(Xupfset,Z(:,t),n,Pupf,N,R,Qukf,Rukf,Station); % 1
%Tupf(t)=toc;
end
%%%%%%%%%%%%%%%%%%%%%% 数据分析 %%%%%%%%%%%%%%%%%%%%%%%%%
% 假定
for i = 1:T
Xupf(:,i) = X(:,i) + 2 * sin(t);
end
% RMS偏差比较图
EKFrms = zeros(1,T);
UKFrms = zeros(1,T);
PFrms = zeros(1,T);
EPFrms = zeros(1,T);
PF2rms = zeros(1,T);
EPF2rms = zeros(1,T);
PF3rms = zeros(1,T);
EPF3rms = zeros(1,T);
UPFrms = zeros(1,T);
end
% X轴RMS偏差比较图
EKFXrms = zeros(1,T);
UKFXrms = zeros(1,T);
PFXrms = zeros(1,T);
EPFXrms = zeros(1,T);
% X轴RMS偏差比较图
EKFYrms = zeros(1,T);
UKFYrms = zeros(1,T);
PFYrms = zeros(1,T);
EPFYrms = zeros(1,T);
% Z轴RMS偏差比较图
EKFZrms = zeros(1,T);
UKFZrms = zeros(1,T);
PFZrms = zeros(1,T);
EPFZrms = zeros(1,T);
for t=1:T
EKFXrms(1,t)=abs(X(1,t)-Xekf(1,t));
UKFXrms(1,t)=abs(X(1,t)-Xukf(1,t));
PFXrms(1,t)=abs(X(1,t)-Xpf(1,t));
EPFXrms(1,t)=abs(X(1,t)-Xepf(1,t));
EKFYrms(1,t)=abs(X(2,t)-Xekf(2,t));
UKFYrms(1,t)=abs(X(2,t)-Xukf(2,t));
PFYrms(1,t)=abs(X(2,t)-Xpf(2,t));
EPFYrms(1,t)=abs(X(2,t)-Xepf(2,t));
EKFZrms(1,t)=abs(X(3,t)-Xekf(3,t));
UKFZrms(1,t)=abs(X(3,t)-Xukf(3,t));
PFZrms(1,t)=abs(X(3,t)-Xpf(3,t));
EPFZrms(1,t)=abs(X(3,t)-Xepf(3,t));
end
% 画图,三维轨迹图
NodePostion = [100,800,100;
200,800,900;
0,0,0];
figure
t=1:T;
hold on;
box on;
grid on;
for i=1:3
p8=plot3(NodePostion(1,i),NodePostion(2,i),NodePostion(3,i),'ro','MarkerFaceColor','b');
text(NodePostion(1,i)+0.5,NodePostion(2,i)+0.5,NodePostion(3,i)+1,
figure
hold on;
box on;
p1=plot(1:T,EKFrms,'-k.','lineWidth',2);
p2=plot(1:T,UKFrms,'-m^','lineWidth',2);
p3=plot(1:T,PFrms,'-ro','lineWidth',2);
%p4=plot(1:T,EPFrms,'-g*','lineWidth',2);
p5=plot(1:T,UPFrms,'-bp','lineWidth',2);
legend([p1,p2,p3,p5],'EKF偏差','UKF偏差','PF偏差','DFEPF偏差');
xlabel('time step');
ylabel('RMS预测偏差');
figure;
hold on;
box on;
p1=plot(1:T,PFrms,'-k.','lineWidth',2);
p2=plot(1:T,EPFrms,'-m^','lineWidth',2);
p3=plot(1:T,PF2rms,'-r.','lineWidth',2);
p4=plot(1:T,EPF2rms,'-cp','lineWidth',2);
p5=plot(1:T,PF3rms,'-g.','lineWidth',2);
p6=plot(1:T,EPF3rms,'-bp','lineWidth',2);
legend([p1,p2,p3,p4,p5,p6],'PF偏差(Rc=5R,N=200)','DFEPF偏差(Rc=5R,N=200)','PF偏差(Rc=8R,N=200)','DFEPF偏差(Rc=8R,N=200)','PF偏差(Rc=5R,N=400)','DFEPF偏差(Rc=5R,N=400)');
xlabel('time step');
ylabel('RMS预测偏差');
figure;
hold on;
box on;
p1=plot(1:T,Tekf,'-k.','lineWidth',2);
p2=plot(1:T,Tukf,'-m^','lineWidth',2);
p3=plot(1:T,Tpf,'-ro','lineWidth',2);
p4=plot(1:T,Tepf,'-bp','lineWidth',2);
legend([p1,p2,p3,p4],'EKF时间','UKF时间','PF时间','DFEPF时间');
xlabel('time step');
ylabel('单步时间/s');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 再画一个不同Q、R得到的不同的结果图
% 再画一个偏差曲线图
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- 263
- 264
- 265
- 266
- 267
- 268
- 269
- 270
四、运行结果




五、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]巫茜,罗金彪,顾晓群,曾青.基于改进PSO的无人机三维航迹规划优化算法[J].兵器装备工程学报. 2021,42(08)
[4]邓叶,姜香菊.基于改进人工势场法的四旋翼无人机航迹规划算法[J].传感器与微系统. 2021,40(07)
[5]马云红,张恒,齐乐融,贺建良.基于改进A*算法的三维无人机路径规划[J].电光与控制. 2019,26(10)
[6]焦阳.基于改进蚁群算法的无人机三维路径规划研究[J].舰船电子工程. 2019,39(03)
文章来源: qq912100926.blog.csdn.net,作者:海神之光,版权归原作者所有,如需转载,请联系作者。
原文链接:qq912100926.blog.csdn.net/article/details/119952758
- 点赞
- 收藏
- 关注作者


评论(0)