【基础教程】基于matlab图像去噪总结【含Matlab源码 1274期】

一、获取代码方式

获取代码方式1：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

获取代码方式2：
通过紫极神光博客主页开通CSDN会员，凭支付凭证，私信博主，可获得此代码。

获取代码方式3：
完整代码已上传我的资源：【基础教程】基于matlab图像去噪总结【含Matlab源码 1274期】

备注：开通CSDN会员，仅只能免费获得1份代码（有效期为开通日起，三天内有效）；
订阅紫极神光博客付费专栏，可免费获得2份代码（有效期为订阅日起，三天内有效）；

二、BM3D降噪

BM3D 是一种降噪方法提高了图像在变换域的稀疏表示。BM3D 降噪方法的优点是更好的保留图像中的一些细节，BM3D采用了不同的去噪策略。通过搜索相似块并在变换域进行滤波，得到块评估值，最后对图像中每个点进行加权得到最终去噪效果。 
原理：首先将一幅图像分割成尺寸较小的小像素片，选定参考片后，寻找与参考片相似的小片组成 3D 块。此过程过后将得到 3D 块。然后将所有相似块进行 3D 变换。将变换后的 3D 块进行阈值收缩，这也是除去噪声的过程。然后进行 3D 逆变换。最后将所有的 3D 块通过加权平均后还原到图像中。
BM3D算法的大致流程：
第1步. 初始估计
（1）逐块估计。对含噪图像中的每一块 
（i）分组。找到它的相似块然后把它们聚集到一个三维数组。 
（ii）联合硬阈值。对形成的三维数组进行三维变换，通过对变换域的系数进行硬阈值处理减弱噪声，然后逆变换得到组中所有图像块的估计值，然后把这些估计值返回到他们的原始位置。
（2）聚集。对得到的有重叠的块估计，通过对他们进行加权平均得到真实图像的基础估计。 
第2步. 最终估计 
（1）逐块估计。对基础估计图像中的每一块 
（i） 分组。通过块匹配找到与它相似的相似块在基础估计图像中的位置，通过这些位置得到两个三维数组，一个是从含噪图像中得到的，一个是从基础估计图像中得到的。 
（ii）联合维纳滤波。对形成的两个三维数组均进行三维变换，以基础估计图像中的能量谱作为能量谱对含噪三维数组进行维纳滤波，然后逆变换得到组中所有图像块的估计，然后把这些估计值返回到他们的原始位置。
（2）聚集。对得到的有重叠的局部块估计，通过对他们进行加权平均得到真实图像的最终估计。

三、DCT 降噪

DCT 变换是正交变换。这个方法是对滑动的窗口内的图像做 DCT 变换，在局部变换域做系数收缩。由滑动窗口产的重叠部分满足图像的过完备表示。如果采用的变换不能将普通图像的细节过完备表示，那么这种变换的过完备性就不能抵消无效的收缩。因此只使用二维变换获得稀疏表示只适于特定的图像模式。
B-DCT图像降噪方法一般是处理逐像素滑动的窗口得到的像素矩阵，对矩阵做二维DCT变换，（这以过程可以看作是在矩阵左右两侧同时乘正交矩阵，左乘的矩阵相当于对像素矩阵做列DCT变换，右乘的正交矩阵相当于对像素矩阵做行DCT变换）在变换域中对系数进行硬阈值收缩，然后对收缩后的矩阵做二维DCT逆变换。与B-DCT变换不同的是 SA-DCT变换可以对任意形状的像素片做DCT变换，它的方法是分别对每行和每列做一维DCT变换做完后进行系数收缩，然后再相应一维 DCT 变换的顺序做逆变换。
形状自适应变换域系数收缩降噪方法面临两点问题：1、变换能否适应像素片形状，2、像素片形状是否适应图像的纹理特点。PSA-DCT 方法针对第二点采用 LPA-ICI 方法获得与图像纹理特点对应的像素小片。实验虽然获得了较好的降噪效果，但是 DCT 变换降噪这种方法本质上的问题：1、由于是逐像素滑动变换动窗口带来的数据存储和 DCT 变换计算量较大。2、还有DCT变换基底并没有将自然图像信息与噪声做出良好的分割导致了这类方法的局限性。
一般而言，我们认为图像的噪声在离散余弦变换结果中处在其高频部分，而高频部分的幅值一般很小，利用这一性质，就可以实现去噪。然而，同时会失去图像的部分细节。

%读取图像
X=imread('wangshi.jpg'); 
X=rgb2gray(X);
%读取图像尺寸
[m,n]=size(X); 
%给图像加噪
Xnoised=imnoise(X,'speckle',0.01); 
%输出加噪图像
subplot(121); 
imshow(Xnoised);
%DCT变换
Y=dct2(Xnoised); 
I=zeros(m,n);
%高频屏蔽
I(1:m/3,1:n/3)=1; 
Ydct=Y.*I;
%逆DCT变换
Y=uint8(idct2(Ydct)); 
%结果输出
subplot(122);
imshow(Y);


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
 

四、 PCA 降噪

PCA应用于图像降噪的方法的提出克服了标准正交变换带来的缺点，这种方法对于高结构性的图像细节都有很好的结果。但是由于噪声的存在势必影响主成分分析的准确性。

五、K-SVD 降噪

K-SVD降噪方法解决了固定变换矩阵基底不能自适应图像纹理信息的缺点，，这种算法的缺点是更新字典的计算量较大。

六、非局部均值降噪

早期的降噪方法一般为局部平滑滤波方法，例如，高斯滤波降噪，局部均值滤波降噪。这类方法很难处理图像的非平滑部分，像添加的噪声和图像的纹理信息，去噪的同时不能有效保留纹理信息。非局部均值降噪方法就为解决这一问题。

七、WNNM 降噪

设y=x+n，y是含噪声的图像，x是清晰图像，n是均值为零标准差为σ_n的高斯白噪声。y中局部小片yj，在y寻找yj的相似片，形成矩阵Yj，我们就 Yj=Xj+Nj,Xj和Nj是原图像和噪声形成的矩阵，Xj是一个低阶矩阵，通过这个性质可以解析下式达到降噪的目的：

这是一个WNNM问题，可以通过收缩Yj的奇异值方法解得。首先对Yj做SVD分解，得到特征矩阵U和V还有奇异值矩阵Σ. 对每个奇异值Σij减去权值??，
即Sw (Σ)ij=max(Σ_ii-wi,0)，权值w与Xj的奇异值有关，记Xj的奇异值为：

大的奇异值为Xj的主成分，收缩的少。
小的奇异值收缩的

八、基于主成分分析和双边滤波的图像降噪算法

方法主要分为两步进行处理。第一步首先采用局部像素块匹配算法选出 PCA 的训练样本集，然后应用主成分分析法滤除绝大部分的高斯噪声，第二步对系数收缩重构图像的残余噪声方差进行估计，然后将一步去噪后的图像输入自适应双边滤波器中，最后输出降噪后的图像。

九、小波变换

小波变换作为一种新的时频分析方法，具有多尺度、多分辨率分析的特点，为信号处理提供了一种新的强有力手段。小波变换在图像降噪领域的成功应用主要得益于其具有低熵性、多分辨率特性、去相关性和选基灵活性的优点。
小波降噪本质上是一个信号的滤波问题，实际上是特征提取和低通滤波的综合。波降噪的处理流程是：首先对含有噪声的信号进行多尺度小波变换，在各尺度下尽可能提取出小波系数，最后利用逆小波变换重构信号。
小波去噪是小波变换较为成功的一类应用，其去噪的基本思路为：含噪图像-小波分解-分尺度去噪-小波逆变换-恢复图像。含噪信号经过预处理，然后利用小波变换把信号分解到各尺度中，在每一尺度下把属于噪声的小波系数去掉，保留并增强属于信号的小波系数，最后再经过小波逆变换恢复检测信号。比基于傅里叶变换的去噪方法好。

clear;                 
X=imread('douluodalu.jpg');            
X=rgb2gray(X);
subplot(221);          
imshow(X);             
title('原始图像');                  
% 生成含噪图像并图示
init=2055615866;       
randn('seed',init);      
X=double(X);
% 添加随机噪声
XX=X+8*randn(size(X));  
subplot(222);             
imshow(uint8(XX));              
title(' 含噪图像 ');       
%用小波函数coif2对图像XX进行2层
% 分解
[c,l]=wavedec2(XX,2,'coif2'); 
% 设置尺度向量
n=[1,2];                  
% 设置阈值向量 , 对高频小波系数进行阈值处理
p=[10.28,24.08]; 
nc=wthcoef2('h',c,l,n,p,'s');
% 图像的二维小波重构
X1=waverec2(nc,l,'coif2');   
subplot(223);              
imshow(uint8(X1));                
%colormap(map);            
title(' 第一次消噪后的图像 '); 
%再次对高频小波系数进行阈值处理
mc=wthcoef2('v',nc,l,n,p,'s');
% 图像的二维小波重构
X2=waverec2(mc,l,'coif2');  
subplot(224);             
imshow(uint8(X2));               
title(' 第二次消噪后的图像 ');   


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
 

十、小波阈值降噪

信号通常是低频或者平稳信号的形式，而噪声一般都是高频信号，所以降噪的过程也就是滤除高频信号的一个过程，小波阈值降噪就是利用的这一原理。
小波阈值降噪方法就是通过设置某种阈值，将小波系数与阈值进行比较，将小于阈值的系数设置为 0，而对大于阈值的小波系数，通过某种阈值函数(也称阈值规则)进行修正得到其估计系数。阈值的确定是最为关键的问题。阈值的选择对降噪效果有着很大的影响，如果阈值太小，降噪后的信号仍然有噪声存在，反之，阈值太大则重要的图像特征又将被滤除，造成图像模糊，阈值的选择始终是在抑制噪声和保护图像细节之间折中。目前应用较多的阈值方法包括针对多维正态变量联合分布的 Visushrink 阈值方法、利用均方差准则的无偏估计的 Sureshrink 阈值方法、利用贝叶斯最大后验概率估计理论的 Mapsbrink 阈值方法、利用邻域信息的分块阈值方法等。
1 小波变换的发展
传统的信号理论，是建立在Fourier分析基础上的，而Fourier变换作为一种全局性的变化，有一定的局限性，如不具备局部化分析能力、不能分析非平稳信号等。在实际应用中人们开始对Fourier变换进行各种改进，以改善这种局限性，如STFT（短时傅立叶变换）。由于STFT采用的的滑动窗函数一经选定就固定不变，故决定了其时频分辨率固定不变，不具备自适应能力，而小波分析很好的解决了这个问题。小波变换（wavelet transform，WT）是一种新的变换分析方法，它继承和发展了短时傅立叶变换局部化的思想，同时又克服了窗口大小不随频率变化等缺点，能够提供一个随频率改变的“时间-频率”窗口，是进行信号时频分析和处理的理想工具。它的主要特点是通过变换能够充分突出问题某些方面的特征，解决了Fourier变换的困难问题，成为继Fourier变换以来在科学方法上的重大突破。

2 阈值去噪法的介绍
2.1. 基本原理
小波阈值去噪的基本思想是先设置一个临界阈值λ，若小波系数小于λ，认为该系数主要由噪声引起，去除这部分系数;若小波系数大于λ，则认为此系数主要是由信号引起，保留这部分系数，然后对处理后的小波系数进行小波逆变换得到去噪后的信号。

2.2. 流程图

2.3 阈值函数的选取


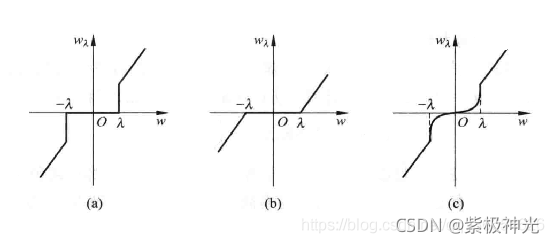
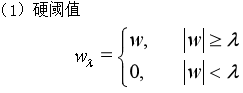
硬阈值是一种简单的置零的方法，而软阈值对于大于阈值的小波系数作了"收缩"，即都减去阈值，从而使输入-输出曲线变成连续的。在阈值选选取上，人们普遍使用软阈值。改进的阈值是硬阈值和软阈值之间的一个折中，即当小波系数小于阈值时，不是简单地置为零，而是平滑地减小为零，当大于阈值时，小波系数幅度都减去阈值。这样，既保证了大的小波系数，又保证了加阈值后系数的平滑过渡。
本次设计自定义了一个折中阈值，当小波系数等于阈值时，在阈值上加了一个折中系数α，实现阈值从硬阈值到软阈值的平缓过渡。折中系数的范围是0-100，即α=0时为硬阈值，α=100时为软阈值，α在0到100的范围之间为折中阈值。

2.4 阈值的选取
小波阈值选取方法有固定阈值（Sqtwolog阈值），风险阈值（Rigrsure阈值），启发式阈值（Heursure阈值），极大极小阈值。这些阈值选取方法中都没有涉及噪声的方差，这与我们的实验理念相违背，在MATLAB中我们对噪声方差进行了单独的处理。取小波系数在各个尺度下绝对值的中值，然后将该中值除以常数0.6745作为该尺度下小波系数中噪声强度的估计，即

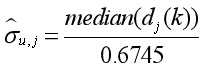
其中，ｊ是小波分解的尺度，dj(k)是小波分解系数，median是MATLAB中求中值运算的命令。则全局阈值为

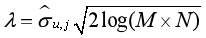
其中M，N是图像的尺度。
2.5 分解函数和重构函数
在MARTLAB中，wavedec2()可以实现图像的多级分解，其格式为

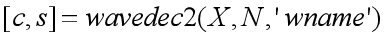
其中c为各层分解系数，s为各层分解系数长度，X为输入图像，N为分解层数，wname为使用的小波基，c的结构为

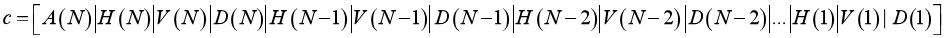
c是一个行向量，其大小为1×size(X)。A(N)代表第N层低频系数,H(N)|V(N)|D(N)代表第N层高频系数,分别是水平,垂直,对角高频。

2.6. 峰值信噪比（PSNR）
峰值信噪比经常用作图像压缩和去噪等领域中信号重建质量的测量方法，它常简单地通过均方差（MSE）进行定义。两个m×n单色图像I和K，如果一个为另外一个的噪声近似，那么它们的的均方差定义为

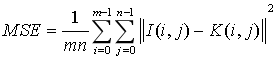
峰值信噪比定义为

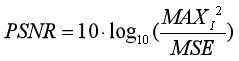
其中MAXI2为单色图像I的尺寸大小
2.7. 实验参数的设计
该设计是在MATLAB2018b环境下编程实现的，经过多次的仿真，我们所选的噪声参数为：均值为0，方差0.02、0.04以及0.06的高斯白噪声。阈值函数用了硬阈值、软阈值和改进的阈值三种方法，阈值选取方式为全局阈值。小波基为db2,它是dbN小波的一种，小波分解级数为3级。所用的图片是自己拍摄的博物馆图片，大小为512x512的灰度图。

3 部分代码
3.1 主函数
代码如下（main.c）

lc,clf,clear

%输入一幅图像
image=imread('Photo.bmp');
%加入不同程度的高斯噪声
image1= imnoise(image, 'gaussian', 0,0.02);
image2= imnoise(image, 'gaussian', 0,0.04);
image3= imnoise(image, 'gaussian', 0,0.06);

figure('NumberTitle', 'off', 'Name', '原图像和噪声图像')
subplot(221);imshow(image);title('原图像');
subplot(222);imshow(image1);title('均值为0，方差为0.02的噪声图像');
subplot(223);imshow(image2);title('均值为0，方差为0.04的噪声图像');
subplot(224);imshow(image3);title('均值为0，方差为0.06的噪声图像');

disp('0.02噪声图像的峰值信噪比：'),psnr(image,image1)
disp('0.04噪声图像的峰值信噪比：'),psnr(image,image2)
disp('0.06噪声图像的峰值信噪比：'),psnr(image,image3)

test_num=randi([1,99],1,1);%随机生成一个数作为折中系数
wname='db2';n=3;input=image1;

subplot(221);
[img1,psn1]=WaveletDenoising(input,n,wname,image,0);
imshow(img1,[]);title('硬阈值去噪后的图像'),
disp('硬阈值去噪后的峰值去噪比：'),psn1
subplot(222);
[img2,psn2]=WaveletDenoising(input,n,wname,image,100);
imshow(img2,[]);title('软阈值去噪后的图像'),
disp('软阈值去噪后的峰值去噪比：'),psn2
subplot(223);
[img3,psn3]=WaveletDenoising(input,n,wname,image,test_num);
imshow(img3,[]);title('随机折中系数去噪后的图像'),
disp('随机折中系数去噪后的峰值去噪比：'),psn3
subplot(224);
[img4,psn4]=WaveletDenoising(input,n,wname,image,-1);
imshow(img4,[]);title('最佳折中系数去噪后的图像'),
disp('最佳折中系数去噪后的峰值去噪比：'),psn4


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
 

3.2 阈值去噪函数
代码如下（WaveletDenoising.m）

function [Image,Psnr]=WaveletDenoising(x,n,wname,image,a)
%函数功能：
%     y=WaveletDenoising(x,n,wname)
%     选择一副图像，加上不同程度的高斯噪声，对带噪图像进行小波分解，
%     对小波系数进行阈值处理再利用处理后的结果重构原图像
%输入参数：
%     x----输入的噪声图像
%     n----小波分解的层数
%     wname----小波基函数
%     a----折中系数
%输出参数：
%     Image----原图像去噪后重构的图像
%    Sndz----峰值信噪比

[c,s]=wavedec2(x,n,wname);                 %进行3层小波分解

for i=1:3  %获取各层各高频分量在c向量中的坐标
    if i==1
        num(i,1)=s(i,1)*s(i,2)+1;                   
        num(i,2)=num(i,1)+s(i+1,1)*s(i+1,2);
        num(i,3)=num(i,2)+s(i+1,1)*s(i+1,2);
        step(i)=s(i+1,1)*s(i+1,2);
    else
        num(i,1)=num(i-1,3)+s(i,1)*s(i,2);
        num(i,2)=num(i,1)+s(i+1,1)*s(i+1,2);
        num(i,3)=num(i,2)+s(i+1,1)*s(i+1,2);
        step(i)=s(i+1,1)*s(i+1,2);
    end
end
C=c;
for j=1:101
    b(j)=0.01*(j-1);                        %折中系数取0到1中的两位小数进行比较
    for i=1:3
        [H,V,D]=detcoef2('a',c,s,i);        %提取第i层各高频系数
        B=[H V D];
        [M,N]=size(B);
        for k=1:M
             for w=1:N
                sigma=median(abs(B(k,w)))/0.6745;%噪声方差
             end
        end
        th=sigma*sqrt(2*log10(M*N));
        
        ch=c(1,num(4-i,1):num(4-i,2)+step(4-i)-1);%对各高频系数进行阈值处理
        C(1,num(4-i,1):num(4-i,2)+step(4-i)-1)=ThresholdProcessing(ch,th,b(j));%阈值处理函数
        cv=c(1,num(4-i,2):num(4-i,2)+step(4-i)-1);
        C(1,num(4-i,2):num(4-i,2)+step(4-i)-1)=ThresholdProcessing(cv,th,b(j));
        cd=c(1,num(4-i,3):num(4-i,2)+step(4-i)-1);
        C(1,num(4-i,3):num(4-i,2)+step(4-i)-1)=ThresholdProcessing(cd,th,b(j));
    end
    ReImage(:,:,j)=waverec2(C,s,wname);%重构图像
    [a1,b1]=size(image);%计算峰值信噪比
    sqr=double(image) - double(ReImage(:,:,j));
    mse= sum(sum( sqr.^2 ))/(a1*b1);
    PSNR(j)= 10*log10( 255*255 / mse ); 
    
end
%返回输出值
a=a+1;
[Ma,Mn]=max(PSNR); 
if a==0
    Psnr=Ma;
    Image=ReImage(:,:,b(Mn)*100);
else
    Image=ReImage(:,:,a);
Psnr=PSNR(a);
end
end


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
 

3.3 阈值处理函数
代码如下（ThresholdProcessing.m）

function y = ThresholdProcessing(A,t,a )
%阈值处理函数
% A为待处理量,t为阈值，a为折中系数

tmp=abs(A)-a*t;
tnp=abs(A)>=t;
y=(sign(A).*tmp).*tnp;

end


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
 

3.4 峰值信噪比
代码如下（psnr.m）

function PSNR = psnr(image1,image2 )
% 计算峰值信噪比
% image1是原图像
% image2是去噪后的图像

[a,b]=size(image1);
sqr=double(image1) - double(image2);
mse= sum(sum( sqr.^2 ))/(a*b);
PSNR= 10*log10( 255*255 / mse );

end


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
 

3.5 折中系数函数
代码如下（main_test.c）

clc,clf,clear

%输入一幅图像
image=imread('Miss.bmp');
% image=rgb2gray(image);
%加入不同程度的高斯噪声
image1= imnoise(image, 'gaussian', 0,0.01);
image2= imnoise(image, 'gaussian', 0,0.02);
image3= imnoise(image, 'gaussian', 0,0.04);

figure(1)
psdn=[]
x=0:100;

for i=0:100
    if i==0
        [img,psn]=WaveletDenoising(image1,3,'db2',image,0);
        psdn=[psdn,psn];
    elseif(i==100)
        [img,psn]=WaveletDenoising(image1,3,'db2',image,100);
        psdn=[psdn,psn];
    else
        [img,psn]=WaveletDenoising(image1,3,'db2',image,i);
        psdn=[psdn,psn];
    end
   plot(psdn);
   disp('迭代次数：'),i
end
xlabel('迭代次数');ylabel('峰值信噪比PSNR');
title('噪声方差0.02，PSNR随折中系数的变化');


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
 

十一、Contourlet 变换

Contourlet 变换是一种多分辨率、多方向的图像稀疏表示方法。它能够用少量的系数有效地表示图像中的轮廓等重要特征。它主要利用了拉普拉斯塔形分解和方向滤波器组来实现图像的稀疏表示。
①改进阈值法：改进阈值法主要有两种改进方法，第一种就是对阈值的选取进行改进，改进后仍然是一个硬阈值，这种方法与全局阈值法有所不同，它是根据系数及其领域系数的关系来计算出阈值，这种方法在一定程度上改善了降噪效果，但是该方法的阈值选取具有一定的随机性，降噪效果不稳定。第二种就是自适应的阈值方法，如引入高频能量比来不断更新阈值，但是这种改进的阈值方法也有一定的缺陷，因为它只是在全局阈值的基础上加了一个调节因子，得到的阈值时不够准确的，降噪效果不是很理想，也会损失图像的细节信息。
②Wiener 滤波：在 Contourlet 分解的基础上加入了 Wiener 滤波这一步骤，它的原理是对 Contourlet 分解的高频系数进行椭圆窗口的 Wiener 滤波；利用自适应窗口的 Wiener 滤波对 Contourlet 分解得到的高频子带进行滤波。
③建模法：据高频系数及其邻域系数的相关性，对这些系数进行 HMT 建模，然后应用到图像中对图像进行降噪处理；对信号方差进行最优估计，然后对图像进行阈值去噪。此类方法的优点是利用了系数间的相关性，缺点是并没有充分利用系数间的相关性。
④改进 Contourlet 降噪算法由于 Contourlet 变换的下采样操作导致 Contourlet没有平移不变性，LP 滤波器组缺乏局部化能力，这使 DFB 频谱中出现了频谱混叠。抗混叠 Contourlet 变换对 LP 的滤波器组进行了一些改进，采用可分离低通滤波器以及满足 Nyquist 抽样定律的高通滤波器来代替 Contourlet 中的 LP 滤波器组，图像通过高通滤波器后级联 DFB，这样使各方向的子带中无法出现由多尺度分解造成的频谱混叠，抑制了频谱混叠问题。

十二、基于平移不变 Contourlet 变换的 SAR 图像降噪

Contourlet 变换会在重构图像中会出现严重的划痕原因是Contourlet 变换在 LP 和 DFB 分解中采用了下采样操作，导致了局部性不够理想，不能够平移不变 。 鉴于这个原因，本文采用了 Eslami 提出的平移不变 Contourlet变换（TICT)，该变换克服了 Contourlet 不能够平移不变的缺点，不仅能很好的抑制噪声，还能达到更强的鲁棒性。

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/119957774