【雷达通信】基于matlab联邦滤波算法惯性+GPS+地磁组合导航仿真【含Matlab源码 1276期】

一、联邦滤波算法简介

面对未来大规模无人机集群任务，若采用集中式的信息融合，计算和通信负担重，并且容错性差。而联邦滤波算法作为一种新型的分散化滤波方法，降低了算法的复杂性，提高了算法的容错性与可靠性，而且联邦滤波算法易于实现，信息分配方式灵活，计算量小。
联邦滤波器中，主滤波器与各子滤波器的状态方程相同，如式所示。假设对式进行n次独立的测量，相应的量测方程如式所示。设Xˆg(k|k)和Pg(k|k)为联邦滤波器的最优估计和协方差阵，Xˆi(k|k)和Pi(k|k)为第i个子滤波器的估计值与协方差阵(i=1,2,⋯,n)，Xˆm(k|k)和Pm(k|k)为主滤波器的估计值和协方差阵。联邦滤波器的一般结构如图所示。

图 联邦滤波结构框架
联邦滤波器的工作流程分为4个步骤。
步骤1信息分配。系统的信息Q−1(k)和P−1g(k|k)在子滤波器与主滤波器的信息分配原则为

步骤2时间更新。子滤波器与主滤波器的时间更新相互独立，其中i=1,2,⋯,n,m，则时间更新方程为

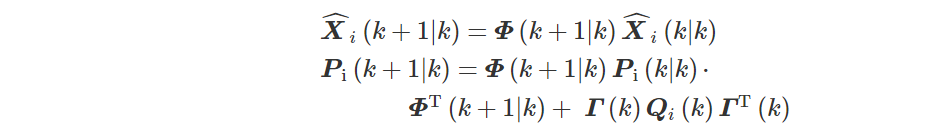
步骤3量测更新。量测更新只在子滤波器中进行，即i=1,2,⋯,n，则量测更新方程为


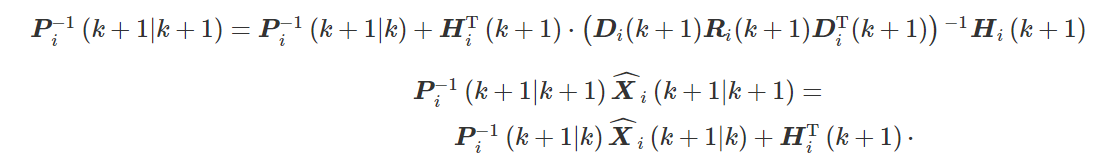
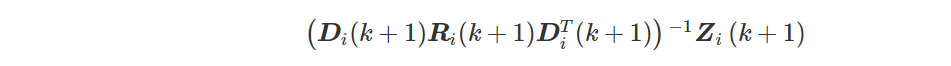
步骤4信息融合。将各个局部滤波器的局部估计值进行融合，得到全局最优估计，即

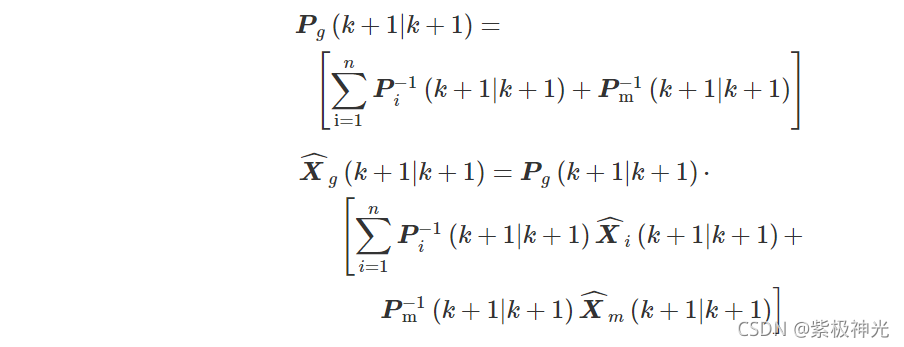
二、部分源代码

% GPS/INS/地磁组合导航，采用联邦滤波算法

clear
R=6378137;
omega=7292115.1467e-11;
g=9.78;
T=14.4;
time=3750;
yinzi1=0.5;
yinzi2=0.5;

%initial value
fai0=30*pi/180;
lamda0=30*pi/180;
vxe0=0.01;
vye0=0.01;

faie0=2.0/60*pi/180;
lamdae0=2.0/60*pi/180;
afae0=3.0/60*pi/180;
beitae0=3.0/60*pi/180;
gamae0=5.0/60*pi/180;

hxjz=pi/4;
vx=20*1852/3600*sin(hxjz);
vy=20*1852/3600*cos(hxjz);
%
weichagps=25;%GPS位置误差
suchagps=0.05;%GPS速度误差
gyroe0=(0.01/3600)*pi/180;
gyrotime=1/7200;%陀螺漂移反向相关时间
atime=1/1800;
gyronoise=(0.001/3600)/180*pi;%陀螺漂移白噪声
beta_d=1/6000.0;     %速度偏移误差反向相关时间
beta_drta=1/6000.0;  %偏流角误差反向相关时间

%matrix of system equation

fai=fai0;
lamada=lamda0;

zong=0*pi/180;
heng=0*pi/180;
hang=45*pi/180;


F(16,16)=0;
G(16,9)=0;




%initial value
x1(16,1)=0;

%the error of sins

xx=x1;

xx(1)=faie0;  %ljn
xx(2)=lamdae0;

xx(5)=afae0;
xx(6)=beitae0;
xx(7)=gamae0;
xx(8)=(0.01/3600)*pi/180;
xx(9)=(0.01/3600)*pi/180;
xx(10)=(0.01/3600)*pi/180;
xx(11)=0.0005;
xx(12)=0.0005;
xx(13)=0.0005;


%w=[gyronoise,gyronoise,gyronoise,gyronoise,gyronoise,gyronoise,g*1e-5,g*1e-5]';
g1=randn(1,time);
g2=randn(1,time);
g3=randn(1,time);
g4=randn(1,time);
g5=randn(1,time);
g6=randn(1,time);
g7=randn(1,time);
g8=randn(1,time);
g9=randn(1,time);


% attitude change matrix

cbn(1,1)=cos(zong)*cos(hang)+sin(zong)*sin(heng)*sin(hang);
cbn(1,2)=-cos(zong)*sin(hang)+sin(zong)*sin(heng)*cos(hang);
cbn(1,3)=-sin(zong)*cos(heng);
cbn(2,1)= cos(heng)*sin(hang);
cbn(2,2)=cos(heng)*cos(hang);
cbn(2,3)=sin(heng);
cbn(3,1)= sin(zong)*cos(hang)-cos(zong)*sin(heng)*sin(hang);
cbn(3,2)=-sin(zong)*sin(hang)-cos(zong)*sin(heng)*cos(hang);
cbn(3,3)=cos(zong)*cos(heng);

F(1,4)=1/R;
F(2,3)=1/(R*cos(fai));
%F(3,1)=2*omega*vx*cos(fai)+vx*vy*sec(fai)^2/R;
F(3,1)=2*omega*vy*cos(fai)+vx*vy*sec(fai)^2/R;
%F(3,3)=vx*tan(fai)/R;
F(3,3)=vy*tan(fai)/R;
F(3,4)=vx*tan(fai)/R+2*omega*sin(fai);
F(3,6)=-g;
%F(4,1)=-(2*omega*vx*cos(fai)+vx^2*sec(fai)^2/R);
F(4,1)=-(2*omega*vx*sin(fai)+vx^2*sec(fai)^2/R);
F(4,3)=-2*(vx*tan(fai)/R+omega*sin(fai));
F(4,5)=g;
%F(4,7)=-g;
F(5,4)=-1/R;
F(5,6)=omega*sin(fai)+vx*tan(fai)/R;
F(5,7)=-(omega*cos(fai)+vx/R);
F(5,8)=1;
F(6,1)=-omega*sin(fai);
%F(6,3)=-1/R;
F(6,3)=1/R;
F(6,5)=-(omega*sin(fai)+vx*tan(fai)/R);
%F(6,7)=-vx/R;
F(6,7)=-vy/R;
F(6,9)=1;
F(7,1)=omega*cos(fai)+vx*sec(fai)^2/R;
F(7,3)=tan(fai)/R;
F(7,5)=omega*cos(fai)+vx/R;
%F(7,6)=vx/R;
F(7,6)=vy/R;
F(7,10)=1;
F(8,8)=-gyrotime;
F(9,9)=-gyrotime;
F(10,10)=-gyrotime;

F(3,11)=cbn(1,1);
F(3,12)=cbn(1,2);
F(3,13)=cbn(1,3);

F(4,11)=cbn(2,1);
F(4,12)=cbn(2,2);
F(4,13)=cbn(2,3);

F(5,8)=cbn(1,1);
F(5,9)=cbn(1,2);
F(5,10)=cbn(1,3);

F(6,8)=cbn(2,1);
F(6,9)=cbn(2,2);
F(6,10)=cbn(2,3);

F(7,8)=cbn(3,1);
F(7,9)=cbn(3,2);
F(7,10)=cbn(3,3);

F(11,11)=-atime;
F
F(16,16)=0;


G=[0,0,0,0,0,0,0,0,0;
    0,0,0,0,0,0,0,0,0;
    0,0,0,0,0,0,0,0,0;
    0,0,0,0,0,0,0,0,0;
    0,0,0,0,0,0,0,0,0;
    0,0,0,0,0,0,0,0,0;
    0,0,0,0,0,0,0,0,0;
    1,0,0,0,0,0,0,0,0;
    0,1,0,0,0,0,0,0,0;
    0,0,1,0,0,0,0,0,0;
    0,0,0,1,0,0,0,0,0;
    0,0,0,0,1,0,0,0,0;
    0,0,0,0,0,1,0,0,0;
    0,0,0,0,0,0,1,0,0;
    0,0,0,0,0,0,0,1,0;
    0,0,0,0,0,0,0,0,1];

[A,B]=c2d(F,G,T);

for i=1:time
    w(1,1)=gyronoise*g1(1,i);
    w(2,1)=gyronoise*g2(1,i);
    w(3,1)=gyronoise*g3(1,i);
    w(4,1)=(0.5*g*1e-5)*g4(1,i);
    w(5,1)=(0.5*g*1e-5)*g5(1,i);
    w(6,1)=(0.5*g*1e-5)*g6(1,i);
    w(7,1)=0.005*g7(1,i);
    w(8,1)=1/600*pi/180*g8(1,i);
    w(9,1)=0.0001*g9(1,i);
    xx=A*xx+B*w/T^2;
    
    
    sins1(1,i)=xx(1,1);
    sins1(2,i)=xx(2,1);
    sins1(3,i)=xx(3,1);
    sins1(4,i)=xx(4,1);
    sins1(5,i)=xx(5,1);
    sins1(6,i)=xx(6,1);
    sins1(7,i)=xx(7,1);
    
    s1(i)=xx(1,1)/pi*180*60;




fai0=30*pi/180;
lamda0=30*pi/180;
vxe0=0.01;
vye0=0.01;

faie0=2*pi/(180*60);
lamdae0=2*pi/(180*60);
afae0=3*pi/(180*60);
beitae0=3*pi/(180*60);
gamae0=5*pi/(180*60);

hxjz=pi/4;
vx=20*1842/3600*sin(hxjz);
vy=20*1842/3600*cos(hxjz);
%vx=0;
%vy=0;
fe=0;
fn=0;
fu=g;

% attitude change matrix
zong=0*pi/180;
heng=0*pi/180;
hang=45*pi/180;
cbn(1,1)=cos(zong)*cos(hang)+sin(zong)*sin(heng)*sin(hang);
cbn(1,2)=-cos(zong)*sin(hang)+sin(zong)*sin(heng)*cos(hang);
cbn(1,3)=-sin(zong)*cos(heng);
cbn(2,1)= cos(heng)*sin(hang);
cbn(2,2)=cos(heng)*cos(hang);
cbn(2,3)=sin(heng);
cbn(3,1)= sin(zong)*cos(hang)-cos(zong)*sin(heng)*sin(hang);
cbn(3,2)=-sin(zong)*sin(hang)-cos(zong)*sin(heng)*cos(hang);
cbn(3,3)=cos(zong)*cos(heng);
%
gpstime=1/600;
weichagps=25;%GPS位置误差
suchagps=0.05;%GPS速度误差
gyroe0=(0.01/3600)*pi/180;
gyrotime=1/7200;%陀螺漂移反向相关时间
atime=1/1800;
gyronoise=(0.01/3600)/180*pi;%陀螺漂移白噪声


tcm2time=1/300;
tcm2noise=0.04*pi/(60*180);
afatcm2=6*pi/(180*60);
betatcm2=6*pi/(180*60);
gamatcm2=6*pi/(180*60);

%matrix of system equation

fai=fai0;
lamada=lamda0;
F(22,22)=0;
F(1,4)=1/R;

F(2,1)=vx*tan(fai)*sec(fai)/R;
F(2,3)=sec(fai)/R;

F(3,1)=2*omega*vx*cos(fai)+vx*vy*sec(fai)^2/R;
F(3,3)=vx*tan(fai)/R;
F(3,4)=vx*tan(fai)/R+2*omega*sin(fai);
F(3,6)=-fu;
F(3,7)=fn;

F(4,1)=-(2*omega*vx*cos(fai)+vx^2*sec(fai)^2/R);
F(4,3)=-2*(vx*tan(fai)/R+omega*sin(fai));
F(4,5)=fu;
F(4,7)=-fe;

F(5,4)=-1/R;
F(5,6)=omega*sin(fai)+vx*tan(fai)/R;
F(5,7)=-(omega*cos(fai)+vx/R);
%F(5,8)=1;
F(6,1)=-omega*sin(fai);
F(6,3)=1/R;
F(6,5)=-(omega*sin(fai)+vx*tan(fai)/R);
F(6,7)=-vx/R;
%F(6,9)=1;
F(7,1)=omega*cos(fai)+vx*sec(fai)^2/R;
F(7,3)=tan(fai)/R;
F(7,5)=omega*cos(fai)+vx/R;
F(7,6)=vx/R;
%F(7,10)=1;
F(5,8)=cbn(1,1);
F(5,9)=cbn(1,2);
F(5,10)=cbn(1,3);
F(5,11)=cbn(1,1);
F(5,12)=cbn(1,2);


Q=[2*gyronoise^2/7200,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
    0,2*gyronoise^2/7200,0,0,0,0,0,0,0,0,0,0,0,0,0;
    0,0,2*gyronoise^2/7200,0,0,0,0,0,0,0,0,0,0,0,0;
    0,0,0,gyronoise^2,0,0,0,0,0,0,0,0,0,0,0;
    0,0,0,0,gyronoise^2,0,0,0,0,0,0,0,0,0,0;
    0,0,0,0,0,gyronoise^2,0,0,0,0,0,0,0,0,0;
    0,0,0,0,0,0,2*5*g*1e-5/1800,0,0,0,0,0,0,0,0;
    0,0,0,0,0,0,0,2*5*g*1e-5/1800,0,0,0,0,0,0,0;
    0,0,0,0,0,0,0,0,2*(25/R)^2/600,0,0,0,0,0,0;
    0,0,0,0,0,0,0,0,0,2*(25/R)^2/600,0,0,0,0,0;
    0,0,0,0,0,0,0,0,0,0,2*0.05^2/600,0,0,0,0;
    0,0,0,0,0,0,0,0,0,0,0,2*0.05^2/600,0,0,0;
    0,0,0,0,0,0,0,0,0,0,0,0,2*tcm2noise^2/300,0,0;
    0,0,0,0,0,0,0,0,0,0,0,0,0,2*tcm2noise^2/300,0;
    0,0,0,0,0,0,0,0,0,0,0,0,0,0,2*tcm2noise^2/300];
Q1=1/yinzi1*Q;
Q2=1/yinzi2*Q;

r=[(weichagps/R)^2,0,0,0,0,0,0;
    0,(weichagps/R)^2,0,0,0,0,0;
    0 , 0,suchagps^2,0,0,0,0;
    0, 0, 0, suchagps^2,0,0,0;
    0,0,0,0,tcm2noise^2,0,0;
    0,0,0,0,0,tcm2noise^2,0;
    0,0,0,0,0,0,tcm2noise^2];
r1=[(weichagps/R)^2,0,0,0;
    0,(weichagps/R)^2,0,0;
    0 , 0,suchagps^2,0;
    0, 0, 0, suchagps^2];
r2=[tcm2noise^2,0,0;
    0,tcm2noise^2,0;
    0,0,tcm2noise^2];


%discrete manage
[A,B]=c2d(F,G,T);
r1=r1/T;
r2=r2/T;
Q1=Q1/T;
Q2=Q2/T;



%initial value
p=[faie0^2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;


figure(1);
subplot(3,2,1)
plot(t,sg1,'b:')
grid
xlabel('time(h)')
ylabel('纬度误差估计（角分）')
subplot(3,2,2)
plot(t,ss1,'b:')
grid
xlabel('time(h)')
ylabel('误差的残差曲线（角分）')
subplot(3,2,3)
plot(t,sg2 ,'b:')
grid
xlabel('time(h)')
ylabel('经度误差估计（角分）')
subplot(3,2,4)
plot(t,ss2 ,'b:')
grid
xlabel('time(h)')
ylabel('误差的残差曲线（角分）')
set(gcf,'color',[1 1 1])


figure(2);
subplot(3,2,1)
plot(t,sg3,'b:')
grid
xlabel('time(h)')
ylabel('东向速度误差估计（kn）')
subplot(3,2,2)
plot(t,ss3,'b:')
grid
xlabel('time(h)')
ylabel('误差的残差曲线（kn）')

subplot(3,2,3)
plot(t,sg4 ,'b:')
grid
xlabel('time(h)')
ylabel('北向速度误差估计(kn)')
subplot(3,2,4)
plot(t,ss4 ,'b:')
grid
xlabel('time(h)')
ylabel('误差的残差曲线(kn)')
set(gcf,'color',[1 1 1])

figure(3);
subplot(3,2,1)
plot(t,sg5,'b:')
grid
xlabel('time(h)')
ylabel('纵摇角误差估计（角分）')
subplot(3,2,2)
plot(t,ss5,'b:')
grid
xlabel('time(h)')
ylabel('误差的残差曲线（角分）')

subplot(3,2,3)
plot(t,sg6 ,'b:')
grid
xlabel('time(h)')
ylabel('横摇角误差估计（角分）')
subplot(3,2,4)
plot(t,ss6 ,'b:')
grid
xlabel('time(h)')
ylabel('误差的残差曲线（角分）')

subplot(3,2,5)
plot(t,sg7 ,'b:')
grid
xlabel('time(h)')
ylabel('首向角误差估计（角分）')
subplot(3,2,6)
plot(t,ss7 ,'b:')
grid
xlabel('time(h)')
ylabel('误差的残差曲线（角分）')
set(gcf,'color',[1 1 1])


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
  
144
  
145
  
146
  
147
  
148
  
149
  
150
  
151
  
152
  
153
  
154
  
155
  
156
  
157
  
158
  
159
  
160
  
161
  
162
  
163
  
164
  
165
  
166
  
167
  
168
  
169
  
170
  
171
  
172
  
173
  
174
  
175
  
176
  
177
  
178
  
179
  
180
  
181
  
182
  
183
  
184
  
185
  
186
  
187
  
188
  
189
  
190
  
191
  
192
  
193
  
194
  
195
  
196
  
197
  
198
  
199
  
200
  
201
  
202
  
203
  
204
  
205
  
206
  
207
  
208
  
209
  
210
  
211
  
212
  
213
  
214
  
215
  
216
  
217
  
218
  
219
  
220
  
221
  
222
  
223
  
224
  
225
  
226
  
227
  
228
  
229
  
230
  
231
  
232
  
233
  
234
  
235
  
236
  
237
  
238
  
239
  
240
  
241
  
242
  
243
  
244
  
245
  
246
  
247
  
248
  
249
  
250
  
251
  
252
  
253
  
254
  
255
  
256
  
257
  
258
  
259
  
260
  
261
  
262
  
263
  
264
  
265
  
266
  
267
  
268
  
269
  
270
  
271
  
272
  
273
  
274
  
275
  
276
  
277
  
278
  
279
  
280
  
281
  
282
  
283
  
284
  
285
  
286
  
287
  
288
  
289
  
290
  
291
  
292
  
293
  
294
  
295
  
296
  
297
  
298
  
299
  
300
  
301
  
302
  
303
  
304
  
305
  
306
  
307
  
308
  
309
  
310
  
311
  
312
  
313
  
314
  
315
  
316
  
317
  
318
  
319
  
320
  
321
  
322
  
323
  
324
  
325
  
326
  
327
  
328
  
329
  
330
  
331
  
332
  
333
  
334
  
335
  
336
  
337
  
338
  
339
  
340
  
341
  
342
  
343
  
344
  
345
  
346
  
347
  
348
  
349
  
350
  
351
  
352
  
353
  
354
  
355
  
356
  
357
  
358
  
359
  
360
  
361
  
362
  
363
  
364
  
365
  
366
  
367
  
368
  
369
  
370
  
371
  
372
  
373
  
374
  
375
  
376
  
377
  
378
  
379
  
380
  
381
  
382
  
383
  
384
  
385
  
386
  
387
  
388
  
389
  
390
  
391
  
392
  
393
  
394
  
395
  
396
  
397
  
398
  
399
  
400
  
401
  
402
  
403
  
404
  
405
  
406
  
407
  
408
  
409
  
410
  
411
  
412
  
413
  
414
  
415
  
416
  
417
  
418
  
419
  
420
  
421
  
422
 

三、运行结果

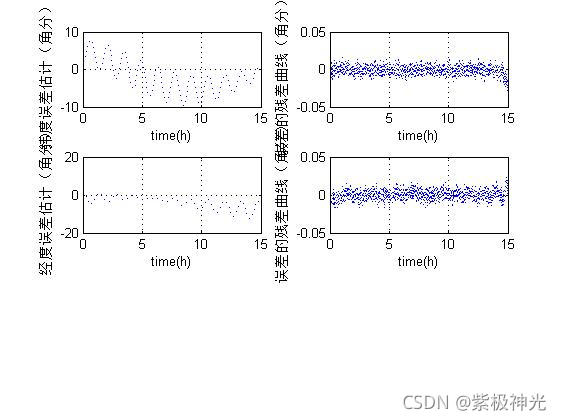
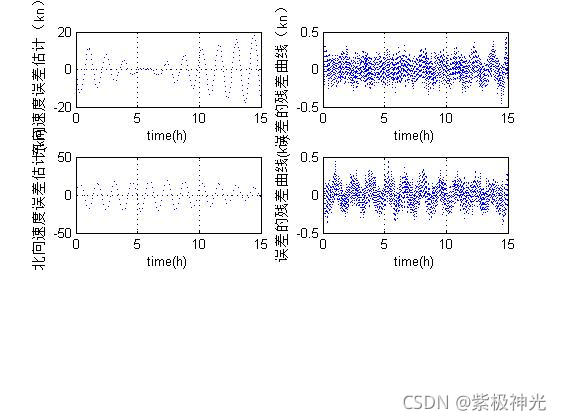
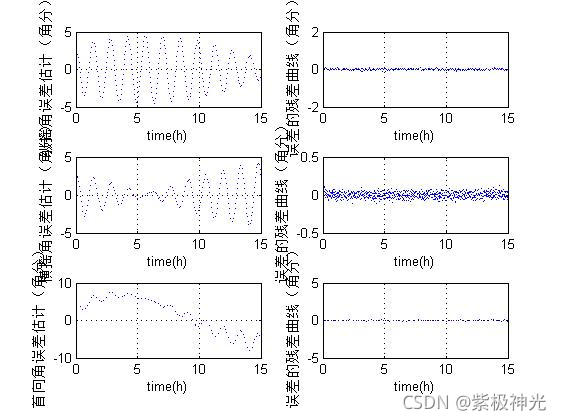
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 沈再阳.精通MATLAB信号处理[M].清华大学出版社，2015.
[2]高宝建,彭进业,王琳,潘建寿.信号与系统——使用MATLAB分析与实现[M].清华大学出版社，2020.
[3]王文光,魏少明,任欣.信号处理与系统分析的MATLAB实现[M].电子工业出版社，2018.
[4]李树锋.基于完全互补序列的MIMO雷达与5G MIMO通信[M].清华大学出版社.2021
[5]何友,关键.雷达目标检测与恒虚警处理（第二版）[M].清华大学出版社.2011

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/120063881