【优化算法】人工生态系统优化算法（AEO）【含Matlab源码 023期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【优化算法】人工生态系统优化算法（AEO）【含Matlab源码 023期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、人工生态系统算法简介

基于人工生态系统的优化（AEO）是一种解决优化问题的新型优化方法。 SDO受地球生态系统中能量流的驱动，该算法模仿了生物的三种独特行为，包括生产，消耗和分解。
AEO算法是Zhao等[27]于2019年通过模拟地球生态系统中能量流动而提出一种新型元启发式优化算法,该算法通过生产算子、消费算子和分解算子对生态系统中的生产、消费和分解行为进行模拟来达到求解优化问题的目的。生产算子旨在加强AEO算法勘探和开发之间的平衡能力;消费算子用于改进AEO算法的探索能力;分解算子旨在提升AEO算法的开发性能。与传统群智能算法相比,AEO算法不但实现简单,除群体规模和最大迭代次数外,无需调整其他任何参数,且具有较好的寻优精度和全局搜索能力。

1 AEO算法遵行以下3个准则
①生态系统作为种群包括3种生物:生产者、消费者和分解者,且种群中分别只有一个个体作为生产者和分解者,其他个体作为消费者;
②每个个体都具有相同的概率被选择为食肉动物、食草动物或杂食动物;
③群体中每个个体的能量水平通过适应度值进行评价,适应度值按降序排序,适应度值越大表示最小化问题的能量水平越高。

2 AEO算法数学描述
**a. 生产者。**生态系统中,生产者可以利用CO2、水和阳光以及分解者提供的营养来产生食物能量。在AEO算法中,种群中的生产者(最差个体)通过搜索空间上下限和分解者(最优个体)进行更新,更新后的个体将引导种群中的其他个体搜索不同的区域。
模拟生产者行为的数学模型如下:

式中:x1为生产者个体空间位置;xn为当前群体中最佳个体空间位置;n为种群规模;T为最大迭代次数;t为当前迭代次数;xrand为搜索空间中随机生成的个体空间位置;U、L分别为空间上、下限;r、r1为[0,1]之间的随机数。

**b. 消费者。**生产者提供食物能量后,每个消费者均可随机选择能量水平较低的消费者或生产者或两者兼有获得食物能量。如果消费者被随机选择为食草动物,它只以生产者为食;如果消费者被随机选择为食肉动物,它只能随机选择能量水平较高的消费者为食;如果消费者被随机选择为杂食动物,它可以同时选择能量水平较高的消费者和生产者为食。模拟食草动物、食肉动物、杂食动物消费行为的数学模型分别为

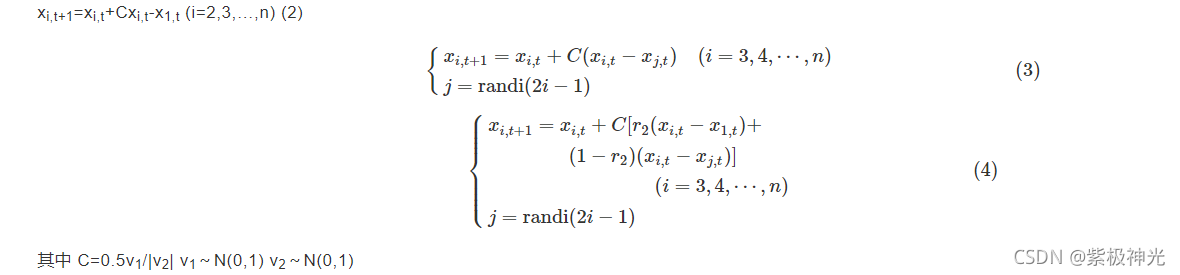
式中:xi为第i个消费者个体空间位置;C为具有levy飞行特性的消费因子;N(0,1)为呈正态分布、均值为0、标准差为1的概率密度函数;xj为具有较高能量水平的消费者和生产者;r2为[0,1]范围内的随机数。

**c. 分解者。**就生态系统功能而言,分解是一个非常重要的过程,它为生产者提供必要的养分。为提高算法的开发性能,AEO算法允许每个个体的下一个位置围绕最佳个体(分解者)传播,并通过调节分解因子D和权重系数e、h来更新群体中第i个消费者的空间位置。其模拟分解行为的数学模型为

2 组合生长模型
a. Weibull模型。Weibull模型最早由瑞典工程师Waloddi Weibull于1951年提出并逐渐发展而来,目前已在油气田产量、地基沉降、泥石流预警、药物溶出曲线评价等领域得到应用。Weibull模型表述形式多样,本文利用式(6)所示函数模型进行需水预测。

式中:W′1为Weibull模型需水预测值;zˆ′o为第b个需水预测影响因子归一化值,即第o维输入向量;α、γ、βo(o=1,2,…,m,本文需水预测影响因子有7个,m=7)为待优化参数。

b. Richards模型。Richards模型是描述生物生长的非线性回归方程,含有4个参数,目前已在碳排放量预测、人口预测、地表沉降等领域得到应用。Richards模型表述形式多样,本文利用式(7)所示函数模型进行需水预测。

式中:W′2为Richards模型需水预测值;a、b、co、d为待优化参数。

c. Usher模型。Usher模型最早由美国学者Usher于1980年提出用于描述增长信息随时间变化的数学模型,目前已在围岩变形预测、油田开发、沉降预测等领域得到应用。Usher模型表述形式多样,本文利用式(8)所示函数模型进行需水预测。

式中:W′3为Usher模型需水预测值;A、B、Co、D为待优化参数。
利用AEO算法对Weibull-Richards-Usher、Weibull-Richards、Weibull-Usher、Richards-Usher模型参数和权重系数进行优化,得到待优化的4种组合生长模型:

三、部分源代码

%--------------------------------------------------------------------------

% --------------------------------------------------------------------------

clc;
clear;
 
MaxIteration=500; 
PopSize=50;
FunIndex=1;
[BestX,BestF,HisBestF]=AEO(FunIndex,MaxIteration,PopSize);


display(['F_index=', num2str(FunIndex)]);
display(['The best fitness is: ', num2str(BestF)]);
%display(['The best solution is: ', num2str(BestX)]);
 if BestF>0
     semilogy(HisBestF,'r','LineWidth',2);
 else
     plot(HisBestF,'r','LineWidth',2);
 end
 xlabel('Iterations');
 ylabel('Fitness');
 title(['F',num2str(FunIndex)]);
%--------------------------------------------------------------------------

% --------------------------------------------------------------------------

% Artificial ecosystem-based optimization (AEO)

function [BestX,BestF,HisBestFit]=AEO(F_index,MaxIt,nPop)


% FunIndex: Index of function.
% MaxIt: The maximum number of iterations.
% PopSize: The size of population.
% PopPos: The position of population.
% PopFit: The fitness of population.
% Dim: The dimensionality of prloblem.
% C: The consumption factor.
% D: The decomposition factor.
% BestX: The best solution found so far. 
% BestF: The best fitness corresponding to BestX. 
% HisBestFit: History best fitness over iterations. 
% Low: The low bound of search space.
% Up: The up bound of search space.


[Low,Up,Dim]=FunRange(F_index); 

for i=1:nPop   
        PopPos(i,:)=rand(1,Dim).*(Up-Low)+Low;
        PopFit(i)=BenFunctions(PopPos(i,:),F_index,Dim);   
end
BestF=inf;
BestX=[];

[NFit, indF]=sort(PopFit,'descend');

PopPos=PopPos(indF,:);
PopFit=PopFit(indF);

BestF=PopFit(end);
BestX=PopPos(end,:);

HisBestFit=zeros(MaxIt,1);
Matr=[1,Dim];

for It=1:MaxIt    
    r1=rand;
    a=(1-It/MaxIt)*r1;
    xrand=rand(1,Dim).*(Up-Low)+Low;
    newPopPos(1,:)=(1-a)*PopPos(nPop,:)+a*xrand; %equation (1)
         
    u=randn(1,Dim);
    v=randn(1,Dim);  
    C=1/2*u./abs(v); %equation (4)
    newPopPos(2,:)=PopPos(2,:)+C.*(PopPos(2,:)-newPopPos(1,:)); %equation (6)
 
      for i=3:nPop
  
   u=randn(1,Dim);
   v=randn(1,Dim);  
   C=1/2*u./abs(v);  
   r=rand;
  if r<1/3
   newPopPos(i,:)=PopPos(i,:)+C.*(PopPos(i,:)-newPopPos(1,:)); %equation (6)
  else
    if 1/3<r<2/3            
        newPopPos(i,:)=PopPos(i,:)+C.*(PopPos(i,:)- PopPos(randi([2 i-1]),:)); %equation (7)
        
    else    
        r2=rand;  
        newPopPos(i,:)=PopPos(i,:)+C.*(r2.*(PopPos(i,:)- newPopPos(1,:))+(1-r2).*(PopPos(i,:)-PopPos(randi([2 i-1]),:))); %equation (8)
 
    end
end
        
      end       
        
         for i=1:nPop        
             newPopPos(i,:)=SpaceBound(newPopPos(i,:),Up,Low);
             newPopFit(i)=BenFunctions(newPopPos(i,:),F_index,Dim);    
                if newPopFit(i)<PopFit(i)
                   PopFit(i)=newPopFit(i);
                   PopPos(i,:)=newPopPos(i,:);
                end
         end
         
         [BestOne indOne]=min(PopFit);
     for i=1:nPop
            r3=rand;   Ind=round(rand)+1;
    newPopPos(i,:)=PopPos(indOne,:)+3*randn(1,Matr(Ind)).*((r3*randi([1 2])-1)*PopPos(indOne,:)-(2*r3-1)*PopPos(i,:)); %equation (9)
      end
     
      for i=1:nPop        
             newPopPos(i,:)=SpaceBound(newPopPos(i,:),Up,Low);
             newPopFit(i)=BenFunctions(newPopPos(i,:),F_index,Dim);    
                if newPopFit(i)<PopFit(i)
                   PopPos(i,:)=newPopPos(i,:);
                    PopFit(i)=newPopFit(i);
                end
      end
         
      [NFit,indF]=sort(PopFit,'descend');

      PopPos=PopPos(indF,:);
      PopFit=PopFit(indF);
      
      
    for i=1:nPop
        if PopFit(end)<BestF
            BestF=PopFit(end);
            BestX=PopPos(end,:);
            
        end
    end   
    
          
HisBestFit(It)=BestF;
         
end 

function Fit=BenFunctions(X,FunIndex,Dim)




 switch FunIndex
     
   %%%%%%%%%%%%%%%%%%%%%%%%%%unimodal function%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%   
  
%Sphere
case 1
Fit=sum(X.^2);

%Schwefel 2.22
case 2 
Fit=sum(abs(X))+prod(abs(X));

%Schwefel 1.2
case 3
    Fit=0;
    for i=1:Dim
    Fit=Fit+sum(X(1:i))^2;
    end

%Schwefel 2.21
case 4
    Fit=max(abs(X));

%Rosenbrock
case 5
    Fit=sum(100*(X(2:Dim)-(X(1:Dim-1).^2)).^2+(X(1:Dim-1)-1).^2);

%Step
case 6
    Fit=sum(floor((X+.5)).^2);

%Quartic
case 7
    Fit=sum([1:Dim].*(X.^4))+rand;


%%%%%%%%%%%%%%%%%%%%%%%%%%multimodal function%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%Schwefel
case 8
    Fit=sum(-X.*sin(sqrt(abs(X))));

%Rastrigin
case 9
    Fit=sum(X.^2-10*cos(2*pi.*X))+10*Dim;

%Ackley
case 10
    Fit=-20*exp(-.2*sqrt(sum(X.^2)/Dim))-exp(sum(cos(2*pi.*X))/Dim)+20+exp(1);

%Griewank
case 11
    Fit=sum(X.^2)/4000-prod(cos(X./sqrt([1:Dim])))+1;

%Penalized
case 12
  a=10;k=100;m=4;
  Dim=length(X);
  Fit=(pi/Dim)*(10*((sin(pi*(1+(X(1)+1)/4)))^2)+sum((((X(1:Dim-1)+1)./4).^2).*...
        (1+10.*((sin(pi.*(1+(X(2:Dim)+1)./4)))).^2))+((X(Dim)+1)/4)^2)+sum(k.*...
        ((X-a).^m).*(X>a)+k.*((-X-a).^m).*(X<(-a)));

%Penalized2
case 13
  a=10;k=100;m=4;
  Dim=length(X);
  Fit=.1*((sin(3*pi*X(1)))^2+sum((X(1:Dim-1)-1).^2.*(1+(sin(3.*pi.*X(2:Dim))).^2))+...
        ((X(Dim)-1)^2)*(1+(sin(2*pi*X(Dim)))^2))+sum(k.*...
        ((X-a).^m).*(X>a)+k.*((-X-a).^m).*(X<(-a)));

%%%%%%%%%%%%%%%%%%%%%%%%%%fixed-dimensionalmultimodalfunction%%%%%%%%%%%%%%

%Foxholes
case 14
  a=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...
  -32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];
    for j=1:25
        b(j)=sum((X'-a(:,j)).^6);
    end
    Fit=(1/500+sum(1./([1:25]+b))).^(-1);

%Kowalik
case 15
    a=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];
    b=[.25 .5 1 2 4 6 8 10 12 14 16];b=1./b;
    Fit=sum((a-((X(1).*(b.^2+X(2).*b))./(b.^2+X(3).*b+X(4)))).^2);

%Six Hump Camel
case 16
    Fit=4*(X(1)^2)-2.1*(X(1)^4)+(X(1)^6)/3+X(1)*X(2)-4*(X(2)^2)+4*(X(2)^4);

%Branin
case 17
    Fit=(X(2)-(X(1)^2)*5.1/(4*(pi^2))+5/pi*X(1)-6)^2+10*(1-1/(8*pi))*cos(X(1))+10;

%GoldStein-Price
case 18
    Fit=(1+(X(1)+X(2)+1)^2*(19-14*X(1)+3*(X(1)^2)-14*X(2)+6*X(1)*X(2)+3*X(2)^2))*...
        (30+(2*X(1)-3*X(2))^2*(18-32*X(1)+12*(X(1)^2)+48*X(2)-36*X(1)*X(2)+27*(X(2)^2)));

%Hartman 3
case 19
  a=[3 10 30;.1 10 35;3 10 30;.1 10 35];c=[1 1.2 3 3.2];
  p=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];
  Fit=0;
  for i=1:4

  end

end
 


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
  
144
  
145
  
146
  
147
  
148
  
149
  
150
  
151
  
152
  
153
  
154
  
155
  
156
  
157
  
158
  
159
  
160
  
161
  
162
  
163
  
164
  
165
  
166
  
167
  
168
  
169
  
170
  
171
  
172
  
173
  
174
  
175
  
176
  
177
  
178
  
179
  
180
  
181
  
182
  
183
  
184
  
185
  
186
  
187
  
188
  
189
  
190
  
191
  
192
  
193
  
194
  
195
  
196
  
197
  
198
  
199
  
200
  
201
  
202
  
203
  
204
  
205
  
206
  
207
  
208
  
209
  
210
  
211
  
212
  
213
  
214
  
215
  
216
  
217
  
218
  
219
  
220
  
221
  
222
  
223
  
224
  
225
  
226
  
227
  
228
  
229
  
230
  
231
  
232
  
233
  
234
  
235
  
236
  
237
  
238
  
239
  
240
  
241
  
242
  
243
  
244
  
245
  
246
  
247
  
248
  
249
  
250
  
251
  
252
  
253
  
254
  
255
  
256
  
257
  
258
  
259
  
260
 

四、运行结果

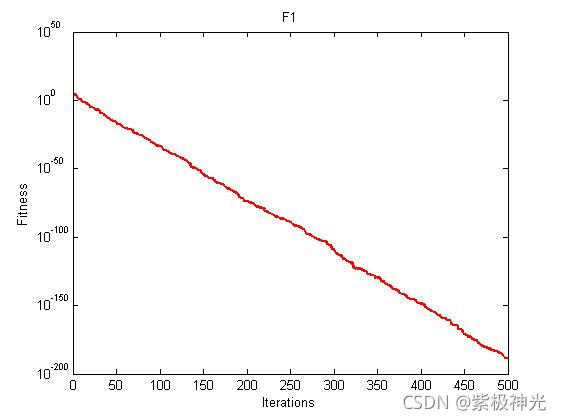
五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/119986250