【飞行器】基于matlab四旋翼飞行器PID控制仿真【含Matlab源码 1277期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【飞行器】基于matlab四旋翼飞行器PID控制仿真【含Matlab源码 1277期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、四旋翼飞行器简介

0 引 言
四旋翼飞行器由于具有可垂直起降、机动性强、操作方便等诸多优点,在军事和民用场合得到广泛应用,从而成为众多学者的研究热点。四旋翼飞行器是具有四输入、六输出的欠驱动、非线性、强耦合系统。其姿态控制精度和抗干扰问题一直是研究重点。目前国内较普遍的飞行器控制算法主要包括:反步法、自适应控制、H控制、滑模控制、自抗扰控制等,对实现四旋翼飞行器的姿态控制具有重要的理论和实践意义。文献提出应用反步算法为飞行器上下、前后、左右、偏航4个子系统配置控制律,实现了四旋翼飞行器对设定轨迹的精确跟踪。该算法在构造Lyapunov函数的过程中,是以其导数小于零为前提,因此应用受到局限。文献针对传统的离散线性滑模应用于四旋翼飞行器控制具有跟踪误差大、响应速度慢、不能有限时间收敛等问题,提出了干扰观测器补偿的自适应离散终端滑模控制,使响应时间更快、跟踪效果更理想、鲁棒性更强。文献利用线性扩张状态观测器对四旋翼飞行器内部不确定干扰和外部干扰进行实时估计,进而采取线性状态反馈控制对扰动的估计值进行在线补偿,以实现四旋翼飞行器的姿态控制。

1 四旋翼飞行器动力学模型的建立
1. 1 四旋翼飞行器受力分析
对于飞行器的每个旋翼,剖面呈非对称,一旦旋翼旋转,由于上表面空气流速比下表面快,故上表面受到的空气压力小于下表面,上下表面受到的压差形成升力,如图1所示。旋翼1、3逆时针旋转,旋翼2、4顺时针旋转。由叶素动量理论可知,每个旋翼产生的升力Fi与电机转速ωi的平方成正比,即Fi=kFω2i(i=1,2,3,4),其中kF为升力系数。

图1 四旋翼飞行器受力分析图
当旋翼旋转时,空气阻力会阻碍其旋转。这种阻力形成施加在机体上的反扭转力矩,当4个旋翼转速相等时,旋翼产生的反扭矩作用相互抵消。四旋翼飞行器通过改变2对正反螺旋桨的转速实现对其运动控制。在4个旋翼转速相等的情况下,同时增加或者减少4个旋翼转速,可以实现飞行器上升或者下降。如果4个旋翼产生的升力之和等于机体重力,可以实现飞行器空中悬停。保持旋翼2、4的转速不变,改变旋翼1或者旋翼3的转速,飞行器在力矩l(F3-F1)或l(F1-F3)的作用下(其中l为电机轴线到飞行器中心距离),可实现俯仰运动。保持旋翼1和旋翼3的转速不变,改变旋翼2或者旋翼4的转速,飞行器在力矩l(F4-F2)或l(F2-F4)的作用下,可实现横滚运动。如果同时改变旋翼1和旋翼3的转速,或者同时改变旋翼2和旋翼4的转速,并保持飞行器总升力与机体重力相等,飞行器会在反扭矩的作用下实现偏航运动。由此可见,实现飞行器垂直运动的升力,以及实现俯仰、横滚、偏航运动的旋转力矩可以表示为

式中: F——飞行器垂直运动的升力;
Mx、My、Mz——四旋翼俯仰、横滚和偏航运动的旋转力矩;
kF——升力系数;
kM——旋转力矩系数。

1. 2 动力学模型建立
为了描述飞行器的姿态和运动状态,需要引入地理坐标系n(X,Y,Z)与载体坐标系b(x,y,z)。地理坐标系又称为东北天坐标系,载体坐标系与飞行器固连,原点为飞行器中心。将地理坐标系与载体坐标系原点重合,并将地理坐标系分别绕X、Y、Z轴旋转3次之后可得到载体坐标系,地理坐标系到载体坐标系的转换矩阵可表示为


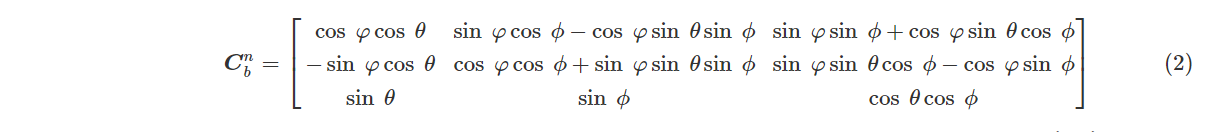
由式(5)和式(2)可求得地理坐标系n中飞行器在X、Y、Z轴方向所受旋翼升力向量:


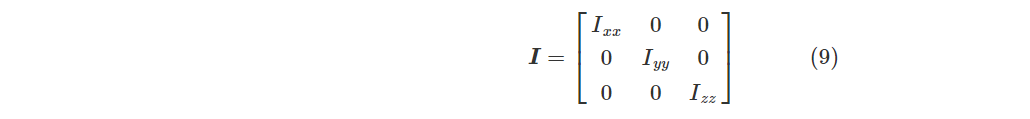
在低速飞行过程中,角速度矢量较小,式(8)中左边第二项可近似认为为零,则式(8)可化简为

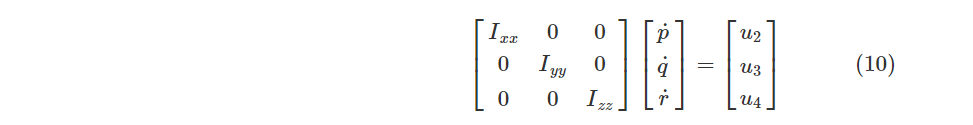
将式(10)转换可得:

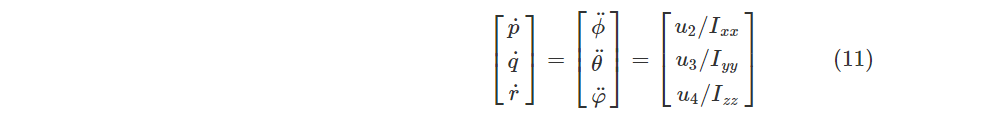
由式(7)和式(11)可得四旋翼飞行器在低速飞行情况下的非线性动力学模型:

由式(12)可知,四旋翼飞行器线运动不影响角运动,但是角运动会影响线运动。以u1、u2、u3、u4为系统输入,通过改变这4个输入变量的值,可以改变飞行器的3个线位移和3个角位移,从而实现对飞行器的运动控制。

2 四旋翼飞行器的控制系统构建与仿真
经典PID算法结构简单,基于偏差设计反馈律,不依赖受控对象的具体数学模型,在很多过程控制中均有良好表现。尽管各种新的控制算法不断涌现,但是并没有改变PID控制算法在工业控制中的主导地位。本文根据四旋翼在飞行过程中经常会遇到不确定外界干扰等情况,设计了基于小扰动的PID控制器,如图2所示。

图2 PID控制器结构图

三、部分源代码及仿真图

clc
clear all
close all

%% 开始仿真
sim('PID_control_for_a_quadrotor');
figure('name','垂直速率随时间变化曲线')
plot(t,dzn,'b:',t,dz,'r-','Linewidth',2);
xlabel('时间(s)');
ylabel('垂直速率(m/s)');
legend('期望','实际');
title('垂直速率随时间变化曲线');
grid on;

figure('name','俯仰角速率随时间变化曲线')
plot(t,dthetan,'b:',t,dtheta,'r-','Linewidth',2);
xlabel('时间(s)');
ylabel('俯仰角速率(rad/s)');
legend('期望','实际');
title('俯仰角速率随时间变化曲线');
grid on;

figure('name','滚转角速率随时间变化曲线')
plot(t,dphin,'b:',t,dphi,'r-','Linewidth',2);
xlabel('时间(s)');
ylabel('滚转角速率(rad/s)');
legend('期望','实际');
title('滚转角速率随时间变化曲线');
grid on;

figure('name','偏航角速率随时间变化曲线')
plot(t,dpsin,'b:',t,dpsi,'r-','Linewidth',2);
xlabel('时间(s)');
ylabel('偏航角速率(rad/s)');
legend('期望','实际');
title('偏航角速率随时间变化曲线');
grid on;



  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
 

四、运行结果

五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]张萍.四旋翼飞行器姿态控制建模与仿真[J].电机与控制应用. 2019,46(12)
[4]刘岩,杨牧.四旋翼飞行器飞行控制系统研究与设计[J].山东工业技术. 2019,(07)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/120064155