【ACO三维路径规划】基于matlab蚁群算法无人机三维路径规划【含Matlab源码 1278期】
一、无人机简介
0 引言
随着现代技术的发展,飞行器种类不断变多,应用也日趋专一化、完善化,如专门用作植保的大疆PS-X625无人机,用作街景拍摄与监控巡察的宝鸡行翼航空科技的X8无人机,以及用作水下救援的白鲨MIX水下无人机等,决定飞行器性能主要是内部的飞控系统和外部的路径规划问题。就路径问题而言,在具体实施任务时仅靠操作员手中的遥控器控制无人飞行器执行相应的工作,可能会对操作员心理以及技术提出极高的要求,为了避免个人操作失误,进而造成飞行器损坏的危险,一种解决问题的方法就是对飞行器进行航迹规划。
飞行器的测量精度,航迹路径的合理规划,飞行器工作时的稳定性、安全性等这些变化对飞行器的综合控制系统要求越来越高。无人机航路规划是为了保证无人机完成特定的飞行任务,并且能够在完成任务的过程中躲避各种障碍、威胁区域而设计出最优航迹路线的问题。
1 常见的航迹规划算法
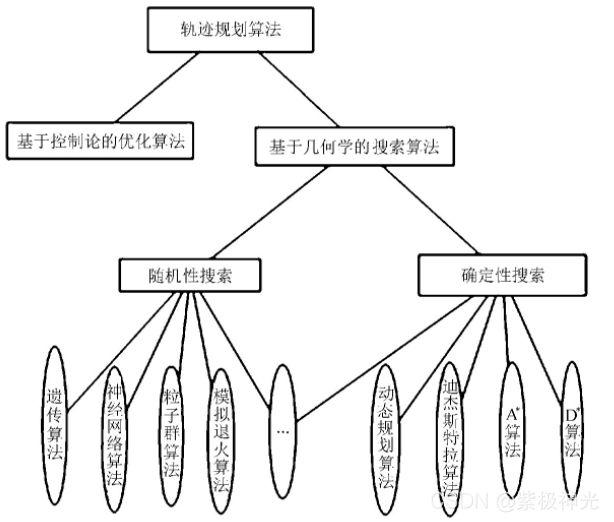
图1 常见路径规划算法
文中主要对无人机巡航阶段的航迹规划进行研究,假设无人机在飞行中维持高度与速度不变,那么航迹规划成为一个二维平面的规划问题。在航迹规划算法中,A算法计算简单,容易实现。在改进A算法基础上,提出一种新的、易于理解的改进A算法的无人机航迹规划方法。传统A算法将规划区域栅格化,节点扩展只限于栅格线的交叉点,在栅格线的交叉点与交叉点之间往往存在一定角度的两个运动方向。将存在角度的两段路径无限放大、细化,然后分别用两段上的相应路径规划点作为切点,找到相对应的组成内切圆的圆心,然后作弧,并求出相对应的两切点之间的弧所对应的圆心角,根据下式计算出弧线的长度
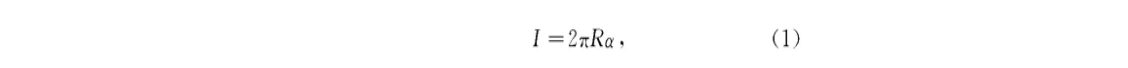
式中:R———内切圆的半径;
α———切点之间弧线对应的圆心角。
二、蚁群算法简介
1 蚁群算法(ant colony algorithm,ACA)起源和发展历程
Marco Dorigo等人在研究新型算法的过程中,发现蚁群在寻找食物时,通过分泌一种称为信息素的生物激素交流觅食信息从而能快速的找到目标,于是在1991年在其博士论文中首次系统地提出一种基于蚂蚁种群的新型智能优化算法“蚂蚁系统(Ant system,简称AS)”,后来,提出者及许多研究者对该算法作了各种改进,将其应用于更为广泛的领域,如图着色问题、二次分配问题、工件排序问题、车辆路径问题、车间作业调度问题、网络路由问题、大规模集成电路设计等。近些年来,M.Dorigo等人把蚂蚁算法进一步发展成一种通用的优化技术“蚁群优化(Ant Colony Optimization,简称ACO)”,并将所有符合ACO框架的算法称为“蚁群优化算法(ACO algorithm)”。
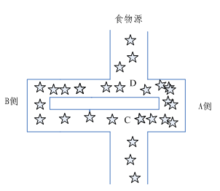
具体来说,各个蚂蚁在没有事先告知食物在什么地方的前提下开始寻找食物。当一只找到食物以后,它会向环境释放一种挥发性分泌物pheromone (称为信息素,该物质随着时间的推移会逐渐挥发消失,信息素浓度的大小表征路径的远近)信息素能够让其他蚂蚁感知从而起到一个引导的作用。通常多个路径上均有信息素时,蚂蚁会优先选择信息素浓度高的路径,从而使浓度高的路径信息素浓度更高,形成一个正反馈。有些蚂蚁并没有像其它蚂蚁一样总重复同样的路,他们会另辟蹊径,如果另开辟的道路比原来的其他道路更短,那么,渐渐地,更多的蚂蚁被吸引到这条较短的路上来。最后,经过一段时间运行,可能会出现一条最短的路径被大多数蚂蚁重复着。最终,信息素浓度最高的路径即是最终被蚂蚁选中的最优路径。
与其他算法相比,蚁群算法是一种比较年轻的算法,具有分布式计算、无中心控制、个体之间异步间接通信等特点,并且易于与其他优化算法相结合,经过不少仁人志士的不断探索,到今天已经发展出了各式各样的改进蚁群算法,不过蚁群算法的原理仍是主干。
2 蚁群算法的求解原理
基于上述对蚁群觅食行为的描述,该算法主要对觅食行为进行以下几个方面模拟:
(1)模拟的图场景中包含了两种信息素,一种表示家,一种表示食物的地点,并且这两种信息素都在以一定的速率进行挥发。
(2)每个蚂蚁只能感知它周围的小部分地方的信息。蚂蚁在寻找食物的时候,如果在感知范围内,就可以直接过去,如果不在感知范围内,就要朝着信息素多的地方走,蚂蚁可以有一个小概率不往信息素多的地方走,而另辟蹊径,这个小概率事件很重要,代表了一种找路的创新,对于找到更优的解很重要。
(3)蚂蚁回窝的规则与找食物的规则相同。
(4)蚂蚁在移动时候首先会根据信息素的指引,如果没有信息素的指引,会按照自己的移动方向惯性走下去,但也有一定的机率改变方向,蚂蚁还可以记住已经走过的路,避免重复走一个地方。
(5)蚂蚁在找到食物时留下的信息素最多,然后距离食物越远的地方留下的信息素越少。找到窝的信息素留下的量的规则跟食物相同。蚁群算法有以下几个特点:正反馈算法、并发性算法、较强的鲁棒性、概率型全局搜索、不依赖严格的数学性质、搜索时间长,易出现停止现象。
蚂蚁转移概率公式:
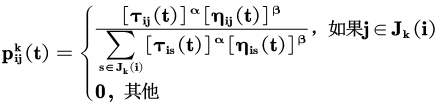
公式中:是蚂蚁k从城市i转移到j的概率;α,β分别为信息素和启发式因子的相对重要程度;为边(i,j)上的信息素量;为启发式因子;为蚂蚁k下步允许选择的城市。上述公式即为蚂蚁系统中的信息素更新公式,是边(i,j)上的信息素量;ρ是信息素蒸发系数,0<ρ<1;为第k只蚂蚁在本次迭代中留在边(i,j)上的信息素量;Q为一正常系数;为第k只蚂蚁在本次周游中的路径长度。
在蚂蚁系统中,信息素更新公式为:
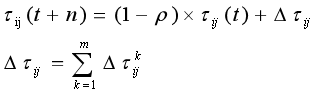
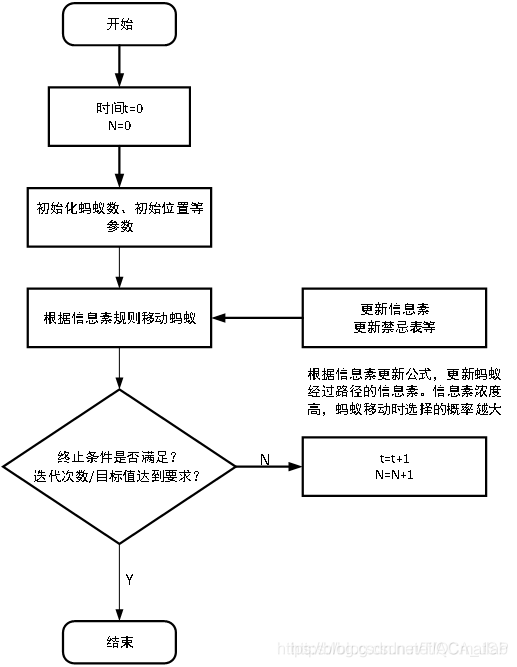
3 蚁群算法的求解步骤:
(1)初始化参数在计算之初,需要对相关参数进行初始化,如蚁群规模(蚂蚁数量)m、信息素重要程度因子α、启发函数重要程度因子β、信息素会发银子ρ、信息素释放总量Q、最大迭代次数iter_max、迭代次数初值iter=1。
(2)构建解空间将各个蚂蚁随机地置于不同的出发点,对每个蚂蚁k(k=1,2,3…m),按照(2-1)计算其下一个待访问城市,直到所有蚂蚁访问完所有城市。
(3)更新信息苏计算每个蚂蚁经过路径长度Lk(k=1,2,…,m),记录当前迭代次数中的最优解(最短路径)。同时,根据式(2-2)和(2-3)对各个城市连接路径上信息素浓度进行更新。
(4) 判断是否终止若iter<iter_max,则令iter=iter+1,清空蚂蚁经过路径的记录表,并返回步骤2;否则,终止计算,输出最优解。
(5)判断是否终止若iter<iter_max,则令iter=iter+1,清空蚂蚁经过路径的记录表,并返回步骤2;否则,终止计算,输出最优解。3. 判断是否终止若iter<iter_max,则令iter=iter+1,清空蚂蚁经过路径的记录表,并返回步骤2;否则,终止计算,输出最优解。
三、部分源代码
%-------------------------------------蚁群算法主函数----------------------------------------------
clc
clear
load data z information
%起点坐标
starty=10;
starth=3;
%终点坐标
endy=8;
endh=5;
n=10;
m=21;
Best=[];
[path,information]=searchpath(n,m,information,z,starty,starth,endy,endh); %路径寻找
fitness=CacuFit(path); %适应度计算
[bestfitness,bestindex]=min(fitness); %最佳适应度
bestpath=path(bestindex,:);
Best=[Best;bestfitness];
% %更新信息素
rou=0.2;
cfit=100/bestfitness;
k=2;
for i=2:m-1
information(k,bestpath(i*2-1),bestpath(i*2))=(1-rou)*information(k,bestpath(i*2-1),bestpath(i*2))+rou*cfit;
end
for kk=1:1:100
kk
[path,information]=searchpath(n,m,information,z,starty,starth,endy,endh); %路径寻找
fitness=CacuFit(path); %适应度计算
[newbestfitness,newbestindex]=min(fitness); %最佳适应度
if newbestfitness<bestfitness
bestfitness=newbestfitness;
bestpath=path(newbestindex,:);
end
Best=[Best;bestfitness];
% %更新信息素
rou=0.2;
cfit=100/bestfitness;
k=2;
for i=2:m-1
information(k,bestpath(i*2-1),bestpath(i*2))=(1-rou)*information(k,bestpath(i*2-1),bestpath(i*2))+rou*cfit;
end
end
for i=1:21
a(i,1)=bestpath(i*2-1);
a(i,2)=bestpath(i*2);
end
k=1:21
figure(1)
x=1:21;
y=1:21;
[x1,y1]=meshgrid(x,y);
%surf(x1,y1,z,'linestyle','none')
mesh(x1,y1,z)
load data z information
axis([1,21,1,21,0,2000])
[x0,y0]=meshgrid(1:0.1:21);
z0=interp2(x,y,z,x0,y0);
mesh(x0,y0,z0)
axis([1,21,1,21,0,2000])
xlabel('km')
ylabel('km')
%寻找路径
%n:路径条数 m分开平面数 information:信息素 z高度表
%starty starth 出发点
%endy endh 终点
%path 寻到路径
function [path,information]=searchpath(n,m,information,z,starty,starth,endy,endh)
ycMax=3; %横向最大变动
hcMax=3; %纵向最大变动
decr=0.9; %衰减概率
for ii=1:n
path(ii,1:2)=[starty,starth];
oldpoint=[starty,starth]; %当前坐标点
for k=2:m-1
%计算所有数据点对应的适应度值
kk=1;
for i=-ycMax:ycMax
for j=-hcMax:hcMax
point(kk,:)=[oldpoint(1)+i,oldpoint(2)+j];
if (point(kk,1)<20)&&(point(kk,1)>0)&&(point(kk,2)<17)&&(point(kk,2)>0)
qfz(kk)=CacuQfz(point(kk,1),point(kk,2),oldpoint(1),oldpoint(2),endy,endh,k,z);
qz(kk)=qfz(kk)*information(k,point(kk,1),point(kk,2));
kk=kk+1;
else
qz(kk)=0;
kk=kk+1;
end
end
end
%选择下个点
sumq=qz./sum(qz);
pick=rand;
while pick==0
pick=rand;
end
for i=1:49
pick=pick-sumq(i);
if pick<=0
index=i;
break;
end
end
oldpoint=point(index,:);
%更新信息素
information(k+1,oldpoint(1),oldpoint(2))=0.5*information(k+1,oldpoint(1),oldpoint(2));
%路径保存
path(ii,k*2-1:k*2)=[oldpoint(1),oldpoint(2)];
end
path(ii,41:42)=[endy,endh];
end
%计算个体适应度值
%path:路径
%fitness:路径适应度值
function fitness=CacuFit(path)
[n,m]=size(path);
for i=1:n
fitness(i)=0;
for j=2:m/2
fitness(i)=fitness(i)+sqrt(1+(path(i,j*2-1)-path(i,(j-1)*2-1))^2+(path(i,j*2)-path(i,(j-1)*2))^2)+abs(path(i,j*2));
end
end
%计算每个点的启发值
%nowy,nowh:现在点
%endy,endh:终点
%oldy,oldh:上个点
%k:当前层数
%z:地形高度图
function qfz=CacuQfz(nowy,nowh,oldy,oldh,endy,endh,k,z)
%点是否可行
if z(nowy,k)<nowh*200
S=1;
else
S=0;
end
ldh*0.2-nowh*0.2)^2+(nowy-oldy)^2)+sqrt((21-k)^2+(endh*0.2-nowh*0.2)^2+(nowy-oldy)^2));
qfz=S*M*D;
%}
kk=1:0.1:21;
xx=interp1(x,k,kk);
yy= interp1(y,a(:,1)',kk);
zz=interp1(x,a(:,2)',kk);
for i=1:length(xx)
plot3(xx(1:i),yy(1:i),zz(1:i)*200,'--or')
pause(0.1);
end
hold off;
figure(2)
plot(Best)
title('最佳个体适应度变化趋势')
xlabel('迭代次数')
ylabel('适应度值')
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
``四、运行结果
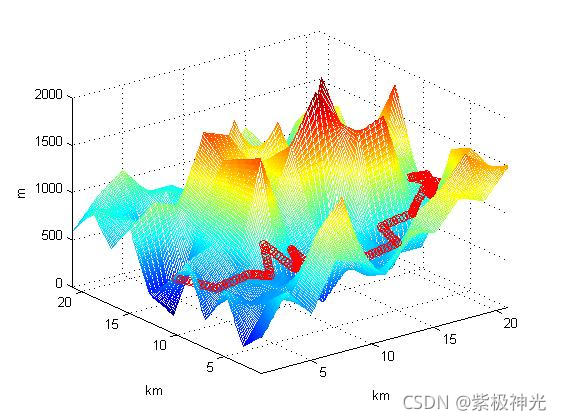
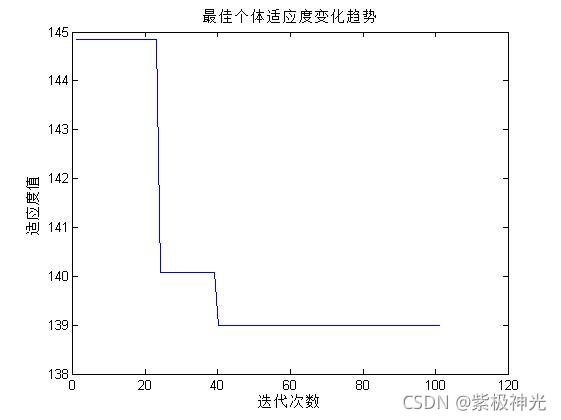
五、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]巫茜,罗金彪,顾晓群,曾青.基于改进PSO的无人机三维航迹规划优化算法[J].兵器装备工程学报. 2021,42(08)
[4]邓叶,姜香菊.基于改进人工势场法的四旋翼无人机航迹规划算法[J].传感器与微系统. 2021,40(07)
[5]马云红,张恒,齐乐融,贺建良.基于改进A*算法的三维无人机路径规划[J].电光与控制. 2019,26(10)
[6]焦阳.基于改进蚁群算法的无人机三维路径规划研究[J].舰船电子工程. 2019,39(03)
文章来源: qq912100926.blog.csdn.net,作者:海神之光,版权归原作者所有,如需转载,请联系作者。
原文链接:qq912100926.blog.csdn.net/article/details/120064469
- 点赞
- 收藏
- 关注作者



评论(0)