【优化覆盖】基于matlab萤火虫算法求解无线网络传感覆盖优化问题【含Matlab源码 1275期】

一、萤火虫优化算法（FA）简介

1 介绍
萤火虫（firefly）种类繁多，主要分布在热带地区。大多数萤火虫在短时间内产生有节奏的闪光。这种闪光是由于生物发光的一种化学反应，萤火虫的闪光模式因种类而异。萤火虫算法(FA)是基于萤火虫的闪光行为，它是一种用于全局优化问题的智能随机算法，由Yang Xin-She（2009）[1]提出。萤火虫通过下腹的一种化学反应-生物发（bioluminescence）发光。这种生物发光是萤火虫求偶仪式的重要组成部分，也是雄性萤火虫和雌性萤火虫交流的主要媒介，发出光也可用来引诱配偶或猎物，同时这种闪光也有助于保护萤火虫的领地，并警告捕食者远离栖息地。在FA中，认为所有的萤火虫都是雌雄同体的，无论性别如何，它们都互相吸引。该算法的建立基于两个关键的概念：发出的光的强度和两个萤火虫之间产生的吸引力的程度。

2 天然萤火虫的行为
天然萤火虫在寻找猎物、吸引配偶和保护领地时表现出惊人的闪光行为，萤火虫大多生活在热带环境中。一般来说，它们产生冷光，如绿色、黄色或淡红色。萤火虫的吸引力取决于它的光照强度，对于任何一对萤火虫来说，较亮的萤火虫会吸引另一只萤火虫。所以，亮度较低的个体移向较亮的个体，同时光的亮度随着距离的增加而降低。萤火虫的闪光模式可能因物种而异，在一些萤火虫物种中，雌性会利用这种现象猎食其他物种；有些萤火虫在一大群萤火虫中表现出同步闪光的行为来吸引猎物，雌萤火虫从静止的位置观察雄萤火虫发出的闪光，在发现一个感兴趣趣的闪光后，雌性萤火虫会做出反应，发出闪光，求偶仪式就这样开始了。一些雌性萤火虫会产生其他种类萤火虫的闪光模式，来诱捕雄性萤火虫并吃掉它们。

3 萤火虫算法
萤火虫算法模拟了萤火虫的自然现象。真实的萤火虫自然地呈现出一种离散的闪烁模式，而萤火虫算法假设它们总是在发光。为了模拟萤火虫的这种闪烁行为，Yang Xin-She提出了了三条规则（Yang，2009）：
（1）假设所有萤火虫都是雌雄同体的，因此一只萤火虫可能会被其他任何萤火虫吸引。
（2）萤火虫的亮度决定其吸引力的大小，较亮的萤火虫吸引较暗的萤火虫。如果没有萤火虫比被考虑的萤火虫更亮，它就会随机移动。
（3）函数的最优值与萤火虫的亮度成正比。
光强(I)与光源距离（r）服从平方反比定律，因此由于空气的吸收，光的强度(I)随着与光源距离的增加而减小，这种现象将萤火虫的可见性限定在了非常有限的半径内：

萤火虫算法的主要实现步骤如下：

其中I0为距离r=0时的光强（最亮），即自身亮度，与目标函数值有关，目标值越优，亮度越亮；γ为吸收系数，因为荧光会随着距离的增加和传播媒介的吸收逐渐减弱，所以设置光强吸收系数以体现此特性，可设置为常数；r表示两个萤火虫之间的距离。有时也使用单调递减函数，如下式所示。

第二步为种群初始化：

其中t表示代数，xt表示个体的当前位置，β0exp(-γr2)是吸引度，αε是随机项。下一步将会计算萤火虫之间的吸引度：

其中β0表示r=0时的最大吸引度。
下一步，低亮度萤火虫向较亮萤火虫运动：

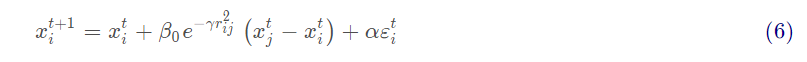
最后一个阶段，更新光照强度，并对所有萤火虫进行排序，以确定当前的最佳解决方案。萤火虫算法的主要步骤如下所示。

Begin
	初始化算法基本参数：设置萤火虫数目n，最大吸引度β0，光强吸收系数γ，步长因子α，最大迭代次数MaxGeneration或搜索精度ε；
	初始化：随机初始化萤火虫的位置，计算萤火虫的目标函数值作为各自最大荧光亮度I0；
	t=1
	while(t<=MaxGeneration || 精度>ε)
		计算群体中萤火虫的相对亮度I(式2)和吸引度β（式5），根据相对亮度决定萤火虫的移动方向；
		更新萤火虫的空间位置，对处在最佳位置的萤火虫进行随机移动（式6）；
		根据更新后萤火虫的位置，重新计算萤火虫的亮度I0；
		t=t+1
	end while
	输出全局极值点和最优个体值。
end


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
 

萤火虫算法与粒子群算法(PSO)和细菌觅食算法(BFA)有相似之处。在位置更新方程中，FA和PSO都有两个主要分量：一个是确定性的，另一个是随机性的。在FA中，吸引力由两个组成部分决定：目标函数和距离，而在BFA中，细菌之间的吸引力也有两个组成部分：适应度和距离。萤火虫算法实现时，整个种群(如n)需要两个内循环，特定迭代需要一个外循环(如I)，因此最坏情况下FA的计算复杂度为O(n2I)。

二、部分源代码

%% Main Function

clc;
clear;   

%% Parameters Setting
w = 100;   
d = 100;   % dimensions of each solutions(firefly)
point = d;  %the sensor point covered by WSN 100*100
% 选择的探测半径
r = 7; % radius of sensor point coverage region in WSN
q = 0;
% 参数意义
para = [25 5 0.7 0.2 1];% parameters [n N_iteration alpha betamin gamma]

Ub = ones(1,d).*w; %/*upper bounds of the parameters. */
Lb = zeros(1,d);   %/*lower bound of the parameters.*/

% Initial random guess
u0=(Lb+Ub)/2; 

%% Wireless Sensor Network Deployment using Fireflies Algorithm
% 函数ffa_wsn为萤火虫算法的实质
[ux,uy,fval,NumEval,maxzn]=ffa_wsn(u0,Lb,Ub,para,q);

%% Results Visualization
draw(ux, uy, 100, 7)
bestsolutionx = ux;
bestsolutiony = uy;
bestojb = fval
total_number_of_function_evaluations = NumEval

function [nsx,nsy] = ffa_move(n, nsx, nsy, Lightn, nsxo, nsyo, Lighto, alpha, betamin, gamma, b)
%% Move all fireflies toward brighter ones
% optional extra parameters: (Lb, Ub, nxbest, nybest,Lightbest) 
% Note:
% the ways of updating solution are strongly encouraged to overwrite,
% because the original one is time consuming,
% a simple way is to update solution randomly,
% but ensure the new coverage after updated should be better,
% otherwise, do not update 
%
 
% ==================================

%%
% Scaling of the system
% scale=abs(Ub-Lb);

% Updating fireflies
for i = 1:n,
% The attractiveness parameter beta=exp(-gamma*r)
   for j = 1:n,
  
    k = randi([1, 100],1,1);
	l = randi([1, 100],1,1);
	rx = abs(nsx(i,k) - nsx(j,l));
	ry = abs(nsy(i,k) - nsy(j,l)); 
	
	rx1 = abs(nsx(i,l) - nsx(j,k));
	ry1 = abs(nsy(i,l) - nsy(j,k));
	
   % r=sqrt(sum((nsx(i,:)-nsx(j,:)).^2)+(nsy(i,:)-nsy(j,:)).^2);  %r^2=||xi-xj||^2+||yi-yj||^2
   % Update moves
    
   if Lightn(i) < Lighto(j), % Brighter and more attractive
  
   % ================= original ==========================
   % beta0 = 1; 
   % beta = (beta0 - betamin)*exp(-gamma*r.^2) + betamin; 
   % b = beta0 - betamin
   % ====================================================

   %% Update Solution
   % TODO: NEED TO BE REPLACED WITH OTHER UPDATE METHOD
   betax = b*exp(-gamma*rx.^2) + betamin; 
   betay = b*exp(-gamma*ry.^2) + betamin;
   
   betax1 = b*exp(-gamma*rx1.^2) + betamin; 
   betay1 = b*exp(-gamma*ry1.^2) + betamin;
  
   tmpf = alpha.*(rand(1,1) - 0.5);%.*scale; 
   nsx(i,k) = nsx(i,k).*(1-betax) + nsxo(j,l).*betax + tmpf;
   nsy(i,k) = nsy(i,k).*(1-betay) + nsyo(j,l).*betay + tmpf;
   
   nsx(i,l) = nsx(i,l).*(1-betax1) + nsxo(j,k).*betax + tmpf;
   nsy(i,l) = nsy(i,l).*(1-betay1) + nsyo(j,k).*betay + tmpf;
   
   Solution_temp = [nsx(i,:);nsy(i,:)];   
   Lightn_temp = coverage(Solution_temp,100,7);
   
   if Lightn_temp < Lightn(i)  %lightness didn't be improved
      nsx(i,:) = nsxo(i,:);
	  nsy(i,:) = nsyo(i,:);
	  
   else Lightn(i) = Lightn_temp;
       Lighto(i) = Lightn(i);
	 end
	end
   end % end for j
end % end for i
function [nxbest,nybest,fbest,NumEval,maxzn]...
           = ffa_wsn(u0, Lb, Ub, para,q)
%% Check input parameters (otherwise set as default values)
%if nargin<6, 
%para=[20 150 0.25 0.20 1];
%end
%if nargin<5, Ub=[]; end
%if nargin<4, Lb=[]; end
%if nargin<3,
%disp('Usuage: FA_wsn(u0,Lb,Ub,para)');
%end
% n=number of fireflies
% MaxGeneration=number of pseudo time steps
% ------------------------------------------------
% alpha=0.25;      % Randomness 0--1 (highly random)
% betamn=0.20;     % minimum value of beta
% gamma=1;         % Absorption coefficient
% ------------------------------------------------
% @author: Shangru Zhong
% @email: draco.mystack@gmail.com
% @date: 11/01/2013
% ==================================

%% 先前para数组中各个参数的含义
% 萤火虫数目
n = para(1);
% 迭代次数
MaxGeneration = para(2);
% 步长因子
alpha = para(3); 
% 待理解
betamin = para(4); 
gamma = para(5);
beta0 = 1; 
b = beta0-betamin;
NumEval = n*MaxGeneration;% Total number of function evaluations


    disp('Simple bounds/limits are improper!');
    return
end

% Calcualte dimension
d = length(u0);   

% Initial values of an array
zn = ones(n, 1);
% ------------------------------------------------
% generating the initial locations of n fireflies
% 初始化萤火虫位置
[nsx, nsy, Lightn] = init_ffa(n, d, Lb, Ub, u0);

% Iterations or pseudo time marching
for iter = 1:MaxGeneration,     

 2*100
   zn(i) = coverage(Solution,100,7); % WSN coverage of solution i (with points 100 and radius 7)  
   Lightn(i) = zn(i);   
end
maxzn(q) = max(zn);
disp(['coverage of current solution: ', num2str(maxzn(q))])
% minzn(a)=min(zn)

%% Find the current best
nsxo = nsx; 
nsyo = nsy;
Lighto = Lightn;

% Move all fireflies to the better locations
[nsx,nsy] = ffa_move(n, nsx, nsy, Lightn, nsxo, nsyo, Lighto, alpha, betamin, gamma, b);%Lb,Ub);
      
end   % end of iterations 

% Ranking fireflies by their light intensity/objectives
[Lightn,Index] = sort(zn);

 nxbest = nsx(n,:); 
 nybest = nsy(n,:);
 Lightbest = Lightn(n);
 fbest = Lightbest;
% Check if the updated solutions/locations are within limits
[nsx, nsy] = findlimits(n, nsx, nsy, Lb, Ub);


function alpha = alpha_new(alpha, NGen)
% alpha_n=alpha_0(1-delta)^NGen=0.005
% alpha_0=0.9
delta=1-(0.005/0.9)^(1/NGen);
alpha=(1-delta)*alpha;



  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
  
144
  
145
  
146
  
147
  
148
  
149
  
150
  
151
  
152
  
153
  
154
  
155
  
156
  
157
  
158
  
159
  
160
  
161
  
162
  
163
  
164
  
165
  
166
  
167
  
168
  
169
  
170
  
171
  
172
  
173
  
174
  
175
  
176
  
177
  
178
  
179
  
180
  
181
  
182
  
183
  
184
  
185
  
186
  
187
  
188
  
189
  
190
  
191
  
192
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]群体智能优化算法之萤火虫算法(Firefly Algorithm，FA)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/120063674