【优化算法】混沌单纯形法算子布谷鸟搜索优化算法【含Matlab源码 1193期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【优化算法】混沌单纯形法算子布谷鸟搜索优化算法【含Matlab源码 1193期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、布谷鸟算法简介

1 介绍
布谷鸟（杜鹃）是一种非常迷人的鸟类，它们不仅能发出各种声音或叫声，还能以不同的方式繁殖。杜鹃科中的犀鹃（Ani Cuckoo）和圭拉鹃（Guira Cuckoo），将它们的蛋放在其他鸟的巢中，从此杜鹃鸟的蛋完全依赖于寄主鸟的照料，这就是巢寄生。

如果寄主鸟发现蛋不是它们的，要么把蛋扔掉，要么放弃巢穴，然后寄主鸟再建一个新的巢穴。为了防止这种情况的发生，雌性布谷鸟已经进化到可以模拟寄主蛋的颜色和纹理，从而降低被遗弃的可能性。同时蛋也会分布在不同的巢中，以减少蛋丢失的机会。如果布谷鸟的蛋没有被识别出来，它通常会在寄主鸟蛋之前孵化，并把其他的蛋从巢中踢出去，这样就能分得更多的食物，甚至有些布谷鸟雏鸟也能模仿寄主雏鸟的叫声。

巢寄生的一个好处是，父母不需要投资筑巢或喂养幼鸟。他们可以花更多的时间在捕食和繁殖上。随着时间的推移，自然选择使寄主鸟和布谷鸟都进化了，使得每一代中最适合的鸟存活下来。布谷鸟的这种繁殖行为是协同进化的最佳模型之一，也是最近发展的优化技术，即布谷鸟搜索的基础。

2 人工布谷鸟搜索
布谷鸟搜索受布谷鸟的巢寄生行为和一些鸟类和果蝇的莱维（Lévy Flight）行为的启发，是由Xin-She Yang和Suash Deb (2009)[2]提出的一种新型的基于群体的优化技术。

布谷鸟算法源于以下三条规则[3]：
每只布谷鸟每次产下一枚蛋，并将其放入随机选择的巢中；
具有优质蛋的最佳巢会被进入到下一代；
可用的寄主巢数量是固定的，且寄主以概率pa∈(0,1)发现布谷鸟放的蛋。在这种情况下，寄主可以消灭该蛋或放弃旧巢另建新巢。
在进一步研究算法之前，先讨论一些数学术语和函数。

2.1 随机变量
任何随机现象的输出都是随机变量，并用X表示。如果一个随机变量只取不同的值，比如1,2，那么它就是离散的；如果它可以在一个区间内取任意值，那它就是连续的。这些通常用曲线下的面积或积分表示。随机变量X在一组结果A上的概率，就是A上和曲线下之间的面积，这条曲线下的总面积必须是1，对于集合A中的任何元素都不应该有负值。这样的曲线称为密度曲线。

2.2 随机游走
随机游走（记为SN）是一系列随机步的和，每一步都由一个随机变量Xi表达：

随机游走的长度可以是固定的，也可以是可变的(取决于步长)。

2.2.1 幂律
当一个量相对变化时会导致两一个量成比例的相对变化时，需要应用幂律（比例律），幂律分布的一般形式是：

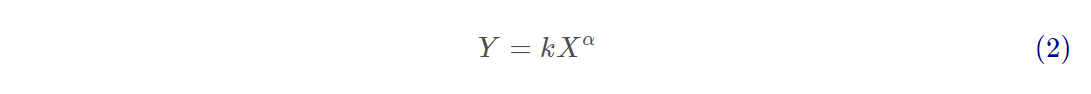
其中X和Y是目标变量，α是律指数，k为常量。

2.3 赫维赛德函数（阶跃函数）
通常用H或θ表示，用于表达分段常数函数或广义函数。
作为分段函数时：

2.4 Lévy（莱维）分布
Lévy分布是非负随机变量的稳定连续概率分布，可以用以下简单的方式表达：

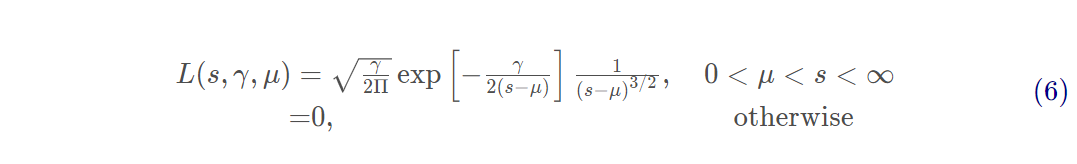
其中µ是最小步长，γ是尺度参数。

6.2.4.1 Lévy飞行
Lévy飞行是步长服从Lévy分布的随机游走，通过下式表达：

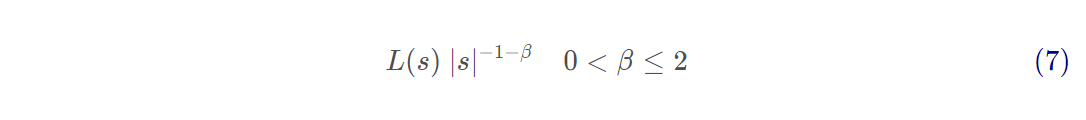
其中β是一个索引。

三、部分源代码

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% % % % % % CLSCS算法核心---% % % % % %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [ keepglobal] = Cuckoo_search( popsize,pa,xMin,xMax,iter_max,dim,fun )

     LB=xMin*ones(1,dim);
     UB=xMax*ones(1,dim);
     u=3;%混沌系数

    fitness=inf*ones(popsize,1); %初始化适应度值
    
    %随机的初始值
    for i=1:popsize,
        nest(i,:)=LB+(UB-LB).*rand(size(LB));
    end
    
    %得到当前最优解
    [fbest,bestnest,nest,fitness]=get_best_nest(nest,nest,fitness,fun);
    keepglobal(1)=fbest;
    
    fprintf('Run = %d Save_Nr_best = %e\n', 1, fbest);
  
    %%开始循环
    for i=2:iter_max
        %产生新的解（但保留当前最优的）
        new_nest=get_cuckoos(nest,bestnest,LB,UB,iter_max,i);
        %单纯形法--去除较差的鸟窝
        new_nest=dcxf(popsize,new_nest,fun);
        
        [f_min,best,nest,fitness]=get_best_nest(nest,new_nest,fitness,fun);
        
    
   
        %发现并随机选择
        new_nest=empty_nests(nest,LB,UB,pa,iter_max,i,fitness);


        %评价改解
        [f_min,best,nest,fitness]=get_best_nest(nest,new_nest,fitness,fun);
        
% % % % % % % % % % % % % % % % % % % % % % % % % % % % %         
       %%对粒子群最优位置进行混沌优化
      y(1,:)=(best-xMin)/(xMax-xMin);% 将最优位置映射到Logistic方程的定义域[0,1]
      fitness_c(1)=func(y(1,:),fun); 
        for t=1:popsize-1 %通过Logistic方程进行M次迭代，得到混沌序列
            for e=1:dim
                 y(t+1,e)=u*y(t,e)*(1-y(t,e)); 
            end
              y(t+1,:)=xMin+(xMax-xMin)*y(t+1,:);%将混沌序列逆射到原解空间
             fitness_c(t+1)=func(y(t+1,:),fun); %计算混沌变量可行解序列的适应度值
        end
        [ybestfitness ybestindex]=min(fitness_c);%寻找最优混沌可行解矢量
        
        if ybestfitness<f_min
            f_min=ybestfitness;
            best=y(ybestindex,:);
        end
        function [fit] = func(x, fun)
%benchmark functions

% Developed by: Dr. Mahamed G.H. Omran (omran.m@gust.edu.kw) 12-May-2011
% Modified and improved by: Maurice Clerc (15-May-2011)

% x is a D-dimensional vector representing the solution we want to evalaute
% fun is the indix of the function of interest
% fit is the fitness of x (i.e. fit = f(x))

D = length(x);

switch(fun)
%     case {1,2,3,4,5,6,7,8,9,10,11,12,13,14}, % CEC'05 functions
        % NOTE:
        % For these functions to work, you need to include the following
        % lines in your file:
        % global  initial_flag
        % initial_flag = 0;
        % In addition, vector x should be x(1,D) where D is the problem's
        % dimension
%         fit = benchmark_func(x, fun);
    case {1}, % Sphere function
        fit = sum(x.^2);
    case {2}, % Rastrigin
        fit = 10*D + sum(x.^2 - 10*cos(2.*pi.*x));
    case {3}, %Step
        fit = sum(floor(x + 0.5).^2);
    case {4}, %Rosenbrock
        f = 0;
        for i = 1:1:D-1
            f = f + 100*((x(i+1) - x(i)^2)^2) + (1 - x(i))^2;
        end
        fit = f;
    case {5}, %Ackley
       fit = -20*exp(-0.2*sqrt(sum(x.^2)/D)) - exp(sum(cos(2*pi .*x))/D) + 20 + exp(1);
    case {6}, %Griewank
        sum1 = 0;
        prod1 = 1;
        for i = 1:1:D
            sum1 = sum1 + (x(i)^2/4000);
            prod1 = prod1*cos(x(i)/sqrt(i));
        end
        fit = sum1 - prod1 + 1;
    case {7}, %Salomon
        fit = -cos(2*pi*sqrt(sum(x.^2))) + 0.1*sqrt(sum(x.^2)) + 1;
    case {8}, %Quartic function
        sum1 = 0;
        for i = 1:1:D
            sum1 = sum1 + i*x(i)^4;
        end
        fit = sum1 + rand();
    case {9}, %Alpine
        sum1 = 0;
        for i=1:1:D
            sum1 = sum1 + abs(x(i)*sin(x(i)) + 0.1*x(i));
        end
        fit = sum1;
   case {10}, %Six Hump Camel bsck
        fit = 4*x(1).^2 - 2.1*x(1).^4 + (1/3)*x(1).^6 + x(1)*x(2) - 4*x(2)^2 + 4*x(2).^4;
    case {11}, % Branin
        fit = (x(2)-(5.1/(4*pi^2))*x(1)^2+5*x(1)/pi-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
    case {12}, % Shubert
        sum0 = 0;
        sum1 = 0;
        for j=1:1:5
            sum0 = sum0 + j*cos((j+1)*x(1) + j);
            sum1 = sum1 + j*cos((j+1)*x(2) + j);
        end
        fit = sum0*sum1;
    case {13}, % Easom
        fit = -cos(x(1))*cos(x(2))*exp(-((x(1) - pi)^2 + (x(2) - pi)^2));
    case {14}, % Shekel function
% Matlab Code by A. Hedar (Nov. 23, 2005).
% The number of variables n = 4
% The parameter m should be adjusted m = 5,7,10.
% The default value of m = 10.
% 
m = 10;
a = ones(10,4);
a(1,:) = 4.0*a(1,:);
a(2,:) = 1.0*a(2,:);
a(3,:) = 8.0*a(3,:);
a(4,:) = 6.0*a(4,:);
for j = 1:2;
   a(5,2*j-1) = 3.0; a(5,2*j) = 7.0; 
   a(6,2*j-1) = 2.0; a(6,2*j) = 9.0; 
   a(7,j)     = 5.0; a(7,j+2) = 3.0;
   a(8,2*j-1) = 8.0; a(8,2*j) = 1.0;
   a(9,2*j-1) = 6.0; a(9,2*j) = 2.0;
   a(10,2*j-1)= 7.0; a(10,2*j)= 3.6;
end
c(1) = 0.1; c(2) = 0.2; c(3) = 0.2; c(4) = 0.4; c(5) = 0.4;
c(6) = 0.6; c(7) = 0.3; c(8) = 0.7; c(9) = 0.5; c(10)= 0.5;
s = 0;
for j = 1:m;
   p = 0;
   for i = 1:4
      p = p+(x(i)-a(j,i))^2;
   end
   s = s+1/(p+c(j));
end
fit = -s;

    otherwise,
        error('No such function');
        fit = -1;
end

% fit=abs(fit-opt_f);

end


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
  
144
  
145
  
146
  
147
  
148
  
149
  
150
  
151
  
152
  
153
  
154
  
155
  
156
  
157
  
158
  
159
  
160
  
161
  
162
  
163
  
164
  
165
  
166
  
167
  
168
  
169
  
170
 

四、运行结果

五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/119493065