【LSTM时间序列预测】基于matlab贝叶斯网络优化LSTM时间序列预测【含Matlab源码 1329期】

一、贝叶斯网络及LSTM简介

1 贝叶斯网络
贝叶斯网络(Bayesian network)，又称信念网络(Belief Network)，或有向无环图模型(directed acyclic graphical model)，是一种概率图模型，于1985年由Judea Pearl首先提出。它是一种模拟人类推理过程中因果关系的不确定性处理模型，其网络拓朴结构是一个有向无环图(DAG)。

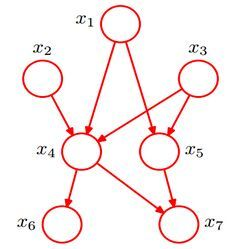
贝叶斯网络的有向无环图中的节点表示随机变量{ X 1 , X 2 , . . . , X n }
它们可以是可观察到的变量，或隐变量、未知参数等。认为有因果关系（或非条件独立）的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(children)”，两节点就会产生一个条件概率值。
例如，假设节点E直接影响到节点H，即E→H，则用从E指向H的箭头建立结点E到结点H的有向弧(E,H)，权值(即连接强度)用条件概率P(H|E)来表示，如下图所示：

简言之，把某个研究系统中涉及的随机变量，根据是否条件独立绘制在一个有向图中，就形成了贝叶斯网络。其主要用来描述随机变量之间的条件依赖，用圈表示随机变量(random variables)，用箭头表示条件依赖(conditional dependencies)。
此外，对于任意的随机变量，其联合概率可由各自的局部条件概率分布相乘而得出：

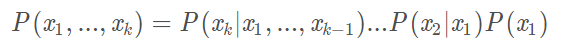
2.4.1 贝叶斯网络的结构形式
（1） head-to-head

依上图，所以有：P(a,b,c) = P(a)*P(b)P(c|a,b)成立，即在c未知的条件下，a、b被阻断(blocked)，是独立的，称之为head-to-head条件独立。
（2） tail-to-tail

考虑c未知，跟c已知这两种情况：
在c未知的时候，有：P(a,b,c)=P©P(a|c)P(b|c)，此时，没法得出P(a,b) = P(a)P(b)，即c未知时，a、b不独立。
在c已知的时候，有：P(a,b|c)=P(a,b,c)/P©，然后将P(a,b,c)=P©P(a|c)P(b|c)带入式子中，得到：P(a,b|c)=P(a,b,c)/P© = P©P(a|c)*P(b|c) / P© = P(a|c)*P(b|c)，即c已知时，a、b独立。
（3）head-to-tail

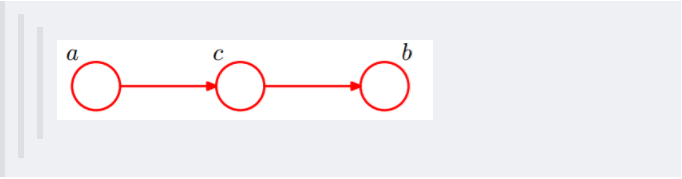
还是分c未知跟c已知这两种情况：
c未知时，有：P(a,b,c)=P(a)*P(c|a)*P(b|c)，但无法推出P(a,b) = P(a)P(b)，即c未知时，a、b不独立。
c已知时，有：P(a,b|c)=P(a,b,c)/P©，且根据P(a,c) = P(a)P(c|a) = P©P(a|c)，可化简得到：

所以，在c给定的条件下，a，b被阻断(blocked)，是独立的，称之为head-to-tail条件独立。
这个head-to-tail其实就是一个链式网络，如下图所示：

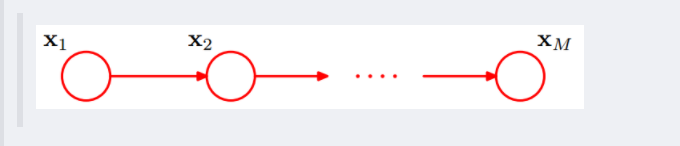
根据之前对head-to-tail的讲解，我们已经知道，在xi给定的条件下，xi+1的分布和x1,x2…xi-1条件独立。意味着啥呢？意味着：xi+1的分布状态只和xi有关，和其他变量条件独立。通俗点说，当前状态只跟上一状态有关，跟上上或上上之前的状态无关。这种顺次演变的随机过程，就叫做马尔科夫链（Markov chain）。对于马尔科夫链我们下一节再细讲。

2 LSTM简介
2.1 LSTM控制流程
LSTM的控制流程：是在前向传播的过程中处理流经细胞的数据，不同之处在于 LSTM 中细胞的结构和运算有所变化。

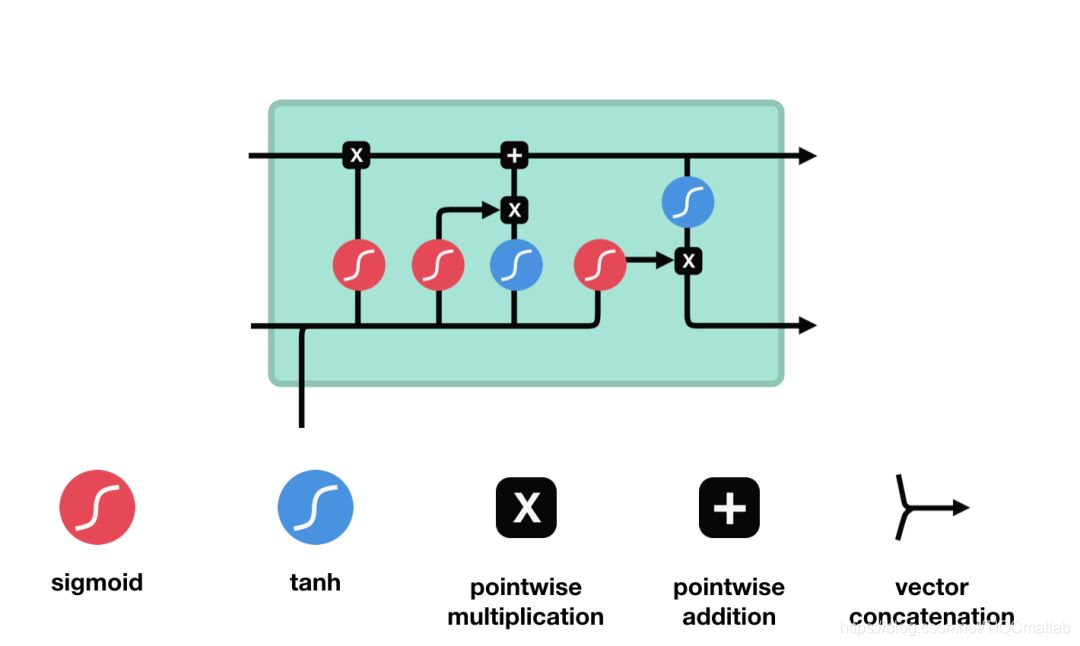
这一系列运算操作使得 LSTM具有能选择保存信息或遗忘信息的功能。咋一看这些运算操作时可能有点复杂，但没关系下面将带你一步步了解这些运算操作。

2.2 核心概念
LSTM 的核心概念在于细胞状态以及“门”结构。细胞状态相当于信息传输的路径，让信息能在序列连中传递下去。你可以将其看作网络的“记忆”。理论上讲，细胞状态能够将序列处理过程中的相关信息一直传递下去。
因此，即使是较早时间步长的信息也能携带到较后时间步长的细胞中来，这克服了短时记忆的影响。信息的添加和移除我们通过“门”结构来实现，“门”结构在训练过程中会去学习该保存或遗忘哪些信息。

2.3 Sigmoid
门结构中包含着 sigmoid 激活函数。Sigmoid 激活函数与 tanh 函数类似，不同之处在于 sigmoid 是把值压缩到 0~1 之间而不是 -1~1 之间。这样的设置有助于更新或忘记信息，因为任何数乘以 0 都得 0，这部分信息就会剔除掉。同样的，任何数乘以 1 都得到它本身，这部分信息就会完美地保存下来。这样网络就能了解哪些数据是需要遗忘，哪些数据是需要保存。

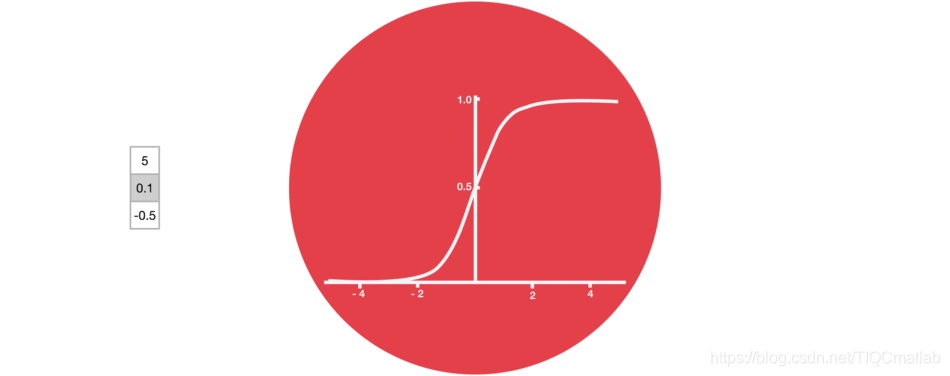
2.4 LSTM门结构
LSTM 有三种类型的门结构：遗忘门、输入门和输出门。
2.4.1 遗忘门
遗忘门的功能是决定应丢弃或保留哪些信息。来自前一个隐藏状态的信息和当前输入的信息同时传递到 sigmoid 函数中去，输出值介于 0 和 1 之间，越接近 0 意味着越应该丢弃，越接近 1 意味着越应该保留。

2.4.2 输入门
输入门用于更新细胞状态。首先将前一层隐藏状态的信息和当前输入的信息传递到 sigmoid 函数中去。将值调整到 0~1 之间来决定要更新哪些信息。0 表示不重要，1 表示重要。
其次还要将前一层隐藏状态的信息和当前输入的信息传递到 tanh 函数中去，创造一个新的侯选值向量。最后将 sigmoid 的输出值与 tanh 的输出值相乘，sigmoid 的输出值将决定 tanh 的输出值中哪些信息是重要且需要保留下来的。

2.4.3 细胞状态
下一步，就是计算细胞状态。首先前一层的细胞状态与遗忘向量逐点相乘。如果它乘以接近 0 的值，意味着在新的细胞状态中，这些信息是需要丢弃掉的。然后再将该值与输入门的输出值逐点相加，将神经网络发现的新信息更新到细胞状态中去。至此，就得到了更新后的细胞状态。

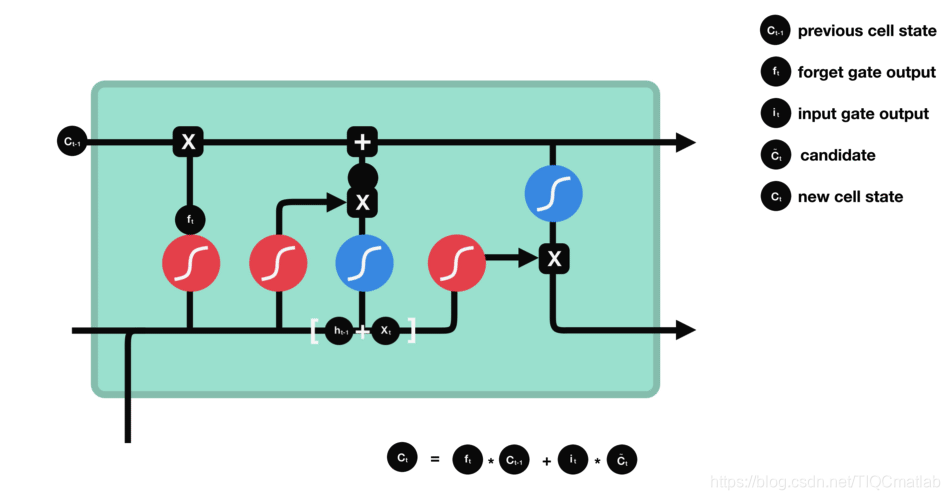
2.4.4 输出门
输出门用来确定下一个隐藏状态的值，隐藏状态包含了先前输入的信息。首先，我们将前一个隐藏状态和当前输入传递到 sigmoid 函数中，然后将新得到的细胞状态传递给 tanh 函数。
最后将 tanh 的输出与 sigmoid 的输出相乘，以确定隐藏状态应携带的信息。再将隐藏状态作为当前细胞的输出，把新的细胞状态和新的隐藏状态传递到下一个时间步长中去。

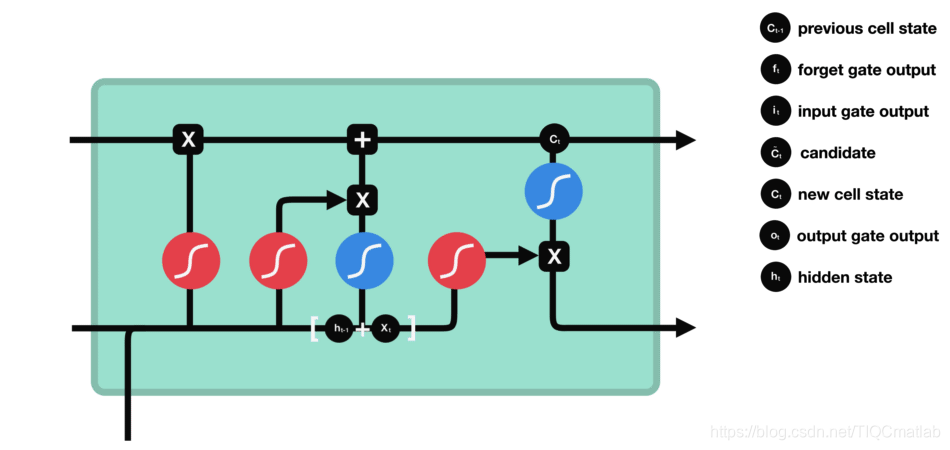
让我们再梳理一下。遗忘门确定前一个步长中哪些相关的信息需要被保留；输入门确定当前输入中哪些信息是重要的，需要被添加的；输出门确定下一个隐藏状态应该是什么。

二、部分源代码

clc; clear; close all;
%% ---------------------------- init Variabels ----------------------------
opt.Delays = 1:30;
opt.dataPreprocessMode  = 'Data Standardization'; % 'None' 'Data Standardization' 'Data Normalization'
opt.learningMethod      = 'LSTM';
opt.trPercentage        = 0.80;                   %  divide data into Test  and Train dataset

% ---- General Deep Learning Parameters(LSTM and CNN General Parameters)
opt.maxEpochs     = 400;                         % maximum number of training Epoch in deeplearning algorithms.
opt.miniBatchSize = 32;                         % minimum batch size in deeplearning algorithms .
opt.executionEnvironment = 'cpu';                % 'cpu' 'gpu' 'auto'
opt.LR                   = 'adam';               % 'sgdm' 'rmsprop' 'adam'
opt.trainingProgress     = 'none';  % 'training-progress' 'none'

% ------------- BILSTM parameters
opt.isUseBiLSTMLayer  = true;                     % if it is true the layer turn to the Bidirectional-LSTM and if it is false it will turn the units to the simple LSTM
opt.isUseDropoutLayer = true;                    % dropout layer avoid of bieng overfit
opt.DropoutValue      = 0.5;

% ------------ Optimization Parameters
opt.optimVars = [
    optimizableVariable('NumOfLayer',[1 4],'Type','integer')
    optimizableVariable('NumOfUnits',[50 200],'Type','integer')
    optimizableVariable('isUseBiLSTMLayer',[1 2],'Type','integer')
    optimizableVariable('InitialLearnRate',[1e-2 1],'Transform','log')
    optimizableVariable('L2Regularization',[1e-10 1e-2],'Transform','log')];

opt.isUseOptimizer         = true;

opt.MaxOptimizationTime    = 14*60*60;
opt.MaxItrationNumber      = 60;
opt.isDispOptimizationLog  = true;

opt.isSaveOptimizedValue       = false;        %  save all of Optimization output on mat files 
opt.isSaveBestOptimizedValue   = true;         %  save Best Optimization output oد a mat file  


%% --------------- load Data
data = loadData(opt);
if ~data.isDataRead
    return;
end

%% --------------- Prepair Data
[opt,data] = PrepareData(opt,data);

%% --------------- Find Best LSTM Parameters with Bayesian Optimization
[opt,data] = OptimizeLSTM(opt,data);

%% --------------- Evaluate Data
[opt,data] = EvaluationData(opt,data);



%% ---------------------------- Local Functions ---------------------------
function data = loadData(opt)
[chosenfile,chosendirectory] = uigetfile({'*.xlsx';'*.csv'},...
    'Select Excel time series Data sets','data.xlsx');
filePath = [chosendirectory chosenfile];
if filePath ~= 0
    data.DataFileName = chosenfile;
    data.CompleteData = readtable(filePath);
    if size(data.CompleteData,2)>1
        warning('Input data should be an excel file with only one column!');
        disp('Operation Failed... '); pause(.9);
        disp('Reloading data. ');     pause(.9);
        data.x = [];
        data.isDataRead = false;
        return;
    end
    data.seriesdataHeder = data.CompleteData.Properties.VariableNames(1,:);
    data.seriesdata = table2array(data.CompleteData(:,:));
    disp('Input data successfully read.');
    data.isDataRead = true;
    data.seriesdata = PreInput(data.seriesdata);
    
    figure('Name','InputData','NumberTitle','off');
    plot(data.seriesdata); grid minor;
    title({['Mean = ' num2str(mean(data.seriesdata)) ', STD = ' num2str(std(data.seriesdata)) ];});
    if strcmpi(opt.dataPreprocessMode,'None')
        data.x = data.seriesdata;
    elseif strcmpi(opt.dataPreprocessMode,'Data Normalization')
        data.x = DataNormalization(data.seriesdata);
        figure('Name','NormilizedInputData','NumberTitle','off');
        plot(data.x); grid minor;
        title({['Mean = ' num2str(mean(data.x)) ', STD = ' num2str(std(data.x)) ];});
    elseif strcmpi(opt.dataPreprocessMode,'Data Standardization')
        data.x = DataStandardization(data.seriesdata);
        figure('Name','NormilizedInputData','NumberTitle','off');
        plot(data.x); grid minor;
        title({['Mean = ' num2str(mean(data.x)) ', STD = ' num2str(std(data.x)) ];});
    end
    
else
    warning(['In order to train network, please load data.' ...
        'Input data should be an excel file with only one column!']);
    disp('Operation Cancel.');
    data.isDataRead = false;
end
end
function data = PreInput(data)
if iscell(data)
    for i=1:size(data,1)
        for j=1:size(data,2)
            if strcmpi(data{i,j},'#NULL!')
                tempVars(i,j) = NaN; %#ok
            else
                tempVars(i,j) = str2num(data{i,j});   %#ok
            end
        end
    end
    data = tempVars;
end
end
function vars = DataStandardization(data)
for i=1:size(data,2)
    x.mu(1,i)   = mean(data(:,i),'omitnan');
    x.sig(1,i)  = std (data(:,i),'omitnan');
    vars(:,i) = (data(:,i) - x.mu(1,i))./ x.sig(1,i);
end
end
function vars = DataNormalization(data)
for i=1:size(data,2)
    vars(:,i) = (data(:,i) -min(data(:,i)))./ (max(data(:,i))-min(data(:,i)));
end
end
% --------------- data preparation for LSTM ---
function [opt,data] = PrepareData(opt,data)
% prepare delays for time serie network
data = CreateTimeSeriesData(opt,data);

% divide data into test and train data
data = dataPartitioning(opt,data);

% LSTM data form
data = LSTMInput(data);
end

% ----Run Bayesian Optimization Hyperparameters for LSTM Network Parameters
function [opt,data] = OptimizeLSTM(opt,data)
if opt.isDispOptimizationLog
    isLog = 2;
else
    isLog = 0;
end
if opt.isUseOptimizer
    opt.ObjFcn  = ObjFcn(opt,data);
    BayesObject = bayesopt(opt.ObjFcn,opt.optimVars, ...
        'MaxTime',opt.MaxOptimizationTime, ...
        'IsObjectiveDeterministic',false, ...
        'MaxObjectiveEvaluations',opt.MaxItrationNumber,...
        'Verbose',isLog,...
        'UseParallel',false);
end
end

% ---------------- objective function
function ObjFcn = ObjFcn(opt,data)
ObjFcn = @CostFunction;

function [valError,cons,fileName] = CostFunction(optVars)
inputSize    = size(data.X,1);
outputMode   = 'last';
numResponses = 1;
dropoutVal   = .5;

if optVars.isUseBiLSTMLayer == 2
    optVars.isUseBiLSTMLayer = 0;
end

if opt.isUseDropoutLayer % if dropout layer is true
    if optVars.NumOfLayer ==1
        if optVars.isUseBiLSTMLayer
            opt.layers = [ ...
                sequenceInputLayer(inputSize)
                bilstmLayer(optVars.NumOfUnits,'OutputMode',outputMode)
                dropoutLayer(dropoutVal)
                fullyConnectedLayer(numResponses)
                regressionLayer];
        else
            opt.layers = [ ...
                sequenceInputLayer(inputSize)
                lstmLayer(optVars.NumOfUnits,'OutputMode',outputMode)
                dropoutLayer(dropoutVal)
                fullyConnectedLayer(numResponses)
                regressionLayer];
        end
    elseif optVars.NumOfLayer==2
        if optVars.isUseBiLSTMLayer
            opt.layers = [ ...
                sequenceInputLayer(inputSize)
                bilstmLayer(optVars.NumOfUnits,'OutputMode','sequence')
                dropoutLayer(dropoutVal)
                bilstmLayer(optVars.NumOfUnits,'OutputMode',outputMode)
                dropoutLayer(dropoutVal)
                fullyConnectedLayer(numResponses)
                regressionLayer];
        else
            opt.layers = [ ...
                sequenceInputLayer(inputSize)
                lstmLayer(optVars.NumOfUnits,'OutputMode','sequence')
                dropoutLayer(dropoutVal)
                lstmLayer(optVars.NumOfUnits,'OutputMode',outputMode)
                dropoutLayer(dropoutVal)
                fullyConnectedLayer(numResponses)
                regressionLayer];
        end
 

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
  
144
  
145
  
146
  
147
  
148
  
149
  
150
  
151
  
152
  
153
  
154
  
155
  
156
  
157
  
158
  
159
  
160
  
161
  
162
  
163
  
164
  
165
  
166
  
167
  
168
  
169
  
170
  
171
  
172
  
173
  
174
  
175
  
176
  
177
  
178
  
179
  
180
  
181
  
182
  
183
  
184
  
185
  
186
  
187
  
188
  
189
  
190
  
191
  
192
  
193
  
194
  
195
  
196
  
197
  
198
  
199
  
200
  
201
  
202
  
203
  
204
  
205
  
206
  
207
  
208
 

三、运行结果

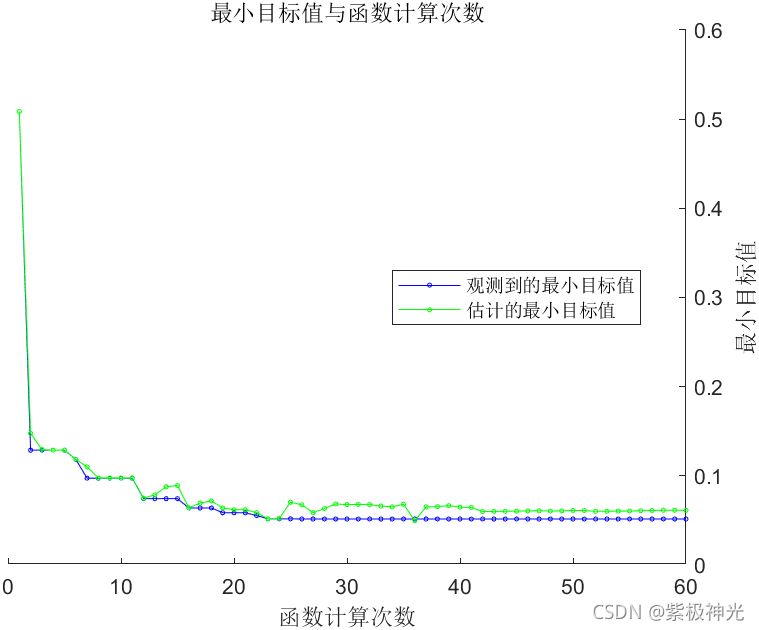
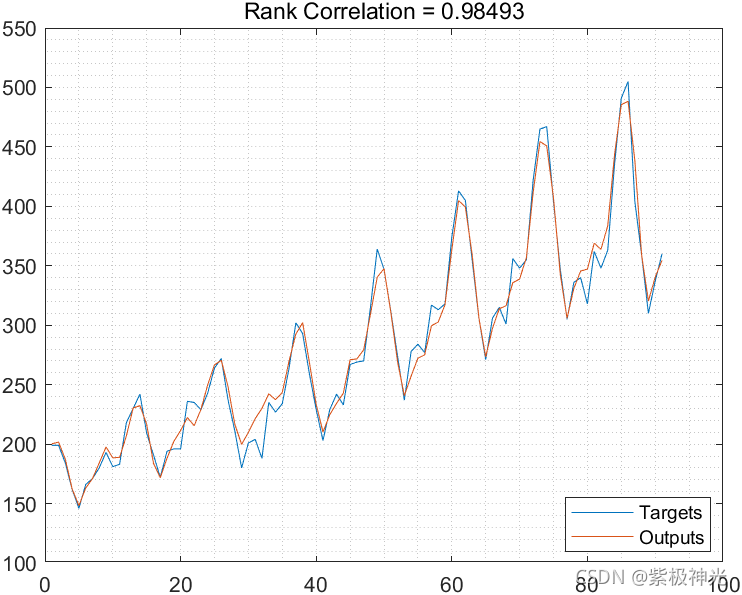
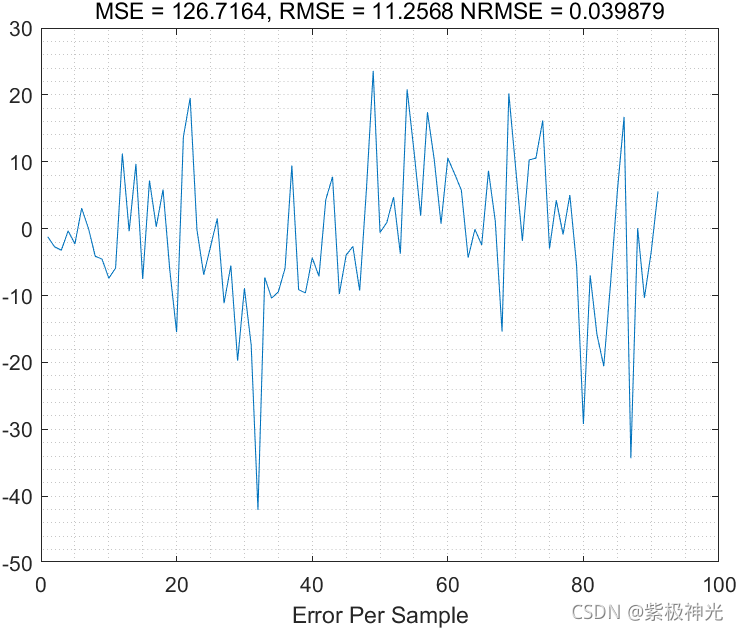
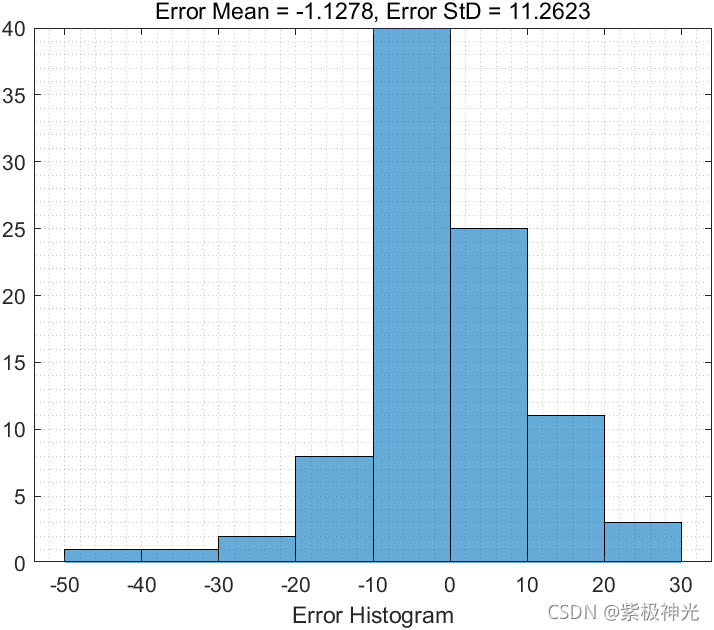
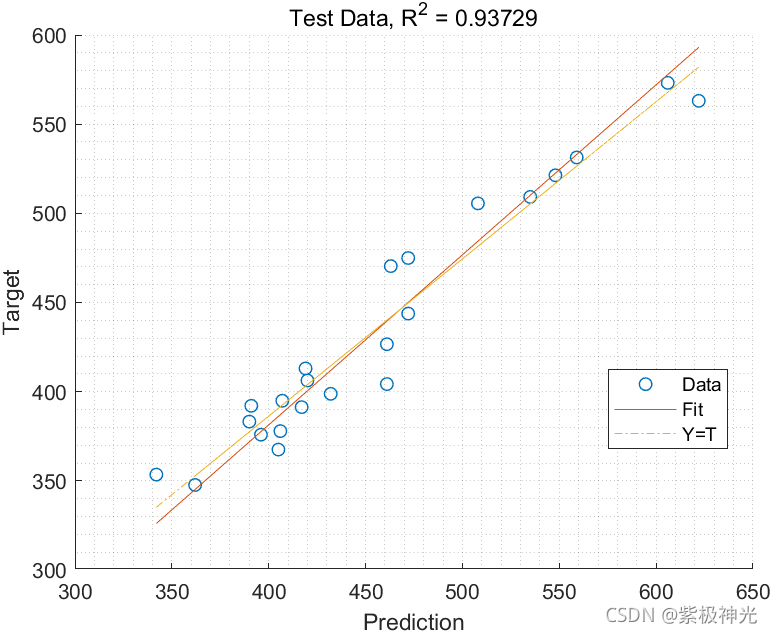
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/120472076