【优化算法】差分松鼠搜索优化算法（DSSA）【含Matlab源码 1330期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【优化算法】差分松鼠搜索优化算法（DSSA）【含Matlab源码 1330期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、差分松鼠搜索优化算法简介

提出了一种新的混合差分松鼠搜索算法优化算法(dssa) ，该算法将松鼠搜索算法的搜索方法和差异进化算法优化过程相结合，用于求解全局最佳化问题。主要研究内容包括引入差异进化算法算法中的交叉机制，提高算法的搜索能力，改进松鼠觅食过程中的更新规则，提高算法的利用能力。

三、部分源代码

% Differential Squirrel Search Algorithm (DSSA) source Code Version 1.0


clearvars
close all
clc

disp('The DSSA is tracking the problem');

N=30; % Number of Squirrel
Function_name='F23' % Name of the test function that can be from F1 to F23 
MaxIT=500; % Maximum number of iterations

[lb,ub,dim,fobj]=Get_Functions_details(Function_name); % Function details

Times=11; %Number of independent times you want to run the DSSA
display(['Number of independent runs: ', num2str(Times)]);

for i=1:Times
[Destination_fitness(i),bestPositions(i,:),Convergence_curve(i,:)]=DSSA(N,MaxIT,lb,ub,dim,fobj);
display(['The optimal fitness of DSSA is: ', num2str(Destination_fitness(i))]);
end

[bestfitness,index]=min(Destination_fitness);
disp('--------Best Fitness, Average Fitness, Standard Deviation and Best Solution--------');
display(['The best fitness of DSSA is: ', num2str(bestfitness)]);
display(['The average fitness of DSSA is: ', num2str(mean(Destination_fitness))]);
display(['The standard deviation fitness of DSSA is: ', num2str(std(Destination_fitness))]);
display(['The best location of DSSA is: ', num2str(bestPositions(index,:))]);

semilogy(Convergence_curve(index,:),'LineWidth',3);
xlabel('Iterations');
ylabel('Best fitness obtained so far');
legend('DSSA');
box on;
axis tight;
grid off;
%% Benchmark Test functions
function [lb,ub,dim,fobj] = Get_Functions_details(F)
switch F
    case 'F1'
        fobj = @F1;
        lb=-100;
        ub=100;
        dim=30;
        
    case 'F2'
        fobj = @F2;
        lb=-10;
        ub=10;
        dim=30;
        
    case 'F3'
        fobj = @F3;
        lb=-100;
        ub=100;
        dim=30;
        
    case 'F4'
        fobj = @F4;
        lb=-100;
        ub=100;
        dim=30;
        
    case 'F5'
        fobj = @F5;
        lb=-30;
        ub=30;
        dim=30;
        
    case 'F6'
        fobj = @F6;
        lb=-100;
        ub=100;
        dim=30;
        
    case 'F7'
        fobj = @F7;
        lb=-1.28;
        ub=1.28;
        dim=30;
        
    case 'F8'
        fobj = @F8;
        lb=-500;
        ub=500;
        dim=30;
        
    case 'F9'
        fobj = @F9;
        lb=-5.12;
        ub=5.12;
        dim=30;
        
    case 'F10'
        fobj = @F10;
        lb=-32;
        ub=32;
        dim=30;
        
    case 'F11'
        fobj = @F11;
        lb=-600;
        ub=600;
        dim=30;
        
    case 'F12'
        fobj = @F12;
        lb=-50;
        ub=50;
        dim=30;
        
    case 'F13'
        fobj = @F13;
        lb=-50;
        ub=50;
        dim=30;
        
    case 'F14'
        fobj = @F14;
        lb=-65.536;
        ub=65.536;
        dim=2;
        
    case 'F15'
        fobj = @F15;
        lb=-5;
        ub=5;
        dim=4;
        
    case 'F16'
        fobj = @F16;
        lb=-5;
        ub=5;
        dim=2;
        
    case 'F17'
        fobj = @F17;
        lb=[-5,0];
        ub=[10,15];
        dim=2;
        
    case 'F18'
        fobj = @F18;
        lb=-5;
        ub=5;
        dim=2;
        
    case 'F19'
        fobj = @F19;
        lb=0;
        ub=1;
        dim=3;
        
    case 'F20'
        fobj = @F20;
        lb=0;
        ub=1;
        dim=6;     
        
    case 'F21'
        fobj = @F21;
        lb=0;
        ub=10;
        dim=4;    
%         dim=4;
    case 'F22'
        fobj = @F22;
        lb=0;
        ub=10;
        dim=4;    
        
    case 'F23'
        fobj = @F23;
        lb=0;
        ub=10;
        dim=4;
    end
    
end

% F1

function o = F1(x)
o=sum(x.^2);
end

% F2

function o = F2(x)
o=sum(abs(x))+prod(abs(x));
end

  

 

  
 

四、运行结果

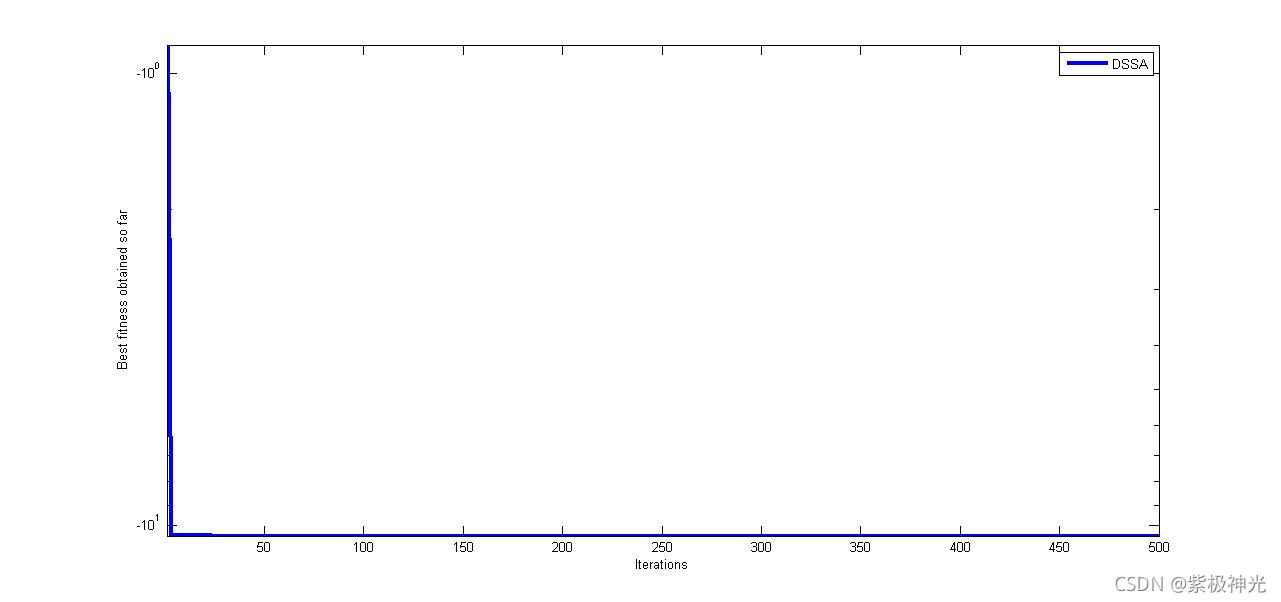
五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/120472169