【LSSVM分类】基于matlab灰狼算法优化LSSVM分类（多输入多分类）【含Matlab源码 1558期】

一、灰狼优化算法优化最小二乘支持向量机简介

1 灰狼优化算法
狼群具有严格的等级制度和明确的社会分工。S.Mirjalili等提出的灰狼优化算法是一种模拟狼群捕食行为的群体智能算法。其基本思想是将狼群中的狼依据捕食能力分为 α狼、β狼、δ狼和ω狼, 其中, α狼起带领作用, β狼和δ狼进行协助 (在本文中我们将这3种狼称为引导狼) , 而ω狼追随, 在优化的过程中, α狼始终是具有最优适应度的狼, 即最后的最优解。

在每次迭代过程中, 灰狼优化算法首先确定α狼、β狼和δ狼, 然后用引导狼去更新其余狼的位置信息, 其核心步骤可描述为

其中:i=1, 2, 3; Xi=α, β, δ;D表示当前狼个体与引导狼之间的距离;t为迭代次数;A为控制灰狼群体全局和局部搜索能力的因子;a为收敛因子, 其根据迭代次数t如 (5) 式线性减小 (其中的tmax为最大迭代次数) 。当|A|>1时, 灰狼群表现为较好的全局搜索能力;而当|A|<1时, 其表现为较好的局部搜索能力;r1和r2为[0, 1]之间的随机数。

在基本的GWO算法中, 收敛因子a线性递减, 并未考虑进化前后的差异, 理想情况应是在进化前期, a应具有变化较大的值, 以使A变化较快而具有更强的全局搜索能力;在后期a应具有变化较小的值, 以使A变化较慢而具有更强的局部搜索能力。除此之外, 在进行个体狼位置更新时, α狼、β狼和δ狼对个体的影响具有相同的权重, 忽视了引导狼的差异, 理想情况应是:越优的引导狼对个体狼的影响力越大。因此, 传统的GWO算法还有待改进。

2 最小二乘支持向量机
基于结构风险最小化原则和VC维理论, Vapnik等人提出了支持向量机SVM, 它是一种被广泛用于分类和回归的机器学习算法;而LSSVM是对SVM的改进, 其基本思想是采用非线性映射φ (x) 将训练样本从低维特征空间映射到高维特征空间中, 如此就把低维空间的非线性估计函数转化为高维空间的线性估计函数

输入训练样本{xi, yi}; i=1, 2, …, l。其中xi∈Rd是输入向量, 其维度为d;yi∈R是输出结果;l代表训练样本数;w、b分别是权值向量和偏置项;而φ (x) 为非线性映射函数。

LSSVM将误差平方和定义为损失函数, 将SVM的不等式约束二次规划问题变换为线性方程组的求解问题, 提高了收敛精度和求解速度。依据结构风险最小化原则, 求解 (7) 式最小的w和b的问题, 即求解式 (8) 表示的最优化问题

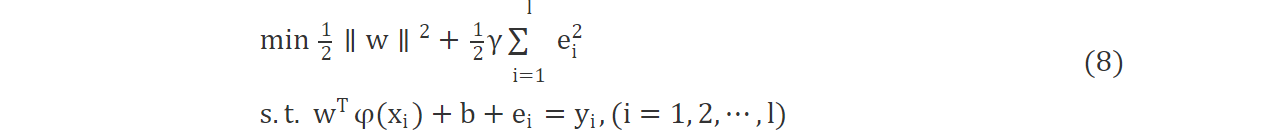
其中:γ为正规化参数;ei为松弛因子。为了求解式 (8) , 引入拉格朗日算子, 即可得到式 (9) 所示的非线性模型

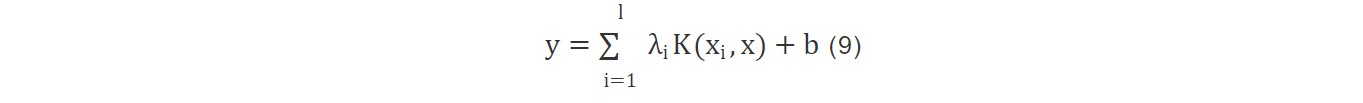
其中:λi∈Rl×1是拉格朗日乘子;K (·, ·) 是核函数, 其作用是把输入向量从低维空间映射到高维空间。几种常见的核函数如下:
多项式函数
K (x, xi) =[ (xi·x) +1]q (10)
RBF函数
K (x, xi) =exp (-‖x-xi‖2/2σ2) (11)
Sigmoid函数
K (x, xi) =tanh (ψ (x·xi) +c) (12)
以上这些核函数中, RBF是最常用的一种。本文所提出的信用评分模型中采用RBF核函数。
3 基于灰狼群优化算法的最小二乘支持向量机
基于灰狼群优化算法的最小二乘支持向量机 (IGWO-LSSVM) 采用灰狼群算法去优化LSSVM中的正则化参数[式 (8) 中γ]及RBF核中的宽度[式 (11) 中σ], 它们一起构成个体的2个维度, 即X=[γ σ]。为了评估个体X的好坏, 针对信用评估这个典型的分类问题, 以错分类比例作为适应度函数的值, 即

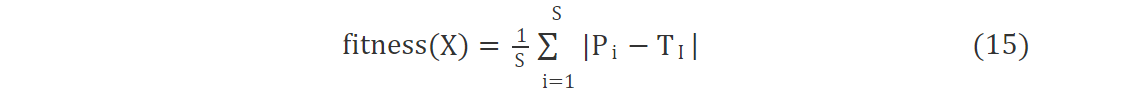
其中:S是测试集样本数;Pi和Ti分别是样本预测标签和实际标签。GWO-LSSVM的目标是最小化该适应度函数的值, 算法描述如下。
算法1: GWO-LSSVM
输入:N (灰狼群大小) ;tmax (最大进化代数) ;γmin、γmax (γ的最小值、最大值) ;σmin、σmax (σ的最小值、最大值) 。
输出:最优γ, σ。
步骤一:生成具有N个个体的初始种群, 每个个体是一个二维数据[γ σ];
步骤二:根据适应度函数 (15) 评价每个个体, 更新α狼、β狼和δ狼;
步骤三:根据公式 (13) 、 (14) 更新个体狼的收敛因子及位置信息;
步骤四:如果达到最大进化代数, 停止算法并输出最优值, 即α狼的位置。否则, 执行步骤二。
算法1的主要特点是能非线性调整收敛因子的值及根据引导狼的适应度值自适应地调整个体狼的位置信息。

二、部分源代码

 

  

 

  
1
 

三、运行结果

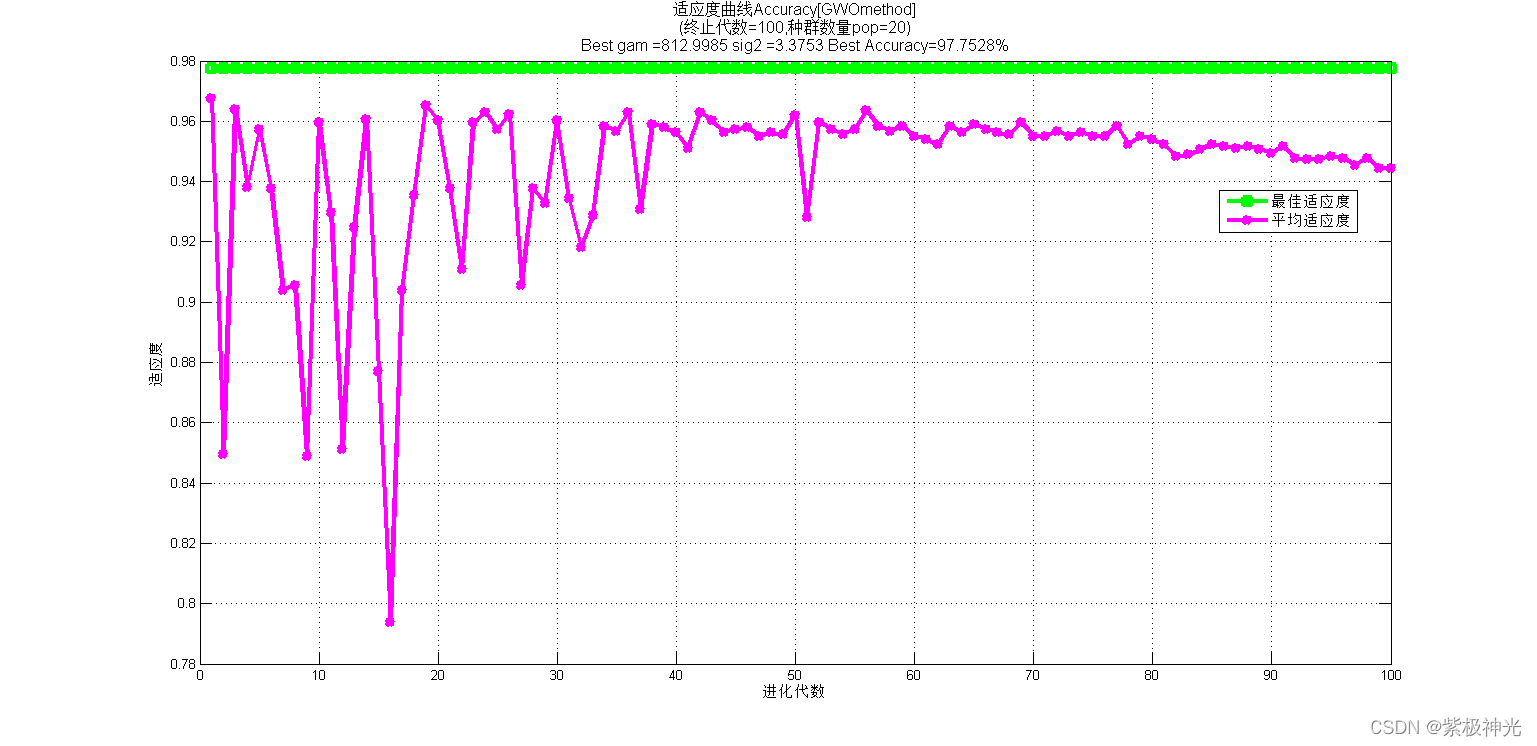
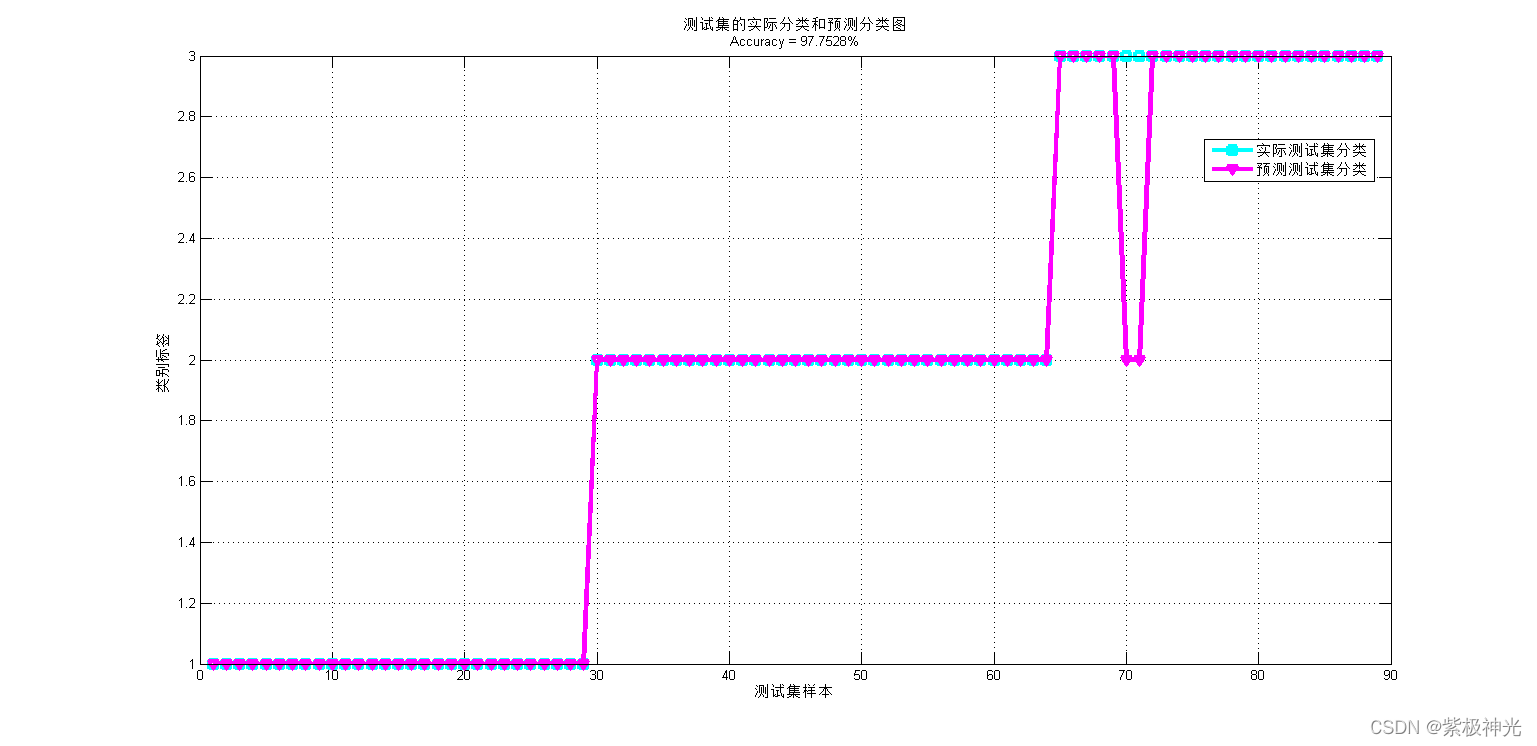
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.
[6]周敏.基于灰狼优化算法和最小二乘支持向量机的信用评估[J].成都理工大学学报(自然科学版). 2019,46(04)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/121611263