【单目标优化求解】基于matlab被囊群算法（TSA）求解最优目标问题【含Matlab源码 1567期】

一、获取代码方式

获取代码方式1：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

获取代码方式2：
完整代码已上传我的资源：[【单目标优化求解】基于matlab被囊群算法（TSA）求解最优目标问题【含Matlab源码 1567期】

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、被囊群算法简介

被囊群算法是一种元启发式算法，模拟被囊动物的喷气推进行为和群体行为.喷气推进行为主要利用自身的重力、深海中的水流平流、个体之间的相互作用力，实现个体之间搜索冲突避免，同时，也具有向最优个体移动的能力.喷气推进行为主要由3部分组成：搜索个体冲突避免，保持接近最佳搜索个体，向最佳个体的位置移动.群体行为主要为更新搜索个体最优解的位置，通过被囊动物周围的神经感知水流的变化和同伴的发光确定同伴位置，共同向目标食物源位置聚集，达到群体觅食的目的.TSA采用喷气推进行为和群体行为这两种策略，更真实地模拟海洋中被囊动物群体觅食行为，达到算法实现简单、跳出局部最优能力强、寻优精度高的目的.TSA具体流程如图1所示.

图1 TSA流程图
1 喷气推进行为
皮囊动物在进行喷气推进前，需要避免搜索个体之间的冲突.为了避免个体冲突，计算新的位置向量：
A=GM.
其中：G表示重力，计算方式由文献[15]给出；M表示搜索个体之间的社会力量，
M=⎣Pmin+c1(Pmax-Pmin)」,
Pmin、Pmax为社交活动的最小值和最大值，c1为[0,1]内的随机数.
在避免邻居之间的冲突后，搜索个体朝着最佳邻居的方向发展，此时需要计算搜索个体与食物源之间的距离.第t次迭代时第i个个体与食物来源之间的距离为
PDti=|positionstbest−rand⋅xti|,
其中，rand为满足[0,1]均匀分布的随机数，positionstbest为第t次迭代时种群食物来源位置，即当前种群最优个体位置，xti为第t次迭代时种群第i个皮囊个体位置.
搜索个体向最佳食物源位置移动，即

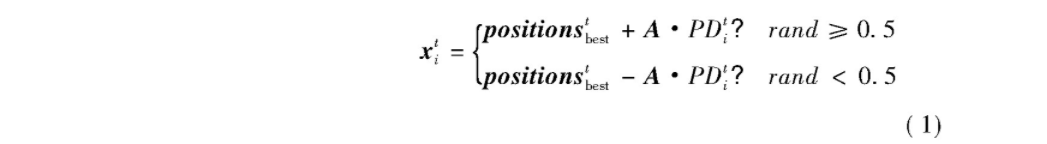
其中，positionstbest为第t次迭代时种群食物来源位置，A为个体避免冲突计算的位置向量，PDti为当前第i个个体与食物来源之间的距离.

2 群体行为
在避免冲突、计算个体与食物源位置距离后，皮囊个体采用群体行为向食物源聚集.为了从数学上模拟被囊动物的群体行为，定义被囊动物的群体行为：

三、部分源代码

%%%  Tunicate Swarm Algorithm (TSA)

clear all 
clc
SearchAgents=30; 
Fun_name='F1';  
Max_iterations=1000; 
[lowerbound,upperbound,dimension,fitness]=fun_info(Fun_name);
[Best_score,Best_pos,TSA_curve]=tsa(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness);


figure('Position',[300 300 660 290])

subplot(1,2,1);
func_plot(Fun_name);
title('Objective space')
xlabel('x_1');
ylabel('x_2');
zlabel([Fun_name,'( x_1 , x_2 )'])

subplot(1,2,2);
plots=semilogx(TSA_curve,'Color','g');
set(plots,'linewidth',2)
hold on
title('Objective space')
xlabel('Iterations');
ylabel('Best score');

axis tight
grid on
box on
legend('TSA')

display(['The best solution obtained by TSA is : ', num2str(Best_pos)]);
display(['The best optimal value of the objective funciton found by TSA is : ', num2str(Best_score)]);


%%% Designed and Developed by Dr. Gaurav Dhiman (http://dhimangaurav.com/) %%%

function func_plot(fun_name)

[lowerbound,upperbound,dimension,fitness]=fun_info(fun_name);

switch fun_name 
    case 'F1' 
        x=-100:2:100; y=x; %[-100,100]
        
    case 'F2' 
        x=-100:2:100; y=x; %[-10,10]
        
    case 'F3' 
        x=-100:2:100; y=x; %[-100,100]
        
    case 'F4' 
        x=-100:2:100; y=x; %[-100,100]
    case 'F5' 
        x=-200:2:200; y=x; %[-5,5]
    case 'F6' 
        x=-100:2:100; y=x; %[-100,100]
    case 'F7' 
        x=-1:0.03:1;  y=x  %[-1,1]
    case 'F8' 
        x=-500:10:500;y=x; %[-500,500]
    case 'F9' 
        x=-5:0.1:5;   y=x; %[-5,5]    
    case 'F10' 
        x=-20:0.5:20; y=x;%[-500,500]
    case 'F11' 
        x=-500:10:500; y=x;%[-0.5,0.5]
    case 'F12' 
        x=-10:0.1:10; y=x;%[-pi,pi]
    case 'F13' 
        x=-5:0.08:5; y=x;%[-3,1]
    case 'F14' 
        x=-100:2:100; y=x;%[-100,100]
    case 'F15' 
        x=-5:0.1:5; y=x;%[-5,5]
    case 'F16' 
        x=-1:0.01:1; y=x;%[-5,5]
    case 'F17' 
        x=-5:0.1:5; y=x;%[-5,5]
    case 'F18' 
        x=-5:0.06:5; y=x;%[-5,5]
    case 'F19' 
        x=-5:0.1:5; y=x;%[-5,5]
    case 'F20' 
        x=-5:0.1:5; y=x;%[-5,5]        
    case 'F21' 
        x=-5:0.1:5; y=x;%[-5,5]
    case 'F22' 
        x=-5:0.1:5; y=x;%[-5,5]     
    case 'F23' 
        x=-5:0.1:5; y=x;%[-5,5]  
end    

    

L=length(x);
f=[];

for i=1:L
    for j=1:L
        if strcmp(fun_name,'F15')==0 && strcmp(fun_name,'F19')==0 && strcmp(fun_name,'F20')==0 && strcmp(fun_name,'F21')==0 && strcmp(fun_name,'F22')==0 && strcmp(fun_name,'F23')==0
            f(i,j)=fitness([x(i),y(j)]);
        end
        if strcmp(fun_name,'F15')==1
            f(i,j)=fitness([x(i),y(j),0,0]);
        end
        if strcmp(fun_name,'F19')==1
            f(i,j)=fitness([x(i),y(j),0]);
        end
        if strcmp(fun_name,'F20')==1
            f(i,j)=fitness([x(i),y(j),0,0,0,0]);
        end       
        if strcmp(fun_name,'F21')==1 || strcmp(fun_name,'F22')==1 ||strcmp(fun_name,'F23')==1
            f(i,j)=fitness([x(i),y(j),0,0]);
        end          
    end
end

surfc(x,y,f,'LineStyle','none');

end


        

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
 

四、运行结果

五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]屈迟文,彭小宁1.信息共享的记忆被囊群算法[J].模式识别与人工智能. 2021,34(07)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/121777712