【优化算法】黑寡妇优化算法(BWOA)【含Matlab源码 1446期】
一、获取代码方式
获取代码方式1:
通过订阅紫极神光博客付费专栏,凭支付凭证,私信博主,可获得此代码。
获取代码方式2:
完整代码已上传我的资源:【优化算法】黑寡妇优化算法(BWOA)【含Matlab源码 1446期】
备注:
订阅紫极神光博客付费专栏,可免费获得1份代码(有效期为订阅日起,三天内有效);
二、黑寡妇优化算法简介
黑寡妇算法(Black Widow Optimization Algorithm, BWO)[2]是2020年由Vahideh Hayyolalam等人受黑寡妇蜘蛛独特的交配行为启发而提出的,该算法模拟了黑寡妇蜘蛛的生命周期,在51个基准函数以及3个具体工程问题上对BWO进行有效性验证,取得了良好的结果。
BWO的每一个解(潜在解决方案)是一只黑寡妇蜘蛛,黑寡妇蜘蛛的长度等于特征的维度。BWO包括初始化种群、生殖、同类相食、突变、更新种群等5个阶段,除了初始种群阶段,其他4个阶段需迭代至满足结束条件,返回适应度最佳的黑寡妇。
1 初始化种群
BWO中,待求解问题的一个解是一只黑寡妇蜘蛛,可以将黑寡妇蜘蛛视为一个一维数组:

其中,Nvar是特征的维度,初始化时,每个特征值都是随机的浮点数。每只黑寡妇都有适应度,使用某个适应度函数计算黑寡妇的适应度:
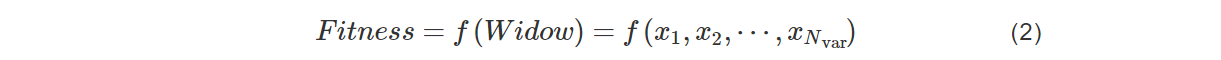
初始化种群时,需要生成Npop(种群大小)只黑寡妇,得到一个Npop×Nvar的黑寡妇矩阵。Npop需要预先定义,常用的有30、50等。
2 生殖
生殖阶段是全局搜索阶段。首先,根据适应度大小对种群排序,基于生殖率(procreating rate, PP)计算种群中参与生殖的黑寡妇,然后从中随机选择一对父母(雌雄黑寡妇)进行交配繁殖。在自然界中,每对黑寡妇都在自己的蜘蛛网上进行繁殖,与其他的黑寡妇是分开的,每次大约生成1000枚卵,但只有适应度较高的小蜘蛛能存活下来。在黑寡妇算法中,每对父母借助α数组模拟生殖过程:
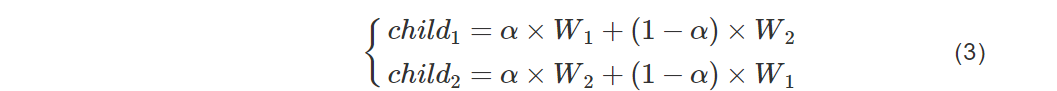
其中,W1和W2是父母,child1和child2是后代。这个过程要重复Nvar2次。
3 同类相食
同类相食指的是适应度高的蜘蛛吃掉适应度低的蜘蛛。黑寡妇蜘蛛的同类相食分为性同类相食、兄弟姐妹同类相食和子食母同类相食三种。性同类相食是指雌黑寡妇会在交配时或交配后吃掉雄黑寡妇,可以根据适应度分辨雌雄,适应度高的为雌性,适应度低的为雄性;兄弟姐妹同类相食发生在母蛛网上,幼蛛孵化后会在母蛛网上生活一周左右,期间会发生兄弟姐妹同类相食;子食母同类相食是指某些情况下会发生小蜘蛛吃掉母蛛的事件。黑寡妇算法中,模拟了性同类相食和兄弟姐妹同类相食,子食母同类相食暂未涉及。通过摧毁父亲实现性同类相食,根据同类相食率(cannibalism rate, CR)摧毁一部分孩子达到兄弟姐妹同类相食的目的。使用适应度值确定幼蛛的强弱。
4 突变
突变阶段是局部搜索阶段。黑寡妇算法在这一阶段根据突变率(mutation rate, PM)随机选择多个黑寡妇,每个黑寡妇随机交换数组中的两个特征值。
5 更新种群
一次迭代之后,将同类相食阶段保留下来的黑寡妇以及突变阶段得到的黑寡妇作为下一次迭代的初始种群。
6 停止条件
可以考虑三种停止条件:(1)提前设置最大迭代次数。(2)最佳黑寡妇不再发生变化。(3)达到预设的精度水平。
三、部分源代码
%_________________________________________________________________________%
% Black Widow Optimization Algorithm (source code) %
% %
% Developed in MATLAB R2018a(9.4) %
% %
% %
%_________________________________________________________________________%
clear
clc
SearchAgents_no=50; % number of Black Widows Spiders
Function_name='F1'; % <== write 'F2' or 'F3' and so on. Name of the test function that can be from F1 to F23, for F24+ are ing. problems.
Max_iteration=250; % Maximum numbef of iterations
[lb,ub,dim,fobj]=Get_Function(Function_name); % Load details of the selected benchmark function
[vMin,theBestVct,Convergence_curve]=BWOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
display(['The best solution obtained by BWOA is : ', num2str(theBestVct)]);
display(['The best optimal value of the objective funciton found by BWOA is : ', num2str(vMin)]);
%**********************************************************************************************************
_________________________________________________________________________%
% Benchmark functions
% lb is the lower bound: lb=[lb_1,lb_2,...,lb_d]
% up is the uppper bound: ub=[ub_1,ub_2,...,ub_d]
% dim is the number of variables (dimension of the problem)
%_________________________________________________________________________%
function [lb,ub,dim,fobj] = Get_Function(F)
switch F
case 'F1'
fobj = @F1;
lb=-100;
ub=100;
dim=30;
case 'F2'
fobj = @F2;
lb=-10;
ub=10;
dim=30;
case 'F3'
fobj = @F3;
lb=-100;
ub=100;
dim=30;
case 'F4'
fobj = @F4;
lb=-100;
ub=100;
dim=30;
case 'F5'
fobj = @F5;
lb=-30;
ub=30;
dim=30;
case 'F6'
fobj = @F6;
lb=-100;
ub=100;
dim=30;
case 'F7'
fobj = @F7;
lb=-1.28;
ub=1.28;
dim=30;
case 'F8'
fobj = @F8;
lb=-500;
ub=500;
dim=30;
case 'F9'
fobj = @F9;
lb=-5.12;
ub=5.12;
dim=30;
case 'F10'
fobj = @F10;
lb=-32;
ub=32;
dim=30;
case 'F11'
fobj = @F11;
lb=-600;
ub=600;
dim=30;
case 'F12'
fobj = @F12;
lb=-50;
ub=50;
dim=30;
case 'F13'
fobj = @F13;
lb=-50;
ub=50;
dim=30;
case 'F14'
fobj = @F14;
lb=-65.536;
ub=65.536;
dim=2;
case 'F15'
fobj = @F15;
lb=-5;
ub=5;
dim=4;
case 'F16'
fobj = @F16;
lb=-5;
ub=5;
dim=2;
case 'F17'
fobj = @F17;
lb=[-5,0];
ub=[10,15];
dim=2;
case 'F18'
fobj = @F18;
lb=-2;
ub=2;
dim=2;
case 'F19'
fobj = @F19;
lb=0;
ub=1;
dim=3;
case 'F20'
fobj = @F20;
lb=0;
ub=1;
dim=6;
case 'F21'
fobj = @F21;
lb=0;
ub=10;
dim=4;
case 'F22'
fobj = @F22;
lb=0;
ub=10;
dim=4;
case 'F23'
fobj = @F23;
lb=0;
ub=10;
dim=4;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
四、运行结果

五、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]李郅琴,杜建强,聂斌,熊旺平,徐国良,罗计根,李冰涛.基于黑寡妇算法的特征选择方法研究[J].计算机工程与应用
文章来源: qq912100926.blog.csdn.net,作者:海神之光,版权归原作者所有,如需转载,请联系作者。
原文链接:qq912100926.blog.csdn.net/article/details/120934692
- 点赞
- 收藏
- 关注作者


评论(0)