【图像加密】基于matlab RSA图像加密解密【含Matlab源码 1442期】

一、RSA图像加密简介

图像数据的获取、传输和处理已经遍及了数字时代的各个角落,图像的安全问题日益严重,尤其是在军事、商业和医疗等特殊领域 。RSA是一种目前被公开应用的加密算法,它采用非对称的加密体制 。下面,笔者在研究图像加密算法的基础上,将RSA算法应用到图像加密技术中,重点研究了算法优化、密钥生成、密钥分发和文件传输等内容,提出了一套完整的数字图像加密和解密解决方案。

1 RSA基本原理
RSA算法采用一种非对称密码加密体制,在整个加密过程中密钥和算法独立分开,使得密钥更能有效的等到分配 。其采用大素数因子分解的难度来保障安全性,目前,大素数分解问题仍然没有很好的解决方法 。
RSA算法加密的基本步骤如下:
Step1选取不同的2个大素数a,b,然后计算2个数乘积m=a×b。
Step2选取大整数加密密钥d,要求d与(a-1)×(b-1)互质。
Step3求解密密钥e,e×d=1mod(a-1)×(b-1)。
Step4将明文P加密为密文C(C=Pdmod m),密文C解密为明文P(P=Cemod m)。
根据以上步骤可以看出,只知道m和d不能计算出解密密钥e,可见,任何人都可以对明文P进行加密,但只有获得授权许可后才能对密文C进行解密。

2 RSA图像加密流程设计
RSA图像加密流程设计是先对图像进行读取并转化成十六进制数据流;然后生成RSA算法所需密钥,将密钥与图像进行幂乘及取模运算,生成十进制数据;最后将数据转换为字符串数据流进行保存。其中,最重要的是密钥的生成[ ,其决定最后图像加密效果。密钥的生成过程包括自动生成大素数并存储、对大素数进行算术运算、大数幂模与乘模运算和素数的自动生成4部分,具体加密流程如图1所示。

3 RSA图像加密功能设计
根据RSA图像加密流程,设计图像加密功能,主要包括RSA图像加密、解密和密钥生成等功能。系统功能模块如图2所示。
1)数字图像加密。对数字图像进行字节流的读取并转换为十六进制流,应用RSA算法对十六进制流进行加密,将加密后的数据转化为文本输出。
2)数字图像解密。加载加密后图像文件,利用密钥对其进行解密,对加密的图像进行还原。

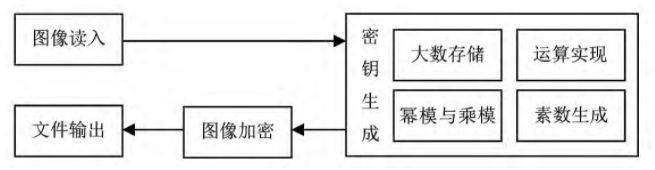
图1 RSA图像加密流程图

图2 系统功能模块图
3)加密解密预览。在数字图像加密解密过程中,确保待加密及解密后的数字图像可视化。
4)密钥自动生成。RSA算法需要用户自定义输入2个大素数,主要实现自动生成大素数及密钥以减少用户操作,并能确保密钥使用的素数足够大。
5)密钥长度设定。用户可根据不同情况设定密钥的长度,能够灵活控制加密和解密速度。
6)密钥文件导出。以文件形式导出密钥文件,确保传输或存储过程的安全性。
7)密钥文件导入。对导出的密钥文件进行读入,具有识别功能。可以识别本软件导出的密钥文件,并对内容检查,确保导入文件安全。
8)密钥输入。解密时支持手动输入加密处理的密钥串,确保解密操作安全。
9)文件打印。实现对密钥文件的打印,可以更好的保存私钥。
10)文件传输。实现加密后的文件及图像直接传输,方便快捷且能更好的确保安全。

4 RSA图像加密关键技术实现
4.1 RSA密钥的大数存储
RSA算法生成密钥需要2个大素数为21024或更大比较安全[7] 。但编程语言中unsigned int类型最多存储2个字节,远远小于RSA安全密钥长度。笔者设计单元线性数组实现大素数存储,解决编程中大素数的存储问题。首先设置一个以unsigned为单元的线性数组用来存储大素数,定义2个无符号整数z和n来控制存储单元数,z是分配空间的单元数,如果大素数的长度超过unsigned数组的预定义数组长度,z会随着数字变大不断增大;n表示当前存储大素数已占用单元数。每个大素数最大可以达到232*占用单元数满足RSA的各种运算。

4.2 RSA密钥的大数运算
由于生成的大素数超过21024,原有数据运算方式不再适用。在大数存储基础上采用类间派生与关联方式实现大数运算。定义flex_unit派生得到vlong_value类实现新的运算函数,将原vlong_value类关联到新类vlong中,在新vlong类实现运算符重载。本类运算是按一定数制对数字的计算,乘除和取余也都按照竖式运算的原理实现。加运算的核心代码如下:

4.3 大素数幂模与乘模运算优化
幂模运算是RSA算法中比重最大的计算,其主要决定生成最后的公钥和私钥,直接地决定了RSA算法的性能 。依据乘模的性质,把幂模运算转换成乘模运算,实现思想是指数不断的对分,具体流程如图3所示。

乘模运算能够提高运算速度,通常对于千位以上的二进制整数n,利用普通除法求模运算速度很慢[9] 。笔者采用Montgomery算法 实现幂乘运算的优化来提高加密速度,改进思想是先选取与模数m互素的基数Y(Y=2k),m为奇数满足2k-1≤m<2k,再选取Y-1(0<Y-1<m)和m′(0<m′<m),使得YY-1-mm′=1。然后选取任意整数n(0≤n<Ym),最后实现求模乘法nY-1mod m的快速算法,来提高加密运算速度。

4.4 算法中素数自动生成及优化
笔者采用Eratosthenes筛选法 对素数筛选进行优化,优化策略是对各小素数因子求模,得到当前a在素数搜索范围内的最小倍数在b[]中的对应位置,继续后移a个位置,直到将a在搜索范围内的所有倍数全部找到;在完成对所有小素数因子的类似操作后,其倍数在搜索范围内的位置标记b[r]被全部标记为0。其流程如图4所示。

图3 幂模转换乘模运算流程图

图4 素数搜索除去小素数因子倍数流程图
笔者采用费马小定理对素数测试进行优化,化策略是选取一个整数P,要求与a互素,并满足关系式为Pa-1mod a=1,输入大整数a满足关系式可能不是素数,需要改变P完成多次测试,测试后这个数很大概率为素数。

二、部分源代码

clc
clear all
close all

%% Initialization
Test=0; % for right key encryption
% Test=1; % for key sensitivity test
addpath functions
Images_Path='Images\Orignal\';
fname={'Lena','baboon','cameraman','panda','contact_lens','checkerboard','Black1','Onion','Football'}; % filename
ext='.jpg';
fid=1; % file ID 1 for lena
IS =256; % Image size
Data=imread(strcat(Images_Path,fname{fid},ext));
if (size(Data,3)==3)
    Data=rgb2gray(Data);
end
Data=imresize(Data,[IS IS]); % Image Size

[row,col]=size(Data);
[Data,padding]=Scalling(Data,8);
Data_binary=convert2bin(Data);

hex_key = 'AAAAAAAAAAAAAAAA';
[bin_key] = Hex2Bin( hex_key );
[K1,K2,K3,K4,K5]=SF_Key_Gen(bin_key);

orignal_msg=[];
encrypt_msg=[];
decrypt_msg=[];

%% Encryption Process
for kk=1:2
  for i=1:size(Data_binary,1)
    orignal=Data_binary(i,:);
    tic
    [cipher]=SF_Encrypt(orignal,K1,K2,K3,K4,K5);
    encryption_time(i)=toc;
    tK1=[K1(1:8),orignal(1:8)];tK2=orignal(9:24);tK3=orignal(25:40);tK4=orignal(41:56);tK5=[orignal(57:64),K5(9:16)];
    K1=tK1;K2=tK2;K3=tK3;K4=tK4;K5=tK5;
    
    encrypt_msg(:,i)=Binary2Dec(cipher);
    cipher_data(i,:)=double(cipher);
    if(kk<2)
    Data_binary(i,:)=cipher_data(i,:);
    end
  end
function O = P(I)
if(I==logical([0 0 0 0]))
        O = logical([0 0 1 1]); end
if(I==logical([0 0 0 1]))
        O = logical([1 1 1 1]); end
if(I==logical([0 0 1 0]))
        O = logical([1 1 1 0]); end
if(I==logical([0 0 1 1]))
        O = logical([0 0 0 0]); end
if(I==logical([0 1 0 0]))
        O = logical([0 1 0 1]); end
if(I==logical([0 1 0 1]))
        O = logical([0 1 0 0]); end
if(I==logical([0 1 1 0]))
        O = logical([1 0 1 1]); end  
if(I==logical([0 1 1 1]))
        O = logical([1 1 0 0]); end  
if(I==logical([1 0 0 0]))
        O = logical([1 1 0 1]); end  
if(I==logical([1 0 0 1]))
        O = logical([1 0 1 0]); end
if(I==logical([1 0 1 0]))
        O = logical([1 0 0 1]); end  
if(I==logical([1 0 1 1]))
        O = logical([0 1 1 0]); end   
if(I==logical([1 1 0 0]))
        O = logical([0 1 1 1]); end  
if(I==logical([1 1 0 1]))
        O = logical([1 0 0 0]); end  
if(I==logical([1 1 1 0]))
        O = logical([0 0 1 0]); end  
if(I==logical([1 1 1 1]))
        O = logical([0 0 0 1]); end  
end
function O = Q(I)
if(I==logical([0 0 0 0]))
        O = logical([1 0 0 1]); end
if(I==logical([0 0 0 1]))
        O = logical([1 1 1 0]); end
if(I==logical([0 0 1 0]))
        O = logical([0 1 0 1]); end
if(I==logical([0 0 1 1]))
        O = logical([0 1 1 0]); end
if(I==logical([0 1 0 0]))
        O = logical([1 0 1 0]); end
if(I==logical([0 1 0 1]))
        O = logical([0 0 1 0]); end
if(I==logical([0 1 1 0]))
        O = logical([0 0 1 1]); end
if(I==logical([0 1 1 1]))
        O = logical([1 1 0 0]); end
if(I==logical([1 0 0 0]))
        O = logical([1 1 1 1]); end
if(I==logical([1 0 0 1]))
        O = logical([0 0 0 0]); end
if(I==logical([1 0 1 0]))
        O = logical([0 1 0 0]); end
if(I==logical([1 0 1 1]))
        O = logical([1 1 0 1]); end
if(I==logical([1 1 0 0]))
        O = logical([0 1 1 1]); end
if(I==logical([1 1 0 1]))
        O = logical([1 0 1 1]); end
if(I==logical([1 1 1 0]))
        O = logical([0 0 0 1]); end
if(I==logical([1 1 1 1]))
        O = logical([1 0 0 0]); end
end

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
 

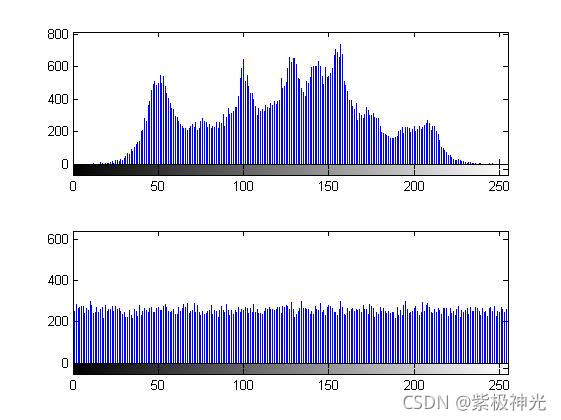
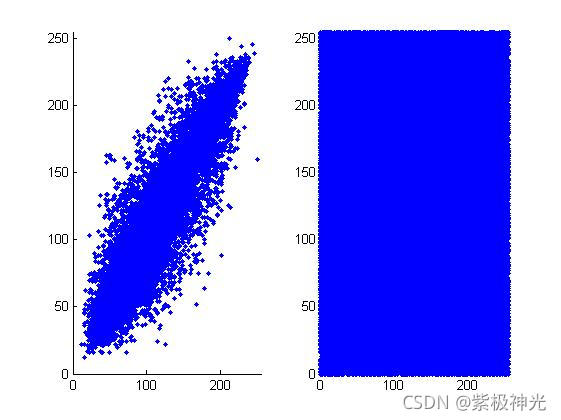
三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 蔡利梅.MATLAB图像处理——理论、算法与实例分析[M].清华大学出版社，2020.
[2]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社，2013.
[3]周品.MATLAB图像处理与图形用户界面设计[M].清华大学出版社，2013.
[4]刘成龙.精通MATLAB图像处理[M].清华大学出版社，2015.
[5]高新成,王莉利,李苏龙.基于RSA算法的图像加密系统设计与实现[J].长江大学学报(自科版). 2016,13(25)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/120977746