【优化算法】多目标萤火虫算法（MOFA）【含Matlab源码 1595期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【优化算法】多目标萤火虫算法（MOFA）【含Matlab源码 1595期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、萤火虫优化算法（FA）简介

1 介绍
萤火虫（firefly）种类繁多，主要分布在热带地区。大多数萤火虫在短时间内产生有节奏的闪光。这种闪光是由于生物发光的一种化学反应，萤火虫的闪光模式因种类而异。萤火虫算法(FA)是基于萤火虫的闪光行为，它是一种用于全局优化问题的智能随机算法，由Yang Xin-She（2009）[1]提出。萤火虫通过下腹的一种化学反应-生物发（bioluminescence）发光。这种生物发光是萤火虫求偶仪式的重要组成部分，也是雄性萤火虫和雌性萤火虫交流的主要媒介，发出光也可用来引诱配偶或猎物，同时这种闪光也有助于保护萤火虫的领地，并警告捕食者远离栖息地。在FA中，认为所有的萤火虫都是雌雄同体的，无论性别如何，它们都互相吸引。该算法的建立基于两个关键的概念：发出的光的强度和两个萤火虫之间产生的吸引力的程度。

2 天然萤火虫的行为
天然萤火虫在寻找猎物、吸引配偶和保护领地时表现出惊人的闪光行为，萤火虫大多生活在热带环境中。一般来说，它们产生冷光，如绿色、黄色或淡红色。萤火虫的吸引力取决于它的光照强度，对于任何一对萤火虫来说，较亮的萤火虫会吸引另一只萤火虫。所以，亮度较低的个体移向较亮的个体，同时光的亮度随着距离的增加而降低。萤火虫的闪光模式可能因物种而异，在一些萤火虫物种中，雌性会利用这种现象猎食其他物种；有些萤火虫在一大群萤火虫中表现出同步闪光的行为来吸引猎物，雌萤火虫从静止的位置观察雄萤火虫发出的闪光，在发现一个感兴趣趣的闪光后，雌性萤火虫会做出反应，发出闪光，求偶仪式就这样开始了。一些雌性萤火虫会产生其他种类萤火虫的闪光模式，来诱捕雄性萤火虫并吃掉它们。

3 萤火虫算法
萤火虫算法模拟了萤火虫的自然现象。真实的萤火虫自然地呈现出一种离散的闪烁模式，而萤火虫算法假设它们总是在发光。为了模拟萤火虫的这种闪烁行为，Yang Xin-She提出了了三条规则（Yang，2009）：
（1）假设所有萤火虫都是雌雄同体的，因此一只萤火虫可能会被其他任何萤火虫吸引。
（2）萤火虫的亮度决定其吸引力的大小，较亮的萤火虫吸引较暗的萤火虫。如果没有萤火虫比被考虑的萤火虫更亮，它就会随机移动。
（3）函数的最优值与萤火虫的亮度成正比。
光强(I)与光源距离（r）服从平方反比定律，因此由于空气的吸收，光的强度(I)随着与光源距离的增加而减小，这种现象将萤火虫的可见性限定在了非常有限的半径内：

萤火虫算法的主要实现步骤如下：

其中I0为距离r=0时的光强（最亮），即自身亮度，与目标函数值有关，目标值越优，亮度越亮；γ为吸收系数，因为荧光会随着距离的增加和传播媒介的吸收逐渐减弱，所以设置光强吸收系数以体现此特性，可设置为常数；r表示两个萤火虫之间的距离。有时也使用单调递减函数，如下式所示。

第二步为种群初始化：

其中t表示代数，xt表示个体的当前位置，β0exp(-γr2)是吸引度，αε是随机项。下一步将会计算萤火虫之间的吸引度：

其中β0表示r=0时的最大吸引度。
下一步，低亮度萤火虫向较亮萤火虫运动：

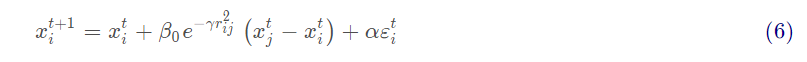
最后一个阶段，更新光照强度，并对所有萤火虫进行排序，以确定当前的最佳解决方案。萤火虫算法的主要步骤如下所示。

Begin
	初始化算法基本参数：设置萤火虫数目n，最大吸引度β0，光强吸收系数γ，步长因子α，最大迭代次数MaxGeneration或搜索精度ε；
	初始化：随机初始化萤火虫的位置，计算萤火虫的目标函数值作为各自最大荧光亮度I0；
	t=1
	while(t<=MaxGeneration || 精度>ε)
		计算群体中萤火虫的相对亮度I(式2)和吸引度β（式5），根据相对亮度决定萤火虫的移动方向；
		更新萤火虫的空间位置，对处在最佳位置的萤火虫进行随机移动（式6）；
		根据更新后萤火虫的位置，重新计算萤火虫的亮度I0；
		t=t+1
	end while
	输出全局极值点和最优个体值。
end


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
 

萤火虫算法与粒子群算法(PSO)和细菌觅食算法(BFA)有相似之处。在位置更新方程中，FA和PSO都有两个主要分量：一个是确定性的，另一个是随机性的。在FA中，吸引力由两个组成部分决定：目标函数和距离，而在BFA中，细菌之间的吸引力也有两个组成部分：适应度和距离。萤火虫算法实现时，整个种群(如n)需要两个内循环，特定迭代需要一个外循环(如I)，因此最坏情况下FA的计算复杂度为O(n2I)。

三、部分源代码

%% This demo shows how the multiobjective firefly algorithm (MOFA) works  %
%%
% -----------------------------------------------------------------------

function mofa_new(inp)  
if nargin<1,    
  inp=[100 1000]; % Default parameters
end
n=inp(1);               % Population size (number of fireflies)
tMax=inp(2);            % Maximum number of iterations
alpha=1.0;              % Randomness strength 0--1 (highly random)
beta0=1.0;              % Attractiveness constant
gamma=0.1;              % Absorption coefficient
theta=10^(-4/tMax);     % The parameter theta can be taken as 0.97 to 0.99    
                        % This is a randomness reduction factor for alpha

% For the ZDT Function #3 with m=2 objectives
m=2;             % Number of objectives
RnD=zeros(n,2);  % Initilize the rank and distance matrix
% Dimension of the search/independent variables
d=30;
Lb=0*ones(1,d);   % Lower bounds/limits
Ub=1*ones(1,d);   % Upper bounds/limits
% Generating the initial locations of n fireflies
for i=1:n,
   Sol(i,:)=Lb+(Ub-Lb).*rand(1,d); 
   f(i,1:m) = obj_funs(Sol(i,:), m);
end
% Store the fitness or objective values
f_new=f;
%% Sort the initialized population
x=[Sol f];  % combined into a single input
% Non-dominated sorting for the initila population
Sorted=solutions_sorting(x, m,d);
% Decompose into solutions, fitness, rank and distances
Sol=Sorted(:,1:d);  S_new=Sol;       % Record solutions 
f=Sorted(:,(d+1):(d+m));  f_new=f;   % Record objectives
RnD=Sorted(:,(d+m+1):end);           % Record ranks
   
for t=1:tMax,          %%%%% start the firely algorithm iterations %%%%%
   alpha=alpha*theta;  % Reduce alpha by a factor 0<theta<1
   scale=abs(Ub-Lb);   % Scale of the optimization problem
   Sol_old=Sol;        % Save the old population
   f_old=f;            % Save the old population objectives
% Two loops over all the n fireflies
for i=1:n,
    for j=i:n, 
      % Update moves and move to the brighter/more attractive
      % That is, all m objectives [i.e., f(,1:m)] should improve. 
      % For example, for m=2, this means that the logical 
      % condition (f(j,1)<=f(i,1) & f(j,2) <=f(i,2)) is true.     
      if (f(j,1:m)<=f(i,1:m)),     
         r=sqrt(sum((Sol(i,:)-Sol(j,:)).^2));
         beta=beta0*exp(-gamma*r.^2);     % Attractiveness
         steps=alpha.*(rand(1,d)-0.5).*scale;
      % The FA equation for updating position vectors 
      % That is, to move firefly i torwards firefly j
         Sol(i,:)=Sol(i,:)+beta*(Sol(j,:)-Sol(i,:))+steps;
         Sol(i,:)=simplebounds(Sol(i,:),Lb,Ub);
      end
         f(i,1:m)=obj_funs(Sol(i,1:d),m);   
   end % end for j
end % end for i
   
   %% Evalute the fitness/function values of the new population
   for j=1:n,
        f_new(j, 1:m)=obj_funs(Sol(j,1:d),m);
        if (f_new(j,1:m) <= f(j,1:m)),   % if all improve
            f(j,1:m)=f_new(j,1:m);
        end
        % Update the current best (stored in the first row)
        if (f_new(j,1:m) <= f(1,1:m)), 
            Sol(1,1:d) = Sol(j,1:d); 
            f_new(1,:)=f_new(j,:);
        end
     end % end of for loop j
     
%% ! It's very important to combine both populations, otherwise,
%% the results may look odd and will be very inefficient. !     
%% The combined population consits of both the old and new solutions
%% So the total size of the combined population for sorting is 2*n
       X(1:n,:)=[Sol f_new];               % Combine new solutions
       X((n+1):(2*n),:)=[Sol_old f_old];   % Combine old solutions
       Sorted=solutions_sorting(X, m, d);
       %% Select n solutions among a combined population of 2*n solutions
       new_Sol=Select_pop(Sorted, m, d, n);
       % Decompose into solutions, fitness and ranking
       Sol=new_Sol(:,1:d);             % Sorted solutions
       f=new_Sol(:,(d+1):(d+m));       % Sorted objective values
       RnD=new_Sol(:,(d+m+1):end);     % Sorted ranks and distances
    
  %% Running display at each 100 iterations
   if ~mod(t,100), 
     disp(strcat('Iterations t=',num2str(t))); 
     plot(f(:, 1), f(:, 2),'ro','MarkerSize',3); 
     axis([0 1 -0.8 1]);
     xlabel('f_1'); ylabel('f_2');
     drawnow;
   end        

end % End of t loop (up to tMax) and end of the main FA loop  

%% Make sure that new fireflies are within the bounds/limits
function s=simplebounds(s,Lb,Ub)
  % Apply the lower bound
  ns_tmp=s;
  I=ns_tmp<Lb;
  ns_tmp(I)=Lb(I);
  % Apply the upper bounds 
  J=ns_tmp>Ub;
  ns_tmp(J)=Ub(J);
  % Update this new move 
  s=ns_tmp;
  
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Objective functions
function f = obj_funs(x, m)
% Zitzler-Deb-Thiele's funciton No 3 (ZDT function 3)
% m = # of objectives   % d = # of variables/dimensions
d=length(x);  % d=30 for ZDT 3
% First objective f1
f(1) = x(1);
g=1+9/29*sum(x(2:d));

%%%%%%%%%%%%%%%%%% end of the definitions of obojectives %%%%%%%%%%%%%%%%%%

function new_Sol = Select_pop(firefly, m, ndim, npop)
% The input population to this part has twice (ntwice) of the needed 
% population size (npop). Thus, selection is done based on ranking and 
% crowding distances, calculated from the non-dominated sorting
ntwice= size(firefly,1);
% Ranking is stored in column Krank
Krank=m+ndim+1;
% Sort the population of size 2*npop according to their ranks
[~,Index] = sort(firefly(:,Krank)); 
sorted_firefly=firefly(Index,:);
% Get the maximum rank among the population
RankMax=max(firefly(:,Krank)); 

%% Main loop for selecting solutions based on ranks and crowding distances

for i =1:RankMax,  
    % Obtain the current rank i from sorted solutions
    RankSol = max(find(sorted_firefly(:, Krank) == i));
    % In the new solutions, there can be npop solutions to fill
    if RankSol<npop,
       new_Sol(K+1:RankSol,:)=sorted_firefly(K+1:RankSol,:);
    end 
    % If the population after addition is large than npop, re-arrangement
    % or selection is carried out
    if RankSol>=npop
        % Sort/Select the solutions with the current rank 
        candidate_firefly=sorted_firefly(K + 1 : RankSol, :);
        [~,tmp_Rank]=sort(candidate_firefly(:,Krank+1),'descend');
        % Fill the rest (npop-K) fireflies/solutions up to npop solutions 
        for j = 1:(npop-K), 
            new_Sol(K+j,:)=candidate_firefly(tmp_Rank(j),:);
        end
    end
    % Record and update the current rank after adding new solutions
    K = RankSol;
end



  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
  
144
  
145
  
146
  
147
  
148
  
149
  
150
  
151
  
152
  
153
  
154
  
155
  
156
  
157
  
158
  
159
  
160
  
161
  
162
  
163
  
164
 

四、运行结果

五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]群体智能优化算法之萤火虫算法(Firefly Algorithm，FA)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/121894793