【优化算法】非支配排序遗传算法（NSGA）【含Matlab源码 176期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【优化算法】非支配排序遗传算法（NSGA）【含Matlab源码 176期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、遗传算法简介

非支配排序遗传算法NSGA(Non-dominated So rng Genetic Algor thms) 是由Srinivas和Deb于1995年提出的”。这是一种基于Pareto最优概念的遗传算法， 它是众多的多目标优化遗传算法中体现God beg思想最直接的方法。该算法就是在基本遗传算法的基础上，对选择再生方法进行改进：将每个个体按照它们的支配与非支配关系进行分层，再做选择操作，从而使得该算法在多目标优化方面得到非常满意的结果。Z it z ler与Thiele等191曾对NSGA、NPG A、VEGA， 与Haj ela和Lin的加权向量算法以及纯随机搜索算法，作了系统的定量实验比较。通过采用多背包问题扩展形式的九种不同规模设置作为数值型多目标测试问题，经过全面的比较分析， 得到比较结果：NSGA的性能最优， 其次是VEGA， 而NPG A与Haj ela和Lin的加权向量算法的全部实验结果不分上下例。虽然这种比较结果不能无限制
的外推， 但是它在一定程度上说明了NSGA具有一定的优越性。因此， 对该算法进行理论研究和应用研究具有十分重要的意义。

虽然NSGA与其它多目标优化遗传算法比较具有一定的优越性：优化目标个数任选，非劣最优解分布均匀，并允许存在多个不同的等价解。但它仍存在一些问题(例：a)计算复杂度较高，当种群较大时，计算相当耗时；b)没有精英策略，精英策略可以加速算法的执行速度，而且也能在一定程度上确保已经找到的满意解不被丢失； c) 需要指定共享半径o， hare·

三、部分源代码

function NSGAII()
clc;
% format compact;
tic;
% hold on

%--初始化 参数设定
generations=100;        %迭代次数
popnum=100;             %种群大小（偶数）
poplength=30;           %个体长度
minvalue=repmat(zeros(1,poplength),popnum,1);   %个体最小值---B = repmat(A, m, n) %将矩阵A复制m*n块，即B由m*n块A平铺而成
maxvalue=repmat(ones(1,poplength),popnum,1);    %个体最大值
population=rand(popnum,poplength).*(maxvalue-minvalue)+minvalue;    %产生新的初始种群

    %--开始迭代进化
    for gene=1:generations      %开始迭代

        %--交叉
        newpopulation=zeros(popnum,poplength);  %子代种群
        for i=1:popnum/2                        %交叉产生子代
            k=randperm(popnum);                 %从种群中随机选择出两个父母，不采用二进制联赛方法
            beta=(-1).^round(rand(1,poplength)).*abs(randn(1,poplength))*1.481;     %采用正态分布交叉产生两个子代
            newpopulation(i*2-1,:)=(population(k(1),:)+population(k(2),:))/2+beta.*(population(k(1),:)-population(k(2),:))./2;  %产生第一个子代
            newpopulation(i*2,:)=(population(k(1),:)+population(k(2),:))/2-beta.*(population(k(1),:)-population(k(2),:))./2;    %产生第二个子代
        end
        %--变异
       
        newpopulation(temp)=newpopulation(temp)+(maxvalue(temp)-minvalue(temp)).*((2.*miu(temp)+(1-2.*miu(temp)).*(1-(newpopulation(temp)-minvalue(temp))./(maxvalue(temp)-minvalue(temp))).^21).^(1/21)-1);        %变异情况一
        newpopulation(temp)=newpopulation(temp)+(maxvalue(temp)-minvalue(temp)).*(1-(2.*(1-miu(temp))+2.*(miu(temp)-0.5).*(1-(maxvalue(temp)-newpopulation(temp))./(maxvalue(temp)-minvalue(temp))).^21).^(1/21));  %变异情况二

        %--越界处理/种群合并
        newpopulation(newpopulation>maxvalue)=maxvalue(newpopulation>maxvalue); %子代越上界处理
        newpopulation(newpopulation<minvalue)=minvalue(newpopulation<minvalue); %子代越下界处理
      

        %--计算目标函数值
        functionvalue=zeros(size(newpopulation,1),2);   %合并后种群的各目标函数值，这里问题是ZDT1
        functionvalue(:,1)=newpopulation(:,1);   %计算第一维目标函数值
        g=1+9*sum(newpopulation(:,2:poplength),2)./(poplength-1);
        functionvalue(:,2)=g.*(1-(newpopulation(:,1)./g).^0.5); %计算第二维目标函数值

        %--非支配排序
        fnum=0;     %当前分配的前沿面编号
        cz=false(1,size(functionvalue,1));      %记录个体是否已被分配编号
        frontvalue=zeros(size(cz));             %每个个体的前沿面编号
        [functionvalue_sorted,newsite]=sortrows(functionvalue); %对种群按第一维目标值大小进行排序 则第一行个体p即为种群中支配个体p的数量为零的个体，Np=0
        while ~all(cz)      %开始迭代判断每个个体的前沿面，采用改进的deductive sort
            fnum=fnum+1;
            d=cz;
            
                if ~d(i)
                    for j=i+1:size(functionvalue,1) %判断i对应的所有集合里面的支配和非支配的解，被i支配则为1，不被i支配则为0
                        if ~d(j)
                            k=1;
                            for m=2:size(functionvalue,2) %判断是否支配，找到个体p不支配的个体，标记为k=0
                                if functionvalue_sorted(i,m)>functionvalue_sorted(j,m) %判断i,j是否支配，如果成立i,j互不支配
                                    k=0; %i,j互不支配
                                    break;
                                end
                            end
                            if k
                                d(j)=true;  %那么p所支配的个体k=1并记录在d里，则后面该个体已被支配就不能在这一层里进行判断
                            end
                        end
                    end
                    frontvalue(newsite(i))=fnum; %实际位置的非支配层赋值
                    cz(i)=true;
                end
            end
        end

        %--计算拥挤距离/选择出下一代个体
       
        popu=find(frontvalue==fnum+1);   %popu记录第fnum+1个面上的个体编号
        distancevalue=zeros(size(popu));    %popu各个体的拥挤距离
        fmax=max(functionvalue(popu,:),[],1);   %popu每维上的最大值
        fmin=min(functionvalue(popu,:),[],1);   %popu每维上的最小值
        for i=1:size(functionvalue,2)   %分目标计算每个目标上popu各个体的拥挤距离
            [~,newsite]=sortrows(functionvalue(popu,i)); %popu里对第一维排序之后的位置
            distancevalue(newsite(1))=inf;
            distancevalue(newsite(end))=inf;
            for j=2:length(popu)-1
                distancevalue(newsite(j))=distancevalue(newsite(j))+(functionvalue(popu(newsite(j+1)),i)-functionvalue(popu(newsite(j-1)),i))/(fmax(i)-fmin(i)); %
            end
        end
        popu=-sortrows(-[distancevalue;popu]')';    %按拥挤距离降序排序第fnum+1个面上的个体
        population(newnum+1:popnum,:)=newpopulation(popu(2,1:popnum-newnum),:); %将第fnum+1个面上拥挤距离较大的前popnum-newnum个个体复制入下一代
    end

%--程序输出
fprintf('已完成，耗时%4s秒\n',num2str(toc));    %程序最终耗时
output=sortrows(functionvalue(frontvalue==1,:));    %最终结果：种群中非支配解的函数值
plot(output(:,1),output(:,2),'*b');             %作图
axis([0,1,0,1]);
xlabel('F_1');
ylabel('F_2');
title('ZDT1');


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
 

四、运行结果

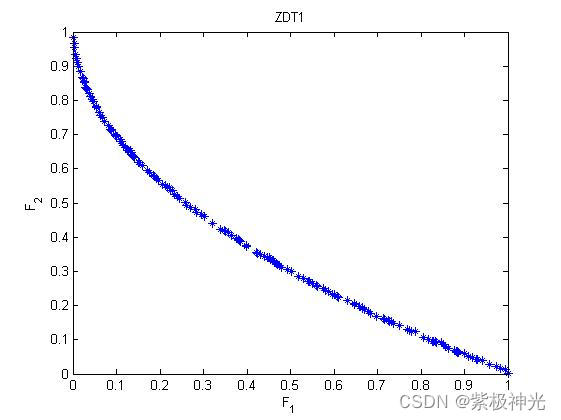
五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]包子阳 ,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[J].电子工业出版社
[2]高媛.非支配排序遗传算法（NSGA）的研究与应用[D].浙江大学

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/122016824