【优化覆盖】基于matlab粒子群算法求解传感器覆盖优化问题【含Matlab源码 1493期】

一、无线传感器网络覆盖优化问题简介

1无线传感器网络覆盖优化问题
1.1 无线传感器网络模型
在无线传感器网络中, 节点数量以及节点划分区域直接关系着无线传感器网络对目标事物覆盖死角面积, 增多节点数量能够提高网络覆盖密度。将节点更多地划分在离目标事物距离近的区域内, 可以增强网络数据传输的安全性和准确性。无线传感器网络认知模型搭建的目的就是对无线传感器网络的覆盖死角进行定义和测量, 为此, 基于粒子群算法的无线传感器网络覆盖优化方法可看成是对认知模型的参数优化问题。

传感器网络节点容易受到噪音和电磁波的扰乱造成传输误差, 这些因不可抗拒因素导致的一系列缩减网络覆盖率问题被统称为无效事件。设无线传感器网络认知模型在起点坐标为S、终点坐标为p的节点上测量到存在无效事件的几率为P (S, p) , 降低P (S, p) 即可提高覆盖率。P (S, p) 的定义式为:

式中:β是节点认知力衰减函数;d (S, p) 表示S与p之间的欧几里得度量。

从式 (1) 中能够明显看出, 如果d (S, p) =0, 则P (S, p) =1, 此时的模型测量工作是无意义的。为此, 需要对式 (1) 进行改进, 为其指定一个节点几率约束值r, 则式 (1) 可变更为:

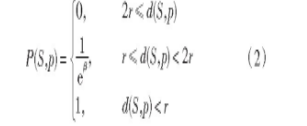
式 (2) 可表示无线传感器网络认知模型的最终表达式, 从中能够得知, 模型已将无线传感器网络覆盖优化工作转化成在r≤d (S, p) <2r条件下的P (S, p) 最小值问题。

1.2 覆盖率优化问题描述
将无线传感器网络对目标物体的监控区域看成一个二维区域, 二维区域中存在N个已知坐标的节点, 设区域中所有节点的认知半径均为R1, 节点传输半径均为R2。若想在维系网络稳定通信的同时将电磁波的不良影响降至最低, 可令R2=2R1。

式中:β1, β2是无线传感器网络节点的测量项目数据;λ1, λ2是参数, λ1=r+d, λ2=2r-d。

将式 (3) 耦合可以得到无线传感器网络覆盖率的表达式:

2 粒子群算法的传感器网络覆盖优化
根据上述描述, 使用粒子群算法优化无线传感器网络覆盖率, 简要介绍粒子群算法的基本原理, 对网络覆盖优化流程进行重点设计。

2.1 粒子群算法的工作原理
粒子群算法是进化算法的一个流派, 也是生物随机索引算法中的一个分支, 是当前的研究热点。粒子群算法的基本原理如图1所示。

图1 粒子群算法基本原理
由图1可知, 粒子群算法的实现非常简单, 其基本原理就是使用迭代方式得到最优解, 对粒子的速度和坐标进行实时更新。算法先初始化粒子, 将历史最优解赋予粒子。在算法进入迭代流程前, 先设置一个位置参数g的最大值, 即循环系数, 负责控制算法的迭代次数。每迭代一次, 位置参数g的值便增加1, 当g大于循环系数, 则停止迭代。粒子群算法的迭代工作可得到粒子适应度, 并以适应度为标准依次更新粒子的历史最优解、粒子群最优解以及粒子的速度和坐标。粒子速度vN1与坐标xi1的更新方程为:

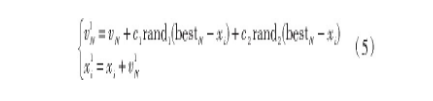
式中:vN, xi是粒子初始设定值;c1, c2是粒子群算法的学习因子, 通常取值为2;rand1, rand2是随机参数;bestN是粒子适应度约束值。

2.2 无线传感器网络覆盖优化流程
基于粒子群算法的无线传感器网络覆盖优化方法的优化流程如图2所示。

图2 无线传感器网络覆盖优化流程
首先对模型进行编码, 其目的是固定节点位置, 粒子群算法的编码是一种二进制百兆数据码, 编码长度与无线传感器网络节点数量相等。当模型中节点参数满足r≤d<2r, 为获取P (x, y, cN) 的最大值, 粒子群算法的编码结果应满足下式:

式 (6) 中的元素取值为0或1, 0表示传感器节点可以被重新安置, 1表示固定节点。

适应度是评价最优解质量的函数, 在粒子群算法进行迭代工作前, 需要提前设置适应度函数并计算出无线传感器网络认知模型的初始适应度, 方便对迭代结果进行对比, 输出最合适的节点优化位置, 实现对无线传感器网络覆盖率的最佳优化。

在式 (6) 给出的编码基础上, 使用式 (7) 计算模型适应度:

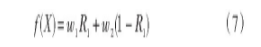
式中:无线传感器网络覆盖率瞬时值R1可通过式 (4) 进行求取;w1和w2分别表示R1在无线传感器网络中的初始权重和实际权重。

当式 (7) 满足w1+w2=1时, P (x, y, cN) 可达最大值。因此, 粒子群算法迭代工作的目标就是令w1+w2=1。实现迭代目标后, 基于粒子群算法的无线传感器网络覆盖优化方法需要对无线传感器网络的节点位置进行更新, 并输出优化后的无线传感器网络覆盖率。

二、部分源代码

%*****************粒子群算法实现**********************
%%
clc
clear
clear all
%%
%设定通信半径为12
tic;

R=12;
%% 粒子群参数
maxgen=1000;               %迭代次数
sizepop=30;               %粒子规模，每一个粒子代表一个解
Wmax=0.9;
Wmin=0.4;
%% 参数初始化
%粒子群算法中的两个参数
c1 = 2.0;
c2 = 2.0;
Vmax=20;                                        %最大速度
Vmin=-20;                                       %最小速度
popmax=100;                                    %最大值
popmin=0;                                      %最小值
yfitness=zeros(sizepop,2);                       %1行maxiter列矩阵，存放每一次迭代的最优值的空间矩阵
%% 产生初始粒子和速度
pop=[A(:,1), A(:,2)] ;                     %初始种群
for i=1:sizepop
   
    V(i,:)=rands(1,2)*5;                         %初始化速度
                    
end

%dist=Distance(pop(:,1),pop(:,2));  %初始距离
    %计算适应度
fitness=fun(pop(:,1),pop(:,2));      %粒子群的适应度
gbest=pop;                           %当前个体最优解向量组，矩阵
fitnessgbest=fitness;  
fitnesszbest=fitness;                %群体最优记录
yfitness=pop;
 %% 迭代寻优
for i=1:maxgen
    

    W=Wmax-((Wmax-Wmin)/maxgen)*i;
    for j=1:sizepop
        
        %速度更新
        V(j,:) = W*V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(yfitness(j,:) - pop(j,:));
     
    end 
    fitness(i)=fun(pop(:,1),pop(:,2));      %计算粒子群的适应度
         if fitness(i) > fitnessgbest
            gbest=pop;
           fitnessgbest(i)=fitness(i);
        end
        %群体极值更新
        if fitness(i)>fitnesszbest
            yfitness=pop;
            fitnesszbest(i)=fitness(i);    
        end
    
    %dist=Distance(pop(:,1),pop(:,2));
    zz(i)=max(fitnesszbest);
    
end
zbest=max(zz);
%% 结果分析
figure(1);
plot(zz) %画出迭代图
set(gcf,'color','w'); 
title('算法训练过程','fontsize',12);
xlabel('迭代次数','fontsize',12);
ylabel('覆盖率','fontsize',12);

%% 图形输出
figure(2)
plot(yfitness(:,1),yfitness(:,2),'+')

hold on


 
end
a=[yfitness(:,1),yfitness(:,2)]
set(gcf,'color','w'); 
% 窗口显示
disp([zbest]    );
toc
function z=fun(x,y)
%x input  圆心横坐标
%y input  圆心纵坐标
%z  output 覆盖率
L=100; % 正方形区域边长
R=12; % 圆半径
[m,n]=meshgrid(1:L);
Ar=linspace(0,pi*2,200); % 圆周角度
for i=1:30
D=sqrt([m-x(i)].^2+[n-y(i)].^2); % 计算坐标点到圆心的距离
[m0,n0]=find(D<=R); % 检测出圆覆盖点的坐标
Ind=sub2ind([L,L],m0,n0); % 坐标与索引转化
M(Ind)=1; % 改变覆盖状态
end
scale=sum(M(1:end))/L/L; % 计算覆盖比例

z=scale;

end



  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]张红霞.基于粒子群算法的无线传感器网络覆盖优化[J].现代电子技术. 2017,40(09)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/121221658