【图像融合】基于matlab GUI高斯金字塔+拉普拉斯金字塔彩色图像融合【含Matlab源码 1506期】

一、区域分割图像融合简介

图像的分解
对源图像进行融合时,首先对图像进行分解,利用拉普拉斯金字塔分解,先对图像进行高斯金字塔分解,然后再进行拉普拉斯金字塔分解。

1 高斯金字塔分解
记源图像为G0,G0即为高斯金字塔最底层,将其进行高斯低通滤波,之后对其进行隔行隔列的下采样,得到的图像与源图像在较低分辨率上近似,分辨率是源图的一半(高斯金字塔的第一层G1)。重复上述操作,得到下一层高斯金字塔。反复进行上述操作,得到若干层,即构成高斯金字塔。假设高斯金字塔的第l层图像为Gl:


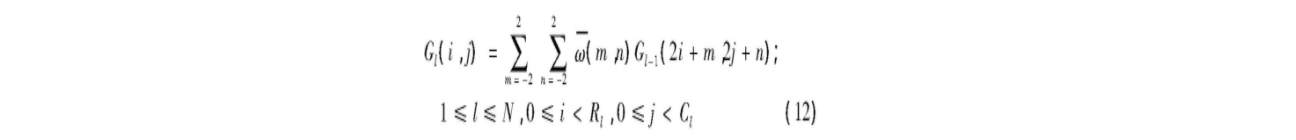
2 拉普拉斯金字塔分解
将上述得到的高斯金字塔利用插值法进行插值,膨胀后的图像Gl的尺寸与第l-1层图像Gl-1尺寸相同,如式(13)所示:

3 彩色图像融合
基于S-PCNN+局部熵(Local Entropy,LE)与拉普拉斯金字塔的融合,在一般RGB格式图像中,对每个分量进行处理时,由于三个分量的相关性很大,不易对特定因素进行处理,所以对图像进行融合时,为了得到较好的效果和有效的处理方式,先将RGB图像转换为HSI图像,得到H、S、I三个分量,再分别对三个分量进行相关的处理与融合。

对于H分量,送入S-PCNN模型,经过迭代得到振荡频图(Oscillation Frequency Graph,OFG),再对其得到的振荡频图(OFG)进行局部熵(LE)的计算,得到OFG局部熵矩阵作为H分量的特征矩阵,最后根据不同的源图像的H分量对应像素局部熵的大小,取其LE较大的像素作为最终融合所取的像素。

图像的局部熵由下式表述:

其中:Pk=h(k)/(m×n),m×n表示像素I(i,j)的邻域,h(k)表示邻域的直方图,pi为邻域的归一化直方图,K表示邻域像素的最大灰度值。

对于S分量和I分量,对其进行拉普拉斯金字塔分解,然后用不同的策略对经分解处理后的金字塔子层图像进行融合。在金字塔低层的图像,用局部熵来作为决策准则选取融合系数,高层金字塔图像通过S-PCNN模型来选取融合系数。本文采用的融合算法是基于简化脉冲耦合神经元的神经网络模型(S-PCNN),S-PCNN模型每次迭代后,经过判断每个像素对应的神经元是否点火,可以输出一幅二值脉冲图像,这些二值图像包含了图像的一些特征信息。在S-PCNN网络的N次迭代运算中,对每个图像I的像素I(i,j)对应的神经元N(i,j)发出脉冲进行统计后可得到一幅振荡频图(OFG),将OFG记为ION,则可用式(16)计算得到:

根据分析统计每个像素点的点火次数,再通过计算其局部熵(LE)来选取源图像的包含更多信息的更清晰区域,作为融合部分进行最终的图像融合。经S-PCNN模型迭代后的图可以展现图像的主要细节信息。

源图像经拉普拉斯金字塔分解,得到许多在不同空间频带上的子图像,由于在各个频带上的图像包含的特征和细节不同,所以对不同频带上的子图像进行融合时采用的融合策略也不相同。对金字塔的低层0~N,区域能量能衡量图像的质量,采用区域能量的方式选取系数。其计算公式如下:

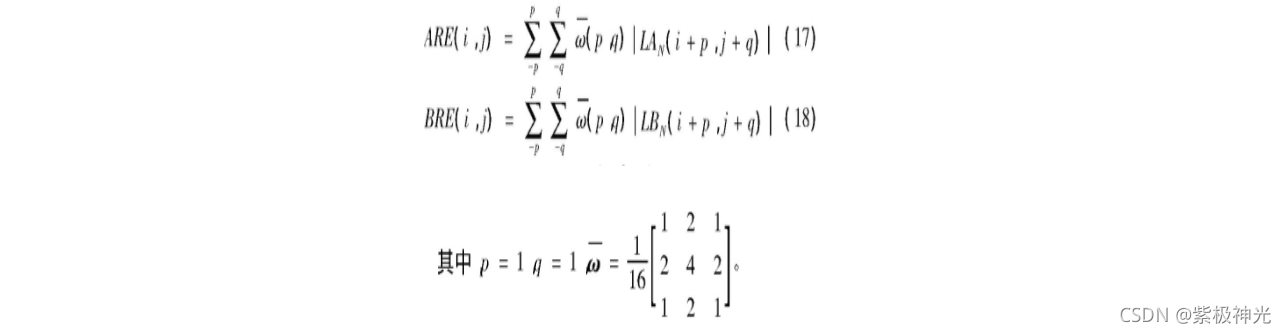
图像融合后的结果如下式所示:

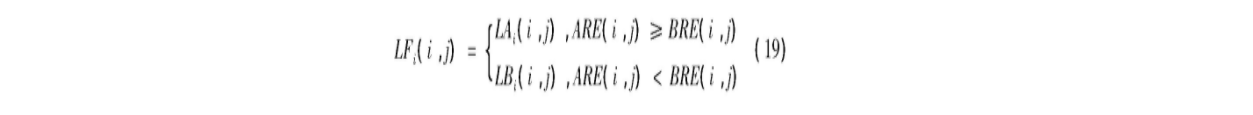
其中0≤l<N。
分别用上式计算获得金字塔的各层图像,融合后的图像LF1,LF2,LF3,…,LFN,通过式(14)可以重构出最终的融合图像。由于拉普拉斯金字塔高层图像含有源图像的细节信息及纹理和边缘信息,S-PCNN在提取图像纹理细节、区域分布等方面表现出色,所以对于高层的拉普拉斯金字塔图像则采用的S-PCNN模型来选取系数。
本文提出的彩色图像融合算法流程如图2所示。

图2 融合算法流程
结合算法流程,下面说明算法具体步骤:
1)将源彩色图像从RGB空间转换到HSI彩色空间,得到H、S、I三个分量。
2)将分离出的H分量送入S-PCNN模型,经过迭代后得到振荡频图(OFG);再对其进行局部熵(LE)的计算,得到OFG局部熵矩阵作为H分量的特征矩阵;最后根据不同源图像的H分量的对应像素的局部熵大小,取其LE较大的像素作为最终融合所取的像素。
3)将S、I分量进行拉普拉斯金字塔分解,对其用本文彩色图像融合部分表述的方式进行融合。
4)融合后的H、I、S分量得到HSI彩色图像,逆转换为RGB得到最终图像。

二、部分源代码

clear all;
clc;

leftImage = double(imread('apple.png'));
rightImage = double(imread('orange.png'));

iternum = 5;

if (size(leftImage) ~= size(rightImage))
    error('Input images are not the same size!')
end

% 预处理，使图片height,width为偶数
[rows, cols, channels] = size(leftImage);

% mask gaussian
mask = double(zeros(rows, cols, channels));
mask(:, 1:floor(cols/2), :) = ones(rows, floor(cols/2), channels);
mask_pyramid = GaussianPyramid(mask, iternum);


% leftImage pyramid and rightImage pyramid
left_pyramid = LaplacianPyramid(leftImage, iternum);
right_pyramid = LaplacianPyramid(rightImage, iternum);

% TODO: get blend laplacian pyramid
blend_pyramid = cell(iternum, 1);
for i = 1:iternum
    blend_pyramid{i} = left_pyramid{i} .* mask_pyramid{i} + right_pyramid{i} .* (1 - mask_pyramid{i});
end

% reconstruct the blend image
blendImage = LaplacianReconstruct(blend_pyramid);
imwrite(uint8(blendImage), 'blendImage.png');

figure;
imshow(uint8(leftImage));
title('leftImage');
figure;
imshow(uint8(rightImage));
title('rightImage');
figure;
imshow('blendImage.png');
title('blendImage');
function up_image=UpSampling(image)
    [rows, cols, channels] = size(image);
    up_image = double(zeros(rows*2, cols*2, channels));
    up_image(1:2:rows*2, 1:2:cols*2, :) = image;
%     up_image(2:2:rows*2, 2:2:cols*2, :) = image;
%     up_image(1:2:rows*2, 2:2:cols*2, :) = image;
%     up_image(2:2:rows*2, 1:2:cols*2, :) = image;




  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 蔡利梅.MATLAB图像处理——理论、算法与实例分析[M].清华大学出版社，2020.
[2]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社，2013.
[3]周品.MATLAB图像处理与图形用户界面设计[M].清华大学出版社，2013.
[4]刘成龙.精通MATLAB图像处理[M].清华大学出版社，2015.
[5]贺康建,金鑫,聂仁灿,周冬明,王佺,余介夫.基于简化脉冲耦合神经网络与拉普拉斯金字塔分解的彩色图像融合[J].

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/121254398