【优化算法】Tent映射的混合灰狼优化算法【含Matlab源码 1570期】

一、Tent映射的混合灰狼优化算法简介

1Ｔｅｎｔ 混沌映射
ＧＷＯ算法在解决函数优化问题中，通常利用随机产生的数据作为初始种群信息，这将难以保留种群的多样性，会造成算法的寻优结果较差． 然而，混沌运动具有随机性、规律性、以及遍历性的特征，在求解函数优化问题时这些特性能够使算法容易逃离局部最优解，从而可以维持种群的多样性，同时提高全局搜索能力． 现有的混沌映射有Ｔｅｎｔ 映 射、 Ｌｏｇｉｓｔｉｃ 映射等． 但是，不同的混沌映射对于提高函数优化能力不同． 目前文献中大多数采用 Ｌｏｇｉｓｔｉｃ 映射，但是该映射在［０， ０．１］和［０．９， １］两个区域内有较高的取值率． 因而，Ｌｏｇｉｓｔｉｃ 映射遍历不均匀性会导致算法的收敛速度较慢，从而导致算法的效率降低． 单梁［１５］等证明Ｔｅｎｔ 映射比 Ｌｏｇｉｓｔｉｃ 映射的遍历均匀性更好以及能够提高算法的寻优速度，与此同时能够在［０， １］之间产生分布较均匀的初始值． 因此，本文将利用 Ｔｅｎｔ 映射初始化种群． Ｔｅｎｔ 映射表达式：

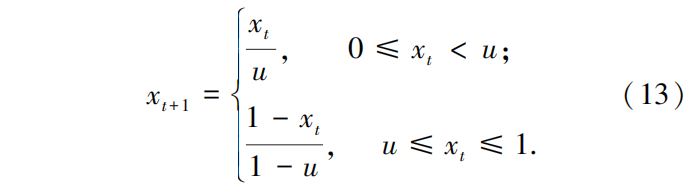
当 ｕ ＝ １ ／ ２ 时，Ｔｅｎｔ 映射具有最典型的形式，此时所得的序列具有均匀的分布，对不同的参数有近似一致的分布密度． 因而，本文引用的 Ｔｅｎｔ 混沌映射的公式为

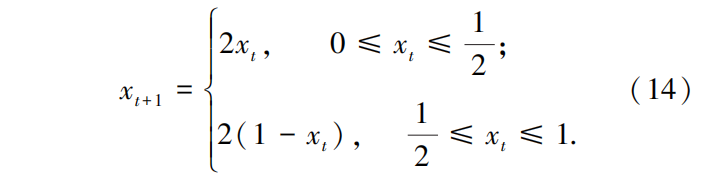
即 ｘｔ＋１ ＝ （２ｘｔ）ｍｏｄ１ Ｔｅｎｔ 混沌映射产生序列值的具体步骤如下所示：Ｓｔｅｐ１： 随机产生初始值 ｘ０（在［０，１］ 之间且避免 ｘ０ 落在 （０．２，０．４，０．６，０．８））， 记 入 标 记 组， 即 ｙ（１） ＝ｘ０ ，ｉ ＝ １，ｊ ＝ １； Ｓｔｅｐ２： 按式（１４） 迭代产生一个ｘ 序列，ｉ ＝ ｉ ＋ １；
Ｓｔｅｐ３：Ｉｆ 达到最大迭代次数，则转向 Ｓｔｅｐ４；Ｅｌｓｅ ｉｆ ｘｉ ＝ ｛０，０．２５，０．５，０．７５｝ 或者 ｘｉ ＝ ｘｉ － ｋ，ｋ ＝ ｛０，１，２， ３，４｝，则按式 ｘ（ｉ） ＝ ｙ（ｊ ＋ １） ＝ ｙ（ｊ） ＋ ｃ 改变迭代初值，ｃ是随机数，ｊ＝ｊ ＋ １； Ｅｌｓｅ 返回 Ｓｔｅｐ２； Ｓｔｅｐ４：运行停止，保留ｘ序列．

二、部分源代码

% PSO
% GWO
% IGWO
% PSO_GWO
%% 清空环境变量
clear
clc

%% 基本参数
N = 30;                    % 种群规模
maxgen = 500;         % 最大迭代次数

%% 获取函数名
Function_name = 'F4';   % 从F1到F23的测试函数的名称（本文中的表1、2、3）
[lb, ub, dim, fobj] = Get_Functions_details(Function_name);

%% 初始化种群位置
X = initialization(N, dim, ub, lb);
for i = 1:N
    fitness(i) = fobj(X(i, :));
end
cnt_max = 30;

curve_pso = zeros(1, maxgen);
curve_gwo = zeros(1, maxgen);
curve_igwo = zeros(1, maxgen);
curve_pso_gwo = zeros(1, maxgen);
for cnt = 1:cnt_max
    %% 传入函数变量
    [bestvalue_PSO, gbest_PSO, Curve_PSO] = PSO(N, maxgen, X, fitness, lb, ub, dim, fobj);
    [bestvalue_GWO, gbest_GWO, Curve_GWO] = GWO(N, maxgen, X, fitness, lb, ub, dim, fobj);
    [bestvalue_IGWO, gbest_IGWO, Curve_IGWO] = IGWO(N, maxgen, X, fitness, lb, ub, dim, fobj);
    [bestvalue_PSO_GWO, gbest_PSO_GWO, Curve_PSO_GWO] = PSO_GWO(N, maxgen, X, fitness, lb, ub, dim, fobj);
    %% 
    curve_pso = curve_pso + Curve_PSO;
    curve_gwo = curve_gwo + Curve_GWO;
    curve_igwo = curve_igwo + Curve_IGWO;
    curve_pso_gwo = curve_pso_gwo + Curve_PSO_GWO;
end
%% 绘图比较
figure;
t = 1:maxgen;
semilogy(t, curve_pso/cnt_max, 'bo-', t, curve_gwo/cnt_max, 'k*-', t, curve_igwo/cnt_max, 'mx-',...
    t, curve_pso_gwo/cnt_max, 'rd-', 'linewidth', 2, 'linewidth', 1.5, 'MarkerSize',7, 'MarkerIndices', 1:50:maxgen);
legend('PSO', 'GWO', 'IGWO', 'PSO\_GWO');
title('F3');
xlabel '迭代次数';
ylabel '目标函数值';


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/122029869