【路径规划】基于matlab模糊控制机器人路径规划【含Matlab源码 1643期】

一、模糊控制机器人路径规划简介

在未知环境下，针对传统模糊控制算法规划路径在某些复杂的障碍物环境中出现的死锁问题，设计了障碍逃脱策略，即当机器人进入陷阱区并在目标点方向不可行时，寻找可行方向并设置方向点，由方向点暂代目标点继续前行，沿方向点走出障碍物陷阱区后，则恢复原目标点。对于障碍逃脱策略无法走出的障碍物环境，进一步设计了转向策略，使机器人能成功走出陷阱区域，到达目标点。基于 MATLAB 仿真平台对所设计算法在不同环境下进行了测试和比较。结果验证了所设计算法的可行性和有效性。

二、部分源代码

function [Distance,Flag]=GetMinDistance(DectLineK, DectLineB, DectLineF,PgoalXnew,PgoalYnew)
%Distance 为最短距离，Flag表征其有效性 0 无  1有 2异常
%依据测量线斜率情况及走向 选择出交涉区域的障碍，及夹角取向
global CirX;
global CirY; 
global CirR; 
global ProbotX; 
global ProbotY;

    if DectLineF ==1 
        if ProbotY < PgoalYnew  %竖直向上运动
            Ydown=PgoalYnew;
            Yup  =PgoalY;

        else
            Ydown=PgoalYnew;
            Yup  =ProbotY;  

        end      
        IndexX= ((ProbotX-CirR) < CirX) & (CirX < (ProbotX+CirR));
        IndexY= (Ydown < CirY) & (CirY < Yup);
        IndexALL=IndexX & IndexY;
        
    elseif DectLineF == 2
        if ProbotX < PgoalXnew  %水平向右运动
            Xleft = ProbotX;
            Xright= PgoalXnew;

        else
            Xleft = PgoalXnew;
            Xright= ProbotX;  
        end
        IndexX= (Xleft < CirX) & (CirX < Xright);
        IndexY= ((ProbotY-CirR) < CirX) & (CirX < (ProbotY+CirR));
        IndexALL=IndexX & IndexY;    
        
    else
        AngelDectLine=atan(DectLineK);
        if DectLineK > 0            
            if ProbotX < PgoalXnew  %正斜率向上运动
                Xleft = ProbotX;
                Yleft = ProbotY;
                Xright= PgoalXnew;                
                Yright= PgoalYnew; 

            else                 %正斜率向下运动
                Xleft = PgoalXnew;
                Yleft = PgoalYnew;
                Xright= ProbotX;                
                Yright= ProbotY;    
                
            end   
            LineBleft = Yleft + Xleft/DectLineK;
            LineBright= Yright + Xright/DectLineK;
            Btemp=CirR/cos(AngelDectLine);
            Xtemp=CirR*sin(AngelDectLine);             
            LineBup  = DectLineB +Btemp;
            LineBdown= DectLineB -Btemp;
            X1=Xleft-Xtemp;
            X2=Xleft+Xtemp;
            X3=Xright-Xtemp;
            X4=Xright+Xtemp;
            IndexX1= (X1 < CirX) & (CirX < X2);
            IndexX2= (X2 < CirX) & (CirX < X3); 
            IndexX3= (X3 < CirX) & (CirX < X4);
            Ytemp=CirX/DectLineK;
            Y1=LineBleft-Ytemp;  %与斜率垂直的左右两条直线
            Y2=LineBright-Ytemp;
            Ytemp=CirX*DectLineK;
            Y3=LineBup  +Ytemp; %与斜率平行的上下两条直线
            Y4=LineBdown+Ytemp;
            IndexY1= (Y1 < CirY) & (CirY < Y3);
            IndexY2= (Y4 < CirY) & (CirY < Y3);
            IndexY3= (Y4 < CirY) & (CirY < Y2);
            
            IndexALL=(IndexX1 & IndexY1)|(IndexX2 & IndexY2)|(IndexX3 & IndexY3);  
            
        else 
            if ProbotX < PgoalXnew  %负斜率向 下运动
                Xleft = ProbotX;
                Yleft = ProbotY;
                Xright= PgoalXnew;                
                Yright= PgoalYnew;  

            else                 %负斜率向 上运动
                Xleft = PgoalXnew;
                Yleft = PgoalYnew;
                Xright= ProbotX;                 
                Yright= ProbotY;  

            end    
            
            LineBleft = Yleft + Xleft/DectLineK;
            LineBright= Yright + Xright/DectLineK;
            Btemp=CirR/cos(AngelDectLine);   %平行线的截矩
            Xtemp=CirR*sin(-AngelDectLine);  %注意加负号           
            LineBup  = DectLineB +Btemp;
            LineBdown= DectLineB -Btemp;
            X1=Xleft-Xtemp;
            X2=Xleft+Xtemp;
            X3=Xright-Xtemp;
            X4=Xright+Xtemp;
            IndexX1= (X1 < CirX) & (CirX < X2);
            IndexX2= (X2 < CirX) & (CirX < X3); 
            IndexX3= (X3 < CirX) & (CirX < X4);
            Ytemp=CirX/DectLineK;
            Y1=LineBleft-Ytemp;  %与斜率垂直的左右两条直线
            Y2=LineBright-Ytemp;
            Ytemp=CirX*DectLineK;
            Y3=LineBup  +Ytemp; %与斜率平行的上下两条直线
            Y4=LineBdown+Ytemp;
            IndexY1= (Y4 < CirY) & (CirY < Y1);
            IndexY2= (Y4 < CirY) & (CirY < Y3);
            IndexY3= (Y2 < CirY) & (CirY < Y3);
            
            IndexALL=(IndexX1 & IndexY1)|(IndexX2 & IndexY2)|(IndexX3 & IndexY3);              
        end        
    end
     
    %如果没有找出，机器可直达目标，穿越障碍成功，结束探测
    CheckX=CirX(IndexALL);   
    if isempty(CheckX) 
        Distance =0;
        Flag=0;
        return;
    end    
    
    CirXt=CirX(IndexALL);   %此时可能有多个
    CirYt=CirY(IndexALL); 
    CirRt=CirR(IndexALL);     

        

    if DProbotToBar < 0 %出现严重异常
        Distance =0;
        Flag=2;
    else
        Distance =DProbotToBar;
        Flag=1;              
    end

        


  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
 

三、运行结果

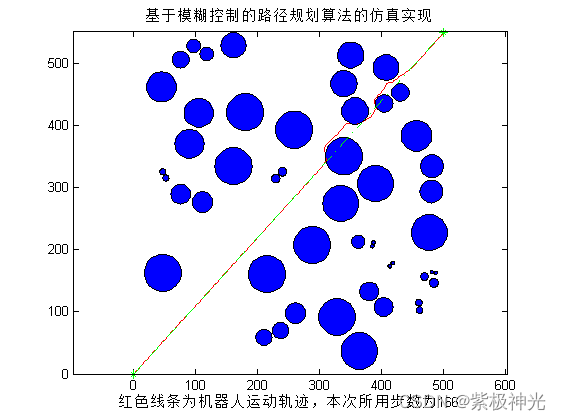
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]郭娜,李彩虹,王迪,张宁,宋莉.基于模糊控制的移动机器人局部路径规划[J].山东理工大学学报(自 然 科 学 版)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/122156899