【KELM回归预测】基于matlab麻雀算法SSA优化KELM回归预测【含Matlab源码 1646期】

举报
海神之光 发表于 2022/05/28 22:59:59 2022/05/28
【摘要】 一、混合核KELM简介 KELM是由Huang等（2006）开发的单隐层前馈神经网络（SLFN），它将核函数引入原ELM，保证了网络具有良好的泛化特性和较快的学习速度，其在一定程度上改善了传统梯度下降训...

一、混合核KELM简介

KELM是由Huang等（2006）开发的单隐层前馈神经网络（SLFN），它将核函数引入原ELM，保证了网络具有良好的泛化特性和较快的学习速度，其在一定程度上改善了传统梯度下降训练算法中存在的局部最优以及迭代次数大的缺点，将线性不可分离模式映射到高维特征空间，以获得线性可分离性和精度方面的改进性能。
在这里插入图片描述
其中，x 代表样本，f (x) 为神经网络的输出，h(x) 或 H 表示隐藏层特征映射矩阵，β 表示隐藏层和输出层之间的权重。 β 的公式如下:
在这里插入图片描述
其中，T 表示训练样本的目标向量，I 为单位矩阵，C为正则化参数。只要对特征 h(x) 的映射拥有少量的知识，就可以使用一个称为内核的函数，如下所示:
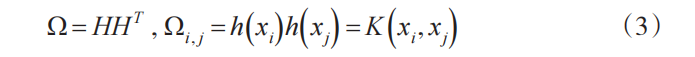
在这里插入图片描述
使用式（2）和式（3），式（1）可以改写为：
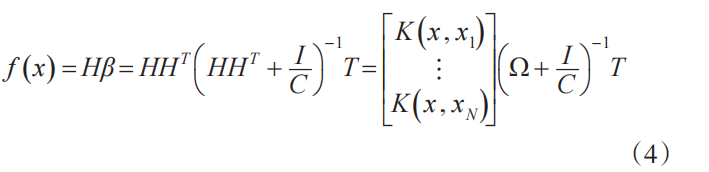
在这里插入图片描述
在核函数中，径向基函数（RBF）是被学者们广泛使用的函数之一。 RBF内核可以定义为：
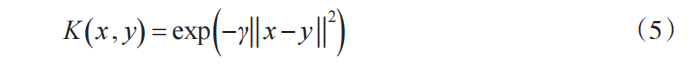
在这里插入图片描述
其中，γ 是内核参数。由于KELM模型的结果在很大程度上取决于正则化参数 C 和核参数 γ 的选择，因此需要有效地优化这两个参数。

二、部分源代码

%% 此程序为 粒子群优化混合核极限学习机回归预测
clear;clc;close all;warning off;rng(0)
format compact
%% 加载数据
data=xlsread('数据.xlsx','C2:F1166');
n_samples=size(data,1);
% n=randperm(n_samples);%随机70%训练剩下30%测试
n=1:n_samples;%前70%作为训练集  后30%测试集
m=floor(0.7*n_samples);
input_train=data(n(1:m),1:end-1);
output_train=data(n(1:m),end);
input_test=data(n(m+1:end),1:end-1);
output_test=data(n(m+1:end),end);
%% 2.数据归一化
%输入输出数据归一化
[inputn,inputps]=mapminmax(input_train',-1,1);%归一化到-1 1区间
[outputn, outputps]=mapminmax(output_train',-1,1);
inputn_test=mapminmax('apply',input_test',inputps);%测试集输入也采用训练集输入的归一化参数进行归一化
outputn_test=mapminmax('apply',output_test',outputps);%测试集输出也采用训练集输出的归一化参数进行归一化
P_train=inputn';
T_train=outputn';
P_test=inputn_test';
T_test=outputn_test';
%% 正则化系数与核参数进行设置
%核函数类型1.RBF_kernel 2.lin_kernel 3 poly_kernel 4 wav_kernel
kernel1='RBF_kernel';
kernel2='RBF_kernel';
% 对kernel1的权重w（kernel2的权重为1-w），正则化系数lambda与核参数ker1 ker2寻优
[pop,trace,process]=ssa_hkelm(kernel1,kernel2,P_train,T_train,P_test,T_test);
figure;plot(trace);xlabel('寻优次数/代');grid on;ylabel('适应度值/mse');title('适应度曲线')
% 核参数设置  详情看kernel_matrix
if strcmp(kernel1,'RBF_kernel') & strcmp(kernel2,'RBF_kernel')
    w=pop(1);lambda=pop(2);ker1=pop(3); ker2=pop(4); 
elseif strcmp(kernel1,'RBF_kernel') & strcmp(kernel2,'lin_kernel')
    w=pop(1);lambda=pop(2);ker1=pop(3); ker2=[];
elseif strcmp(kernel1,'RBF_kernel') & strcmp(kernel2,'poly_kernel')
    w=pop(1);lambda=pop(2);ker1=pop(3); ker2=pop(4:5); 
elseif strcmp(kernel1,'RBF_kernel') & strcmp(kernel2,'wav_kernel')
    w=pop(1);lambda=pop(2);ker1=pop(3); ker2=pop(4:6); 
elseif strcmp(kernel1,'lin_kernel') & strcmp(kernel2,'lin_kernel')
    w=pop(1);lambda=pop(2);ker1=[]; ker2=[]; 
elseif strcmp(kernel1,'lin_kernel') & strcmp(kernel2,'poly_kernel')
    w=pop(1);lambda=pop(2);ker1=[]; ker2=pop(3:4); 
elseif strcmp(kernel1,'lin_kernel') & strcmp(kernel2,'wav_kernel')
    w=pop(1);lambda=pop(2);ker1=[]; ker2=(3:5); 
elseif strcmp(kernel1,'poly_kernel') & strcmp(kernel2,'poly_kernel')
    w=pop(1);lambda=pop(2);ker1=pop(3:4); ker2=pop(5:6); 
elseif strcmp(kernel1,'poly_kernel') & strcmp(kernel2,'wav_kernel')
    w=pop(1);lambda=pop(2);ker1=pop(3:4); ker2=pop(5:7); 
elseif strcmp(kernel1,'wav_kernel') & strcmp(kernel2,'wav_kernel')
    w=pop(1);lambda=pop(2);ker1=pop(3:5); ker2=pop(6:8);    
end
function valError= fitness(pop,kernel1,kernel2,XTrain,YTrain,XValidation,YValidation)
% 核参数设置  详情看kernel_matrix
if strcmp(kernel1,'RBF_kernel') & strcmp(kernel2,'RBF_kernel')
    w=pop(1);lambda=pop(2);ker1=pop(3); ker2=pop(4); 
elseif strcmp(kernel1,'RBF_kernel') & strcmp(kernel2,'lin_kernel')
    w=pop(1);lambda=pop(2);ker1=pop(3); ker2=[];
elseif strcmp(kernel1,'RBF_kernel') & strcmp(kernel2,'poly_kernel')
    w=pop(1);lambda=pop(2);ker1=pop(3); ker2=pop(4:5); 
elseif strcmp(kernel1,'RBF_kernel') & strcmp(kernel2,'wav_kernel')
    w=pop(1);lambda=pop(2);ker1=pop(3); ker2=pop(4:6); 
elseif strcmp(kernel1,'lin_kernel') & strcmp(kernel2,'lin_kernel')
    w=pop(1);lambda=pop(2);ker1=[]; ker2=[]; 
elseif strcmp(kernel1,'lin_kernel') & strcmp(kernel2,'poly_kernel')
    w=pop(1);lambda=pop(2);ker1=[]; ker2=pop(3:4); 
elseif strcmp(kernel1,'lin_kernel') & strcmp(kernel2,'wav_kernel')
    w=pop(1);lambda=pop(2);ker1=[]; ker2=(3:5); 
elseif strcmp(kernel1,'poly_kernel') & strcmp(kernel2,'poly_kernel')
    w=pop(1);lambda=pop(2);ker1=pop(3:4); ker2=pop(5:6); 
elseif strcmp(kernel1,'poly_kernel') & strcmp(kernel2,'wav_kernel')
    w=pop(1);lambda=pop(2);ker1=pop(3:4); ker2=pop(5:7); 
elseif strcmp(kernel1,'wav_kernel') & strcmp(kernel2,'wav_kernel')
    w=pop(1);lambda=pop(2);ker1=pop(3:5); ker2=pop(6:8);    
end
% 训练核极限学习机
% 训练过程
n=size(XTrain,1);%样本数
Omega_1 = kernel_matrix(XTrain,kernel1, ker1);%隐含层输出
Omega_2 = kernel_matrix(XTrain,kernel2, ker2);%隐含层输出
Omega_train=w*Omega_1+(1-w)*Omega_2;

OutputWeight=((Omega_train+speye(n)/lambda)\(YTrain));

% 测试过程
Omega_1_test = kernel_matrix(XTrain,kernel1, ker1,XValidation);
Omega_2_test = kernel_matrix(XTrain,kernel2, ker2,XValidation);
Omega_test=w*Omega_1_test+(1-w)*Omega_2_test;
Y2=Omega_test' * OutputWeight;
[m,n]=size(Y2);
YPred=reshape(Y2,[1,m*n]);
YReal=reshape(YValidation,[1,m*n]);

valError =mse(YPred-YReal);
function result(true_value,predict_value,type)
disp(type)
rmse=sqrt(mean((true_value-predict_value).^2));
disp(['根均方差(RMSE)：',num2str(rmse)])
mae=mean(abs(true_value-predict_value));
disp(['平均绝对误差（MAE）：',num2str(mae)])
mape=mean(abs((true_value-predict_value)./true_value));
disp(['平均相对百分误差（MAPE）：',num2str(mape*100),'%'])
r2 = R2(predict_value, true_value);
disp(['R平方决定系数（MAPE）：',num2str(r2)])
nse = NSE(predict_value, true_value);
disp(['纳什系数（NSE）：',num2str(nse)])



fprintf('\n')

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    • 
  
  • 40
    • 
  
  • 41
    • 
  
  • 42
    • 
  
  • 43
    • 
  
  • 44
    • 
  
  • 45
    • 
  
  • 46
    • 
  
  • 47
    • 
  
  • 48
    • 
  
  • 49
    • 
  
  • 50
    • 
  
  • 51
    • 
  
  • 52
    • 
  
  • 53
    • 
  
  • 54
    • 
  
  • 55
    • 
  
  • 56
    • 
  
  • 57
    • 
  
  • 58
    • 
  
  • 59
    • 
  
  • 60
    • 
  
  • 61
    • 
  
  • 62
    • 
  
  • 63
    • 
  
  • 64
    • 
  
  • 65
    • 
  
  • 66
    • 
  
  • 67
    • 
  
  • 68
    • 
  
  • 69
    • 
  
  • 70
    • 
  
  • 71
    • 
  
  • 72
    • 
  
  • 73
    • 
  
  • 74
    • 
  
  • 75
    • 
  
  • 76
    • 
  
  • 77
    • 
  
  • 78
    • 
  
  • 79
    • 
  
  • 80
    • 
  
  • 81
    • 
  
  • 82
    • 
  
  • 83
    • 
  
  • 84
    • 
  
  • 85
    • 
  
  • 86
    • 
  
  • 87
    • 
  
  • 88
    • 
  
  • 89
    • 
  
  • 90
    • 
  
  • 91
    • 
  
  • 92
    • 
  
  • 93
    • 
  
  • 94
    • 
  
  • 95
    • 
  
  • 96
    • 
  
  • 97
    • 
  
  • 98
    • 
  
  • 99
    • 
  
  • 100
    • 
  
  • 101
    • 
  
  • 102
    • 
  
  • 103
    • 
  
  • 104
    • 
  
  • 105
    • 
  
  • 106
    • 
  
  • 107
    • 
  
  • 108
    • 
  
  • 109
    • 
  
  • 110
    •

三、运行结果

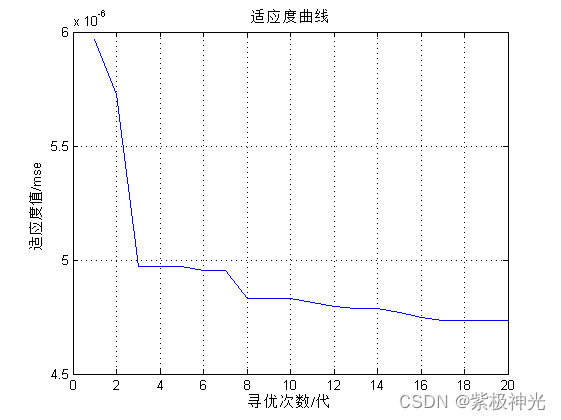
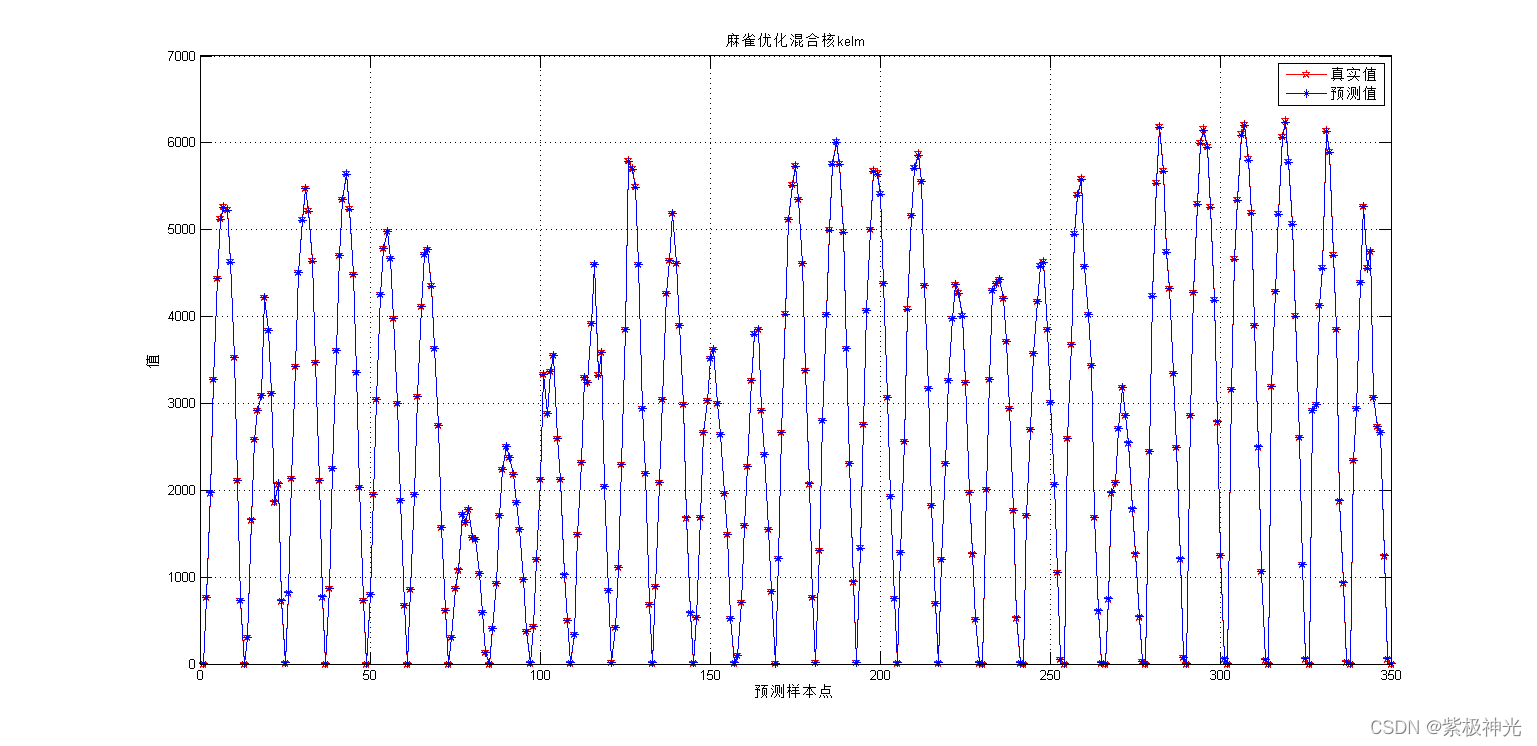
在这里插入图片描述
在这里插入图片描述

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.
[6]张婷婷,唐振鹏,吴俊传.基于优化KELM模型的股票指数预测方法[J].统计与决策. 2021,37(13)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/122156432

【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
MATLAB 机器学习
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入