【目标定位】基于matlab去偏卡尔曼滤波目标定位仿真【含Matlab源码 140期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【目标定位】基于matlab去偏卡尔曼滤波目标定位仿真【含Matlab源码 140期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、EKF算法简介

在SLAM问题解决方法中，EKF算法是比较常用的经典算法。机器人的自定位过程是一个非线性化的过程，EKF是为了解决Kalman滤波器不能应用于非线性系统而产生的，该滤波算法的主要过程是预测和更新。在预测和更新过程中，EKF算法对原有的系统方程和观测方程进行线性化并得到一个高估计的结果。如果系统中的非线性很弱，EKF也能给出很好的估计结果。

预测时，使用系统模型如下：

式中，z(k+1）表示的是第k+1步中获得的观测量，W （k+1）表示Kalman增益，其中还包括了前向估计在实际中的权重。

实现EKF-SLAM需要以下几方面内容：系统动态方程以及相应的参量，使用的传感器类型和观测方程，根据这些可以得到EKF的相应形式。二维平面中的EKF-SLAM需要知道机器人在X、Y方向的值，还需要知道二维平面下机器人头部朝向与X轴正方向的夹角。

三、部分源代码

clc;
clear;
N1=100;
thita=1*pi/4;
speed=20;
T=2.5;
point_Q2=[400 0;0 1*pi^2/180^2];
%Q1=[0.36 0;0 0];     %添加机动情形
%Q1=[0 0;0 0];        %不添加机动
l=[1/2*T^2 0;T 0;0 1/2*T^2;0 T];
N=200;
r=1000;
r_thita=1/3*pi;
object_init_state=[r*cos(r_thita) speed*cos(thita) r*sin(r_thita) speed*sin(thita)];   
for i=1:N1
    [real_data,view_data,real_v,Q1,point_view_data]=new_data_get(object_init_state,N,T,l);                   
    %前条件：目标的初始状态，目标跟踪次数已知
    %后条件：得到目标的观测矩阵，目标的真实值矩阵,真实速度
    [filter_data,k1,k2]=data_kalman_filter(view_data,point_view_data,N,object_init_state,Q1,point_Q2,T,l);
    %前条件：目标的观测矩阵已知
    %后条件：得到目标的滤波矩阵和目标的各次增益
    filt_k1(i,:,:)=k1;
    filt_k2(i,:,:)=k2;
    [ME_temp_view_err_x(i,1:N),ME_temp_filter_err_x(i,1:N),ME_temp_view_err_y(i,1:N),ME_temp_filter_err_y(i,1:N)]=temp_err_save(real_data,...
    filter_data,view_data);
    %前条件：目标的真实值矩阵，目标的滤波矩阵，目标的观测矩阵已知
    %后条件：本次目标的观测误差，滤波误差得到存储
end
[final_filt_k1,final_filt_k2]=filt_count(filt_k1,filt_k2,N1);
%前条件：得到增益的三维矩阵
%后条件：求出平均增益
[ME_final_view_err_x,ME_final_filter_err_x,ME_final_view_err_y,ME_final_filter_err_y]=ME_err_count(ME_temp_view_err_x,ME_temp_filter_err_x,...
ME_temp_view_err_y,ME_temp_filter_err_y);
%前条件：目标的观测误差矩阵，目标的滤波误差矩阵已知
%后条件：得到目标的平均观测误差矩阵，平均滤波误差矩阵
[RMSE_final_view_err_x,RMSE_final_filter_err_x,RMSE_final_view_err_y,RMSE_final_filter_err_y]=RMSE_err_count(ME_temp_view_err_x,...
ME_temp_filter_err_x,ME_temp_view_err_y,ME_temp_filter_err_y,ME_final_view_err_x,ME_final_filter_err_x,ME_final_view_err_y,ME_final_filter_err_y);
%后条件：得到目标的均方观测误差矩阵，均方滤波误差矩阵
%show(ME_final_view_err_x,ME_final_filter_err_x,ME_final_view_err_y,ME_final_filter_err_y,final_filt_k1,final_filt_k2,N,real_data,view_data,filter_data,real_v);
show(ME_final_view_err_x,ME_final_filter_err_x,ME_final_view_err_y,ME_final_filter_err_y,RMSE_final_view_err_x,RMSE_final_filter_err_x,...
RMSE_final_view_err_y,RMSE_final_filter_err_y,final_filt_k1,final_filt_k2,N,real_data,view_data,filter_data,real_v);
%前条件：目标的平均观测误差矩阵，平均滤波误差矩阵已知
%后条件：作出目标的平均观测误差矩阵，平均滤波误差矩阵的仿真图
function [filter_data,k1,k2]=data_kalman_filter(view_data,point_view_data,N,object_init_state,Q1,point_Q2,T,l)
%定义初试滤波
filter_data0=object_init_state';
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
ch=[1 T 0 0;0 1 0 0;0 0 1 T;0 0 0 1];               %定义状态转移矩阵

h=[1 0 0 0;0 0 1 0];                               %观测转移矩阵
%观测误差是随时间变化的所以需计算观测误差
cos_2_v_thita=(object_init_state(1,1)^2)/(object_init_state(1,1)^2+object_init_state(1,3)^2);
sin_2_v_thita=1-cos_2_v_thita;
R_2=(object_init_state(1,1)^2+object_init_state(1,3)^2);
Q2=zeros(2,2);       
Q2(1,1)=point_Q2(1,1)*cos_2_v_thita+R_2*sin_2_v_thita*point_Q2(2,2);
%Q2(1,2)=sqrt(cos_2_v_thita)*sqrt(sin_2_v_thita)*(point_Q2(1,1)-R_2*point_Q2(2,2));
Q2(1,2)=0;
Q2(2,1)=Q2(1,2);
Q2(2,2)=point_Q2(1,1)*sin_2_v_thita+R_2*cos_2_v_thita*point_Q2(2,2);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%    
pre_data(:,1)=ch*filter_data0;
p_init=100*eye(4);                                                   %初始协方差定义 
p_old=p_init;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%根据初始预测计算滤波值
%通过输入观测值进行卡尔曼滤波
for i=1:N
    [filter_data(:,i),pre_data(:,i+1),p_new,k11,k21,Q2]=kalman_filter(pre_data(:,i),view_data(:,i),point_view_data(:,i),p_old,ch,Q1,Q2,h,l,point_Q2);
    p_old=p_new;
    k1(:,i)=k11;
    k2(:,i)=k21;
end
%function show(ME_final_view_err_x,ME_final_filter_err_x,ME_final_view_err_y,ME_final_filter_err_y,final_filt_k1,final_filt_k2,N,real_data,view_data,filter_data,real_v);
function show(ME_final_view_err_x,ME_final_filter_err_x,ME_final_view_err_y,ME_final_filter_err_y,RMSE_final_view_err_x,RMSE_final_filter_err_x,RMSE_final_view_err_y,RMSE_final_filter_err_y,final_filt_k1,final_filt_k2,N,real_data,view_data,filter_data,real_v)
M=1:N;
figure('NumberTitle','off','name','x方向均值误差比较图');
plot(M,ME_final_view_err_x,':r'),hold on
plot(M,ME_final_filter_err_x);
grid on;
figure('NumberTitle','off','name','y方向均值误差比较图'); 
plot(M,ME_final_view_err_y,':r'),hold on
plot(M,ME_final_filter_err_y);
grid on;
figure('NumberTitle','off','name','x方向均方误差比较图');
plot(M,RMSE_final_view_err_x,':r'),hold on
plot(M,RMSE_final_filter_err_x);
grid on;
figure('NumberTitle','off','name','y方向均方误差比较图'); 
plot(M,RMSE_final_view_err_y,':r'),hold on
plot(M,RMSE_final_filter_err_y);
grid on;
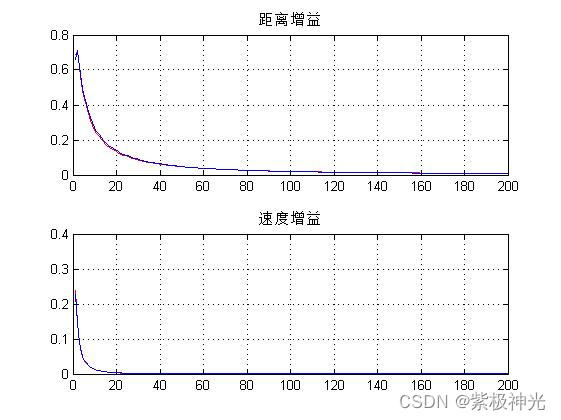
figure('NumberTitle','off','name','增益图');
subplot(2,1,1),plot(M,final_filt_k1(1,:),'r');
hold on;
plot(M,final_filt_k2(3,:))
title('距离增益')
grid on;
subplot(2,1,2),plot(M,final_filt_k1(2,:),'r');
hold on;
plot(M,final_filt_k2(4,:));
title('速度增益')
grid on
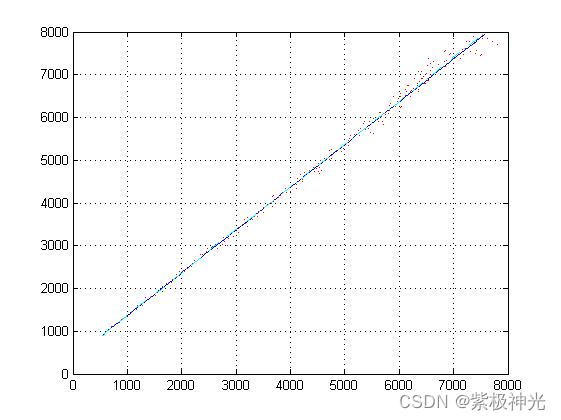
figure('NumberTitle','off','name','轨迹图');
plot(real_data(1,:),real_data(2,:)),hold on
plot(view_data(1,:),view_data(2,:),':r'),hold on
plot(filter_data(1,:),filter_data(3,:),'-.c')
grid on
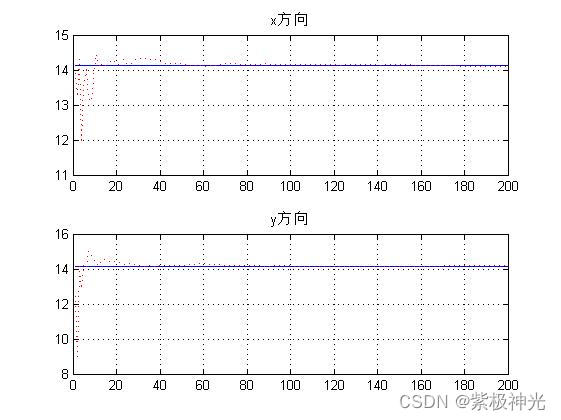
figure('NumberTitle','off','name','速度图');
subplot(2,1,1),plot(M,real_v(1,:)),hold on
plot(M,filter_data(2,:),':r');
title('x方向')
grid on;
subplot(2,1,2),plot(M,real_v(2,:)),hold on
plot(M,filter_data(4,:),':r');
title('y方向')
grid on;

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
 

四、运行结果

运行结果各图名称见实际运行的命名；

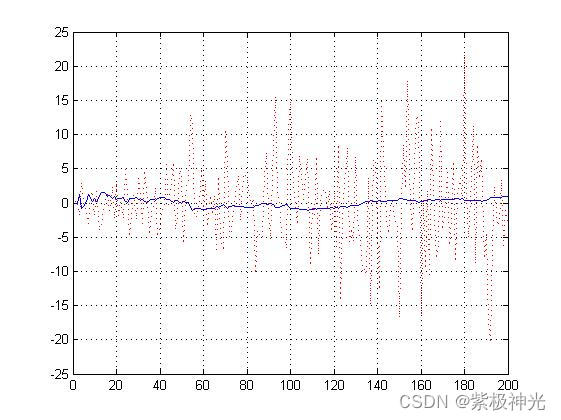
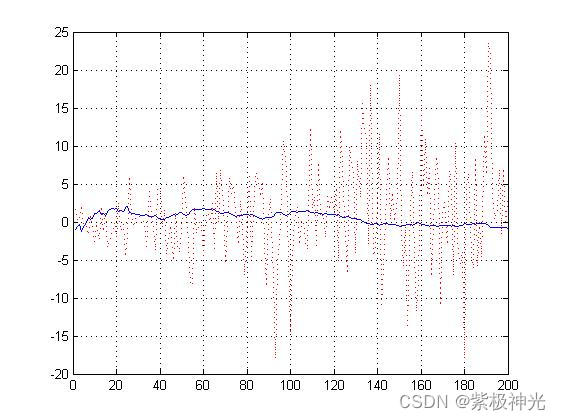
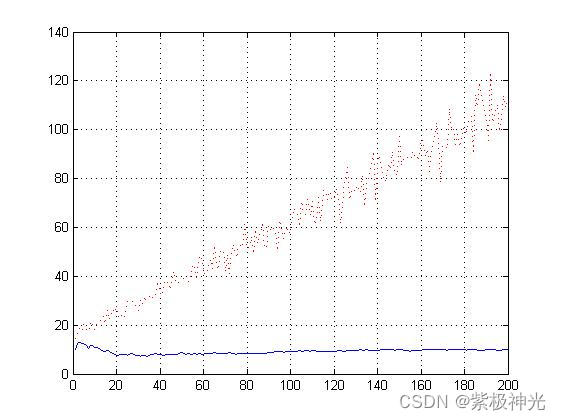
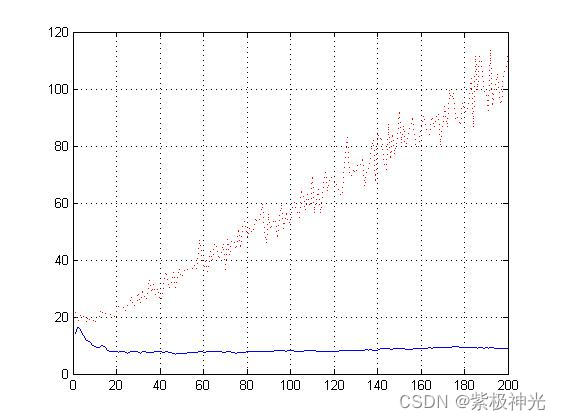
五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 沈再阳.精通MATLAB信号处理[M].清华大学出版社，2015.
[2]高宝建,彭进业,王琳,潘建寿.信号与系统——使用MATLAB分析与实现[M].清华大学出版社，2020.
[3]王文光,魏少明,任欣.信号处理与系统分析的MATLAB实现[M].电子工业出版社，2018.
[4]林志东.基于扩展卡尔曼滤波算法的SLAM问题分析[J].城市建筑. 2020,17(11)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/122195930