【数字信号去噪】基于matlab小波软阈值+硬阈值+改进的阈值高斯脉冲信号去噪【含Matlab源码 1706期】

一、小波阈值法去噪概述

电能质量扰动信号的噪声大多以高斯白噪声的形式存在，利用小波变换对信号进行多分辨率分解，由于小波变换具有去除数据相关性的特点，故可以将有用信号与噪声的能量分离开来。信号中有效的信息主要集中在较大的小波系数上，而噪声大多分布在较小的系数中，因此通过设置阈值可以将低于该阈值的系数当做噪声去除从而达到滤波的目的。

假设一个线性非平稳并含噪的一维信号表达式如下:

其中，f(t)为原始信号，ε(t)为高斯白噪声，x(t)为含噪信号。接着根据该信号的特点，采用合适的小波基和分解层数，对x(t)进行一维离散小波变换:

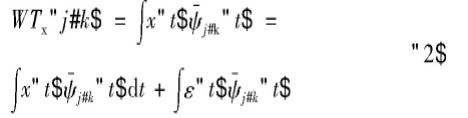
其中，ψ(t)为离散小波尺度函数。式(2)对应的小波系数表达式为:

其中，dj,k为含噪信号x(t)经过小波变换多尺度分解后的各层小波细节系数，uj,k与ej,k分别为原始信号f(t)和噪声信号ε(t)经过小波变换多尺度分解后的细节系数。基于小波阈值去噪的流程图如图1所示。

图1 小波去噪流程
小波阈值去噪的具体步骤如下:

(1)多尺度分解:根据含噪信号的特点选择适合的小波基和分解层数，经过离散小波变换得到各层的小波细节系数dj,k;

(2)阈值去噪:通过确定阈值λ和阈值函数对小波细节系数dj,k进行处理，得到处理后的各层小波细节系数d’j,k;

(3)小波重构:依据得到的小波细节系数d’j,k和近似系数对电能质量扰动信号进行重构，得到去噪后的扰动信号x’(t)。

这些步骤中，阈值和阈值函数的选择是小波阈值去噪的关键，直接影响着重构信号的质量。如果选择的阈值过大，则会导致有用的信号被当做噪声滤除;阈值过小，则导致噪声的滤除不够彻底。传统的硬、软阈值函数如下所示:

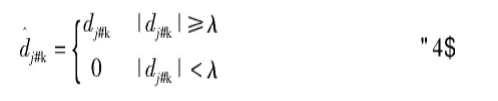
软阈值函数的定义:

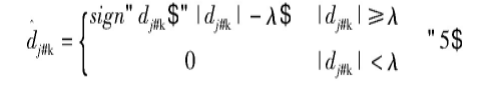
式中sign(dj,k)为符号函数，,N为信号长度;σ=Mmid/0.6745,Mmid是最低层小波系数的中位数。根据硬、软阈值函数可以看出，对含噪信号进行小波多尺度分解后，将每一层的细节系数与阈值相比较，保留大于阈值的系数，将小于阈值的系数置零，由此得到去除噪声后的细节系数。但是，硬阈值函数在信号长度内不是连续的，在λ处存在间断点，使得重构的信号不够平滑，重构信号后会产生“吉布斯”现象。软阈值函数虽然保证了连续性的问题，但是其噪声估计值与真实值存在着固定的偏差，不仅容易造成噪声去除不够彻底，还可能会丢失部分有用的信息。

2 小波阈值去噪的改进方法
通过上一节对硬、软阈值的分析可知，传统小波阈值去噪方法对于各层的小波系数阈值的设置是恒定不变的，但是噪声在各层小波系数中都是不太相同的，因此采用固定的阈值其自适应性较差，去噪效果不太理想。为了解决上述的这些问题，提出了一种改进的小波阈值去噪算法，它会根据噪声的分布情况自适应的修正阈值，并且其阈值函数通过可变参数可以实现多种不同的软硬特征，使其更加适用于多种不同类型的电能质量扰动信号。

2.1 阈值的修正
阈值作为区分有效信息与噪声的边界，它的选择直接影响着去噪效果。传统的通用阈值对每个尺度的小波细节系数都做了同样的处理，但是噪声的分布具有随机性，用一个固定的阈值进行处理会使得有些尺度上的有用信息丢失，而有些尺度上的噪声滤除的不够干净，这样就无法达到较好的去噪效果。考虑到噪声的小波细节系数随尺度的增加而减小，而信号的小波细节系数随尺度的增加而增大。因此为了使阈值的取值更加符合噪声的变化规律，本章结合了文献[7]中的峰和比(peak-to-sum ratio,PSR)，提出了基于PSR的修正因子，对通用阈值进行修正，第j层小波细节系数的峰和比公式如下:

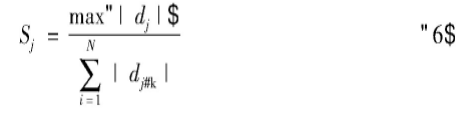
式中，dj,k是小波细节系数。在小波的多尺度分解中，信号的有用信息主要集中在较大的小波细节系数上，而噪声成分则分散在各层的小波细节系数中。因此，当Sj值较大时，意味着这一尺度存在着较大的系数，说明了该层包含的有用信息较多;而Sj值较小时，则意味者这一尺度存在着较小的系数，说明了该层包含的噪声较多。基于这一特点，则引入修正因子Fj为:

式中，Lj为第j层小波细节系数的长度。将Fj与ln(j+1)相结合来对阈值进行自适应调节。经过修正后的阈值为:

由式(8)可知，ln(j+1)随着j的增加逐渐增大，相应的阈值就逐渐减小，这符合噪声分布的一般规律。

2.2 改进阈值函数
为了克服传统硬阈值函数在阈值处不连续和软阈值函数会造成部分高频信息丢失的问题，提出了一种新的阈值函数如下所示:

式中sign函数为符号函数。该阈值函数在(-!，+!)内连续，证明如下:

该函数在λj处连续，同理可得函数在-λj处也是连续的。证明其确实克服了硬阈值函数在阈值处不连续的问题。并且该阈值函数在dj,k→±!时等效于硬阈值函数。证明如下:

由上式可以看出，随着小波细节系数dj,k的增加，新阈值函数曲线逐渐向硬阈值函数逼近，克服了软阈值函数所存在的恒定偏差的问题。新阈值函数的示意图如图2所示。

图2 新阈值函数曲线图
2.3 小波基与分解层数
应用小波变换对电能质量扰动信号进行去噪、突变点定位和特征提取时，小波基的选择至关重要，只有选择了合适的小波基，才能准确的对电能质量扰动进行分析。因此，在实际应用中，需要根据所选信号的特征来选择合适的小波基。

小波变换的实质是用一系列的小波函数去逼近原始信号的过程，对于同一个信号，选取不同的小波基，其小波变换后的结果也是不同的。对电能质量信号进行小波变换分析，根据其波形的特点，需要采用时域和频域同时具有良好的局部性，且对不规则的部分比较敏感的小波。通常利用传统的软、硬阈值函数来考察小波变换对信号去噪效果的影响。为了验证去噪效果，通常采用信噪比(Signal Noise Ratio,SNR)和均方根误差(Root Mean Square Error,RMSE)作为评价标准。其定义表达式如下所示:

当信噪比(SNR)越高，均方根误差(RMSE)越低时，就证明了该信号的去噪效果越好。这里选择电压中断扰动信号作为原始数据，通过将不同类型的小波基函数与软、硬阈值函数相结合来进行小波阈值去噪。

二、部分源代码

      close all;
clc;
clear;
format short g;
Fs=50*128;
N=2048;
l=1;
n=[0:1:N-1];
[y,t]=Gauss1(N,8);
figure(1)
plot(t,y);
xlabel('时间（ns）');
ylabel('信号功率（pw）');
title('原始信号');
axis([0, N-1,0, 1.2]);
s=awgn(y,1,'measured');% 加入高斯白噪
figure(2)
plot(s);
xlabel(' 时间（ns）');
ylabel('信号功率（pw）');
title('污染信号');
axis([0, N-1,-0.5, 1.5]);

%%--------------- 阈值选取 -------------------------
%生成不同的阈值
th1=thselect(s,'sqtwolog');
th2=thselect(s,'rigrsure');
th3=thselect(s,'heursure');
th4=thselect(s,'minimaxi');
fprintf('通用阈值th1: %4.4f\n',th1);
fprintf('Stein无偏风险阈值th2: %4.4f\n',th2);
fprintf('启发式阈值th3: %4.4f\n',th3);
fprintf('最大最小准则阈值th4: %4.4f\n',th4);


%%%--------------- 不同小波函数对去噪效果的影响 -------------------------
sym=['sym1';'sym2';'sym3';'sym4';'sym5';'sym6';'sym7';'sym8'];
db=['db1';'db2';'db3';'db4';'db5';'db6';'db7';'db8'];
coif=['coif1';'coif2';'coif3';'coif4';'coif5'];
[zwave(1,1:4),snrwave(1),snrsym]=levelandth(y,s,sym,8);
[zwave(2,1:3),snrwave(2),snrdb]=levelandth(y,s,db,8);
[zwave(3,1:5),snrwave(3),snrcoif]=levelandth(y,s,coif,5);
ksym=1:8;
kdb=1:8;
kcoif=1:5;
figure(12)
plot(ksym,snrsym,'r-',kdb,snrdb,'g-',kcoif,snrcoif,'b-'),grid on;
legend('sym小波系','db小波系','coif小波系');
xlabel('小波基');
ylabel(' 信噪比改善量（dB）');
title('不同小波函数能达到的最大信噪比改善量');
[snrwavemax,kwaxw]=max(snrwave);
fprintf(zwave(kwaxw,:));   
fs = 44100; 
dt = 1/fs;

T16 = 0.125;

t16 = [0:dt:T16];
[temp k] = size(t16);

t4 = linspace(0,4*T16,4*k);
t8 = linspace(0,2*T16,2*k);

[temp i] = size(t4);
[temp j] = size(t8);

mod4=(t4.^4).*exp(-30*(t4.^0.5));
mod4=mod4*(1/max(mod4));
mod8=(t8.^4).*exp(-50*(t8.^0.5));
mod8=mod8*(1/max(mod8));
mod16=(t16.^4).*exp(-90*(t16.^0.5));
mod16=mod16*(1/max(mod16));

f0 = 2*146.8; 

ScaleTable = [2/3 3/4 5/6 15/16 ...
1 9/8 5/4 4/3 3/2 5/3 9/5 15/8 ...
2 9/4 5/2 8/3 3 10/3 15/4 4 ...
1/2 9/16 5/8];

do0f = mod4.*cos(2*pi*ScaleTable(21)*f0*t4);
re0f = mod4.*cos(2*pi*ScaleTable(22)*f0*t4);
mi0f = mod4.*cos(2*pi*ScaleTable(23)*f0*t4);

fa0f = mod4.*cos(2*pi*ScaleTable(1)*f0*t4);
so0f = mod4.*cos(2*pi*ScaleTable(2)*f0*t4);
la0f = mod4.*cos(2*pi*ScaleTable(3)*f0*t4);
ti0f = mod4.*cos(2*pi*ScaleTable(4)*f0*t4);
do1f = mod4.*cos(2*pi*ScaleTable(5)*f0*t4);
re1f = mod4.*cos(2*pi*ScaleTable(6)*f0*t4);
mi1f = mod4.*cos(2*pi*ScaleTable(7)*f0*t4);
fa1f = mod4.*cos(2*pi*ScaleTable(8)*f0*t4);
so1f = mod4.*cos(2*pi*ScaleTable(9)*f0*t4);
la1f = mod4.*cos(2*pi*ScaleTable(10)*f0*t4);
tb1f = mod4.*cos(2*pi*ScaleTable(11)*f0*t4);
ti1f = mod4.*cos(2*pi*ScaleTable(12)*f0*t4);
do2f = mod4.*cos(2*pi*ScaleTable(13)*f0*t4);
re2f = mod4.*cos(2*pi*ScaleTable(14)*f0*t4);
mi2f = mod4.*cos(2*pi*ScaleTable(15)*f0*t4);
fa2f = mod4.*cos(2*pi*ScaleTable(16)*f0*t4);
so2f = mod4.*cos(2*pi*ScaleTable(17)*f0*t4);
la2f = mod4.*cos(2*pi*ScaleTable(18)*f0*t4);
ti2f = mod4.*cos(2*pi*ScaleTable(19)*f0*t4);
do3f = mod4.*cos(2*pi*ScaleTable(20)*f0*t4);
blkf = zeros(1,i);

do0e = mod8.*cos(2*pi*ScaleTable(21)*f0*t8);
re0e = mod8.*cos(2*pi*ScaleTable(22)*f0*t8);
mi0e = mod8.*cos(2*pi*ScaleTable(23)*f0*t8);

fa0e = mod8.*cos(2*pi*ScaleTable(1)*f0*t8);
so0e = mod8.*cos(2*pi*ScaleTable(2)*f0*t8);
la0e = mod8.*cos(2*pi*ScaleTable(3)*f0*t8);
ti0e = mod8.*cos(2*pi*ScaleTable(4)*f0*t8);
do1e = mod8.*cos(2*pi*ScaleTable(5)*f0*t8);
re1e = mod8.*cos(2*pi*ScaleTable(6)*f0*t8);
mi1e = mod8.*cos(2*pi*ScaleTable(7)*f0*t8);
fa1e = mod8.*cos(2*pi*ScaleTable(8)*f0*t8);
so1e = mod8.*cos(2*pi*ScaleTable(9)*f0*t8);
la1e = mod8.*cos(2*pi*ScaleTable(10)*f0*t8);
tb1e = mod8.*cos(2*pi*ScaleTable(11)*f0*t8);
ti1e = mod8.*cos(2*pi*ScaleTable(12)*f0*t8);
do2e = mod8.*cos(2*pi*ScaleTable(13)*f0*t8);
re2e = mod8.*cos(2*pi*ScaleTable(14)*f0*t8);
mi2e = mod8.*cos(2*pi*ScaleTable(15)*f0*t8);
fa2e = mod8.*cos(2*pi*ScaleTable(16)*f0*t8);
so2e = mod8.*cos(2*pi*ScaleTable(17)*f0*t8);
la2e = mod8.*cos(2*pi*ScaleTable(18)*f0*t8);
ti2e = mod8.*cos(2*pi*ScaleTable(19)*f0*t8);
do3e = mod8.*cos(2*pi*ScaleTable(20)*f0*t8);
blke = zeros(1,j);                            

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 沈再阳.精通MATLAB信号处理[M].清华大学出版社，2015.
[2]高宝建,彭进业,王琳,潘建寿.信号与系统——使用MATLAB分析与实现[M].清华大学出版社，2020.
[3]王文光,魏少明,任欣.信号处理与系统分析的MATLAB实现[M].电子工业出版社，2018.
[4]郑炜.基于改进小波阈值的电能质量扰动信号去噪算法[J].电气开关. 2021,59(01)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/122892077