【ELM回归预测】基于matlab粒子群算法优化ELM回归预测【含Matlab源码 1722期】
一、粒子群算法优化极限学习机ELM简介
PSO-ELM优化算法预测模型
ELM模型在训练之前可以随机产生ω和b, 只需要确定隐含层神经元个数及隐含层神经元激活函数, 即可实现ELM预测模型的构建。在ELM模型的构建中, 只需确定初始ω和b, 而无需复杂的参数设置, 具有学习速度快、泛化性能好等优点。然而在发动机参数预测过程中, 不同的参数设置, 对预测模型的准确度起着一定程度的影响。此时, 如果通过简单的随机选取初始化参数方法来构建极限学习机模型, 在一定程度上存在着模型构建中隐含层节点冗余等缺点, 这在一定程度上阻碍了ELM模型的精确性。因此, 在构建EGTM数据预测模型的过程中, 可通过PSO算法寻优确定模型的最佳参数, 以保证ELM模型的准确性。
PSO优化算法于1995年由美国学者Eberhart和Kennedy提出。在优化过程中, 通过跟踪个体最优粒子pmbest与群体最优粒子gmbest, 从而更新粒子的速度与位置:

式中:d表示粒子搜索的空间维数, i为搜索过程中种群规模大小, m为当前种群代数。r∈(0,1), 表示随机数, c∈(0,2), 表示学习因子, 取值由经验设定。ω为惯性权重系数, 用x与v分别表示粒子的当前位置与当前速度, pmbest表示当前个体最优粒子位置, gmbest表示当前群体最优粒子位置。
利用PSO算法的收敛性强、鲁棒性好等优点, 可以在较短的运行时间内, 在保证精确度的情况下有效地寻找全局最优解。PSO-ELM算法的流程如图1所示。
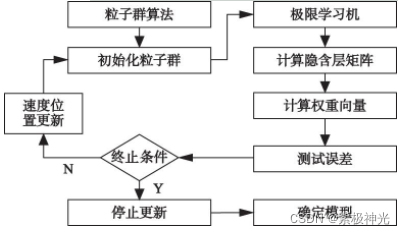
图1 PSO-ELM算法流程图
如图1所示, 在构建ELM预测模型的过程中, 利用PSO算法的参数优化能力, 通过建立适应值函数计算适应值, 以验证PSO算法中粒子的优劣。通过不断更新粒子, 以确保粒子不断趋向于全局最优。在预测过程中, 以预测结果与真实值之间的误差作为适应值函数, 通过寻找使得适应值函数最小的全局最优解, 从而确定更加精确的ELM预测模型, 为构建合理的ELM预测模型提供了理论基础。
二、部分源代码
clc
clear all
%% 遍历和分组
raw = xlsread('gaopin.xlsx');
data = zeros(876,6);
label = zeros(876,1);
for i=1:876
for j=0:5
data(i,j+1) = raw(i+j);
end;
label(i,1) = raw(i+6);
end;
data_train = data(1:793,1:6);
label_train = label(1:793,1);
data_test = data(794:876,1:6);
label_test= label(794:876,1);
%% 载入数据
AllSamIn = data_train';
AllSamOut =label_train';
AllTestIn=data_test';
AllTestOut=label_test';
%% 训练样本归一化
global minAllSamOut;
global maxAllSamOut;
[AllSamInn,minAllSamIn,maxAllSamIn,AllSamOutn,minAllSamOut,maxAllSamOut] = premnmx(AllSamIn,AllSamOut);
TrainSamIn=AllSamInn;
TrainSamOut=AllSamOutn;
global Ptrain;
Ptrain = TrainSamIn;
global Ttrain;
Ttrain = TrainSamOut;
%% 测试样本归一化
global minAllTestOut;
global maxAllTestOut;
[AllTestInn,minAllTestIn,maxAllTestIn,AllTestOutn,minAllTestOut,maxAllTestOut] = premnmx(AllTestIn,AllTestOut);
TestIn=AllTestInn;
TestOut=AllTestOutn;
global Ptest;
Ptest = TestIn;
global Ttest;
Ttest = TestOut;
%% 加载网络的初始变量
global indim;
indim=6;
global hiddennum;
hiddennum=50;
global outdim;
outdim=1;
%% 加载PSO模型的相关参数
vmax=1;
minerr=0.001;
wmax=0.80;
wmin=0.40;
global itmax;
itmax=100;
c1=2.4;
c2=1.6;
for iter=1:itmax
W(iter)=wmax-((wmax-wmin)/itmax)*iter;
end
a=-1;
b=1;
m=-1;
n=1;
global N;
N=100;
global D;
D=(indim+1)*hiddennum+(hiddennum+1)*outdim;
rand('state',sum(100*clock));
X=a+(b-a)*rand(N,D,1);
V=m+(n-m)*rand(N,D,1);
global fvrec;
MinFit=[];
BestFit=[];
%% PSO优化ELM模型 过程 1
fitness=fitcal(X,indim,hiddennum,outdim,D,Ptrain,Ttrain,minAllSamOut,maxAllSamOut);
fvrec(:,1,1)=fitness(:,1,1);
[C,I]=min(fitness(:,1,1));
MinFit=[MinFit C];
BestFit=[BestFit C];
L(:,1,1)=fitness(:,1,1);
B(1,1,1)=C;
gbest(1,:,1)=X(I,:,1);
for p=1:N
G(p,:,1)=gbest(1,:,1);
end
for i=1:N;
pbest(i,:,1)=X(i,:,1);
end
V(:,:,2)=W(1)*V(:,:,1)+c1*rand*(pbest(:,:,1)-X(:,:,1))+c2*rand*(G(:,:,1)-X(:,:,1));
for ni=1:N
for di=1:D
if V(ni,di,2) > vmax
V(ni,di,2) = vmax;
elseif V(ni,di,2) < -vmax
V(ni,di,2) = -vmax;
else
V(ni,di,2) = V(ni,di,2);
end
end
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
三、运行结果
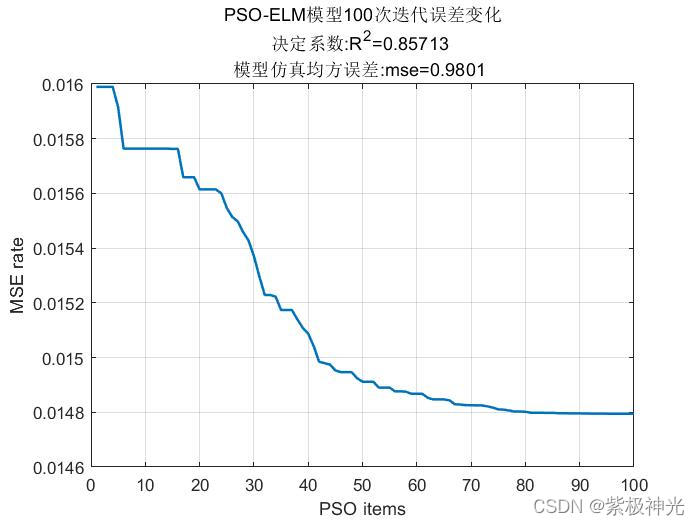
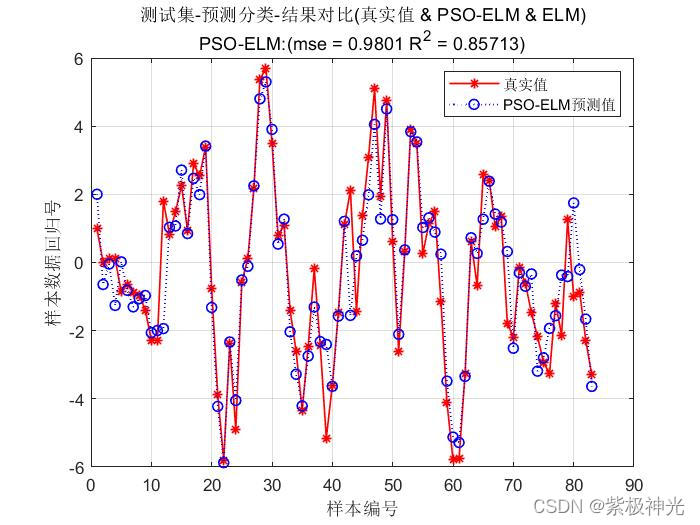
四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社,2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社,2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社,2018.
[6]戴邵武,陈强强,刘志豪,戴洪德.基于粒子群极限学习机的排气温度裕度预测[J].仪表技术. 2019,(06)
文章来源: qq912100926.blog.csdn.net,作者:海神之光,版权归原作者所有,如需转载,请联系作者。
原文链接:qq912100926.blog.csdn.net/article/details/123041225
- 点赞
- 收藏
- 关注作者



评论(0)