【单目标优化求解】基于matlab多阶段动态扰动和动态惯性权重布谷鸟算法求解单目标优化问题【含Matlab源码 1656期】

一、布谷鸟算法简介（具体理论见参考文献[3]）

布谷鸟算法，英文叫做Cuckoo search (CS algorithm)。首先还是同样，介绍一下这个算法的英文含义， Cuckoo是布谷鸟的意思，啥是布谷鸟呢，是一种叫做布谷的鸟，o(∩_∩)o ，这种鸟她妈很懒，自己生蛋自己不养，一般把它的宝宝扔到别的种类鸟的鸟巢去。但是呢，当孵化后，遇到聪明的鸟妈妈，一看就知道不是亲生的，直接就被鸟妈妈给杀了。于是这群布谷鸟宝宝为了保命，它们就模仿别的种类的鸟叫，让智商或者情商极低的鸟妈妈误认为是自己的亲宝宝，这样它就活下来了。
布谷鸟搜索算法（Cuckoo Search, CS）是2009年Xin-She Yang 与Suash Deb在《Cuckoo Search via Levy Flights》一文中提出的一种优化算法。布谷鸟算法是一种集合了布谷鸟巢寄生性和莱维飞行（Levy Flights）模式的群体智能搜索技术，通过随机游走的方式搜索得到一个最优的鸟巢来孵化自己的鸟蛋。这种方式可以达到一种高效的寻优模式。

1 布谷鸟的巢寄生性

2 莱维飞行

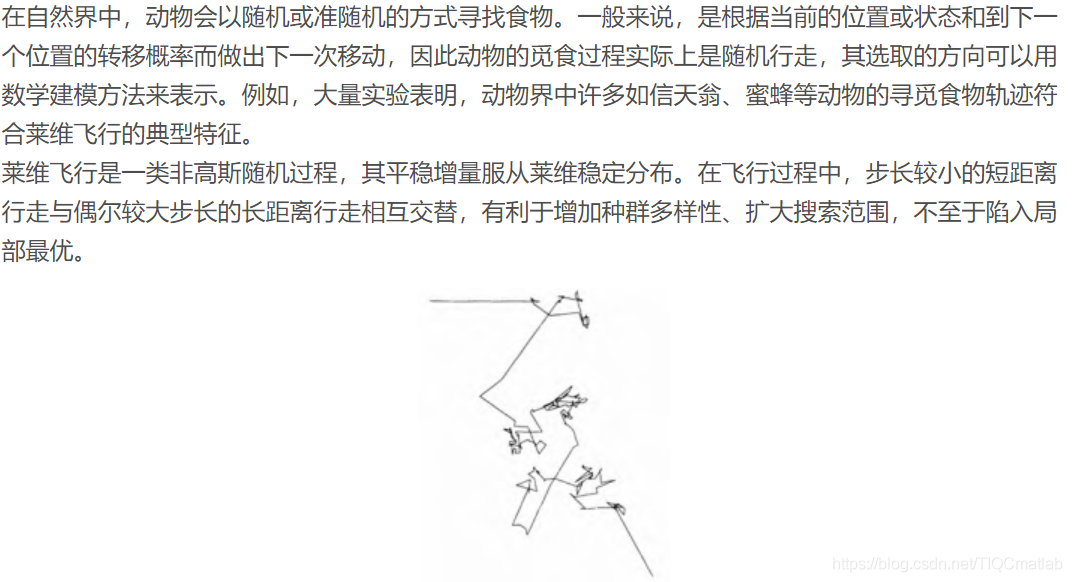
图1.模拟莱维飞行轨迹示意图

3 布谷鸟搜索算法的实现过程

二、部分源代码

%% 清除环境变量
clear 
clc

%% 参数设置
N = 25;             % 种群规模
Function_name = 'F1';         % 从F1到F23的测试函数的名称（本文中的表1、2、3）
Max_iteration = 1000;           % 最大迭代次数
cnt_max = 30;
% 加载所选基准函数的详细信息
[lb, ub, dim, fobj] = Get_Functions_details(Function_name);

Curve_MACS = zeros(1, Max_iteration);
Curve_CS = zeros(1, Max_iteration);
Curve_BA = zeros(1, Max_iteration);
Curve_FPA = zeros(1, Max_iteration);
Curve_ASCSA = zeros(1, Max_iteration);

for cnt = 1:cnt_max
    % 初始化种群位置
    X = initialization(N, dim, ub, lb);
    
    [MACS_Best_score(cnt), MACS_Best_pos(cnt, :), MACS_Curve] = MACS(X, N, Max_iteration, lb, ub, dim, fobj);
    [CS_Best_score(cnt), CS_Best_pos(cnt, :), CS_Curve] = CS(X, N, Max_iteration, lb, ub, dim, fobj);
    [BA_Best_score(cnt), BA_Best_pos(cnt, :), BA_Curve] = BA(X, N, Max_iteration, lb, ub, dim, fobj);
    [FPA_Best_score(cnt), FPA_Best_pos(cnt, :), FPA_Curve] = FPA(X, N, Max_iteration, lb, ub, dim, fobj);
    [ASCSA_Best_score(cnt), ASCSA_Best_pos(cnt, :), ASCSA_Curve] = ASCSA(X, N, Max_iteration, lb, ub, dim, fobj);
    
    Curve_MACS = Curve_MACS+MACS_Curve;
    Curve_CS = Curve_CS+CS_Curve;
    Curve_BA = Curve_BA+BA_Curve;
    Curve_FPA = Curve_FPA+FPA_Curve;
    Curve_ASCSA = Curve_ASCSA+ASCSA_Curve;
end


Curve_MACS = Curve_MACS/cnt_max;
Curve_CS = Curve_CS/cnt_max;
Curve_BA = Curve_BA/cnt_max;
Curve_FPA = Curve_FPA/cnt_max;
Curve_ASCSA = Curve_ASCSA/cnt_max;

std_MACS = std(MACS_Best_score);
std_CS = std(CS_Best_score);
std_BA = std(BA_Best_score);
std_FPA = std(FPA_Best_score);
std_ASCSA = std(ASCSA_Best_score);

best_MACS = max(MACS_Best_score);
best_CS = max(CS_Best_score);
best_BA = max(BA_Best_score);
best_FPA = max(FPA_Best_score);
best_ASCSA = max(ASCSA_Best_score);

worst_MACS = min(MACS_Best_score);
worst_CS = min(CS_Best_score);
worst_BA = min(BA_Best_score);
worst_FPA = min(FPA_Best_score);
worst_ASCSA = min(ASCSA_Best_score);

mean_MACS = mean(MACS_Best_score);
mean_CS = mean(CS_Best_score);
mean_BA = mean(BA_Best_score);
mean_FPA = mean(FPA_Best_score);
mean_ASCSA = mean(ASCSA_Best_score);

%% 画图
% 1、画出所选基准函数的三维立体图形
figure;
func_plot(Function_name);
title(Function_name)
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
img =gcf;  %获取当前画图的句柄
print(img, '-dpng', '-r600', './img4.png')         %即可得到对应格式和期望dpi的图像
% 2、画出目标函数值变化曲线图
figure;
t = 1:Max_iteration;
semilogy(t, Curve_MACS, 'rd-',  t, Curve_CS, 'go-', t, Curve_BA, 'bs-',  t, Curve_FPA, 'mv-', t, Curve_ASCSA, 'k^-', ...
    'linewidth', 1.5, 'MarkerSize', 8, 'MarkerIndices', 1:50:Max_iteration);
legend('MACS', 'CS', 'BA', 'FPA', 'ASCSA');
% title(Function_name)
xlabel('Iteration');
ylabel('Fitness');
axis fill
grid on
box on
img =gcf;  %获取当前画图的句柄
print(img, '-dpng', '-r600', './img3.png')         %即可得到对应格式和期望dpi的图像
%% 显示结果
disp(['函数：', num2str(Function_name)]);
disp(['MACS：最大值: ', num2str(best_MACS), ',最小值:', num2str(worst_MACS), ',平均值:', num2str(mean_MACS), ',标准差:', num2str(std_MACS)]);
disp(['CS：最大值: ', num2str(best_CS), ',最小值:', num2str(worst_CS), ',平均值:', num2str(mean_CS), ',标准差:', num2str(std_CS)]);
disp(['BA：最大值: ', num2str(best_BA), ',最小值:', num2str(worst_BA), ',平均值:', num2str(mean_BA), ',标准差:', num2str(std_BA)]);
disp(['FPA：最大值: ', num2str(best_FPA), ',最小值:', num2str(worst_FPA), ',平均值:', num2str(mean_FPA), ',标准差:', num2str(std_FPA)]);
disp(['ASCSA：最大值: ', num2str(best_ASCSA), ',最小值:', num2str(worst_ASCSA), ',平均值:', num2str(mean_ASCSA), ',标准差:', num2str(std_ASCSA)]);

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
 

三、运行结果

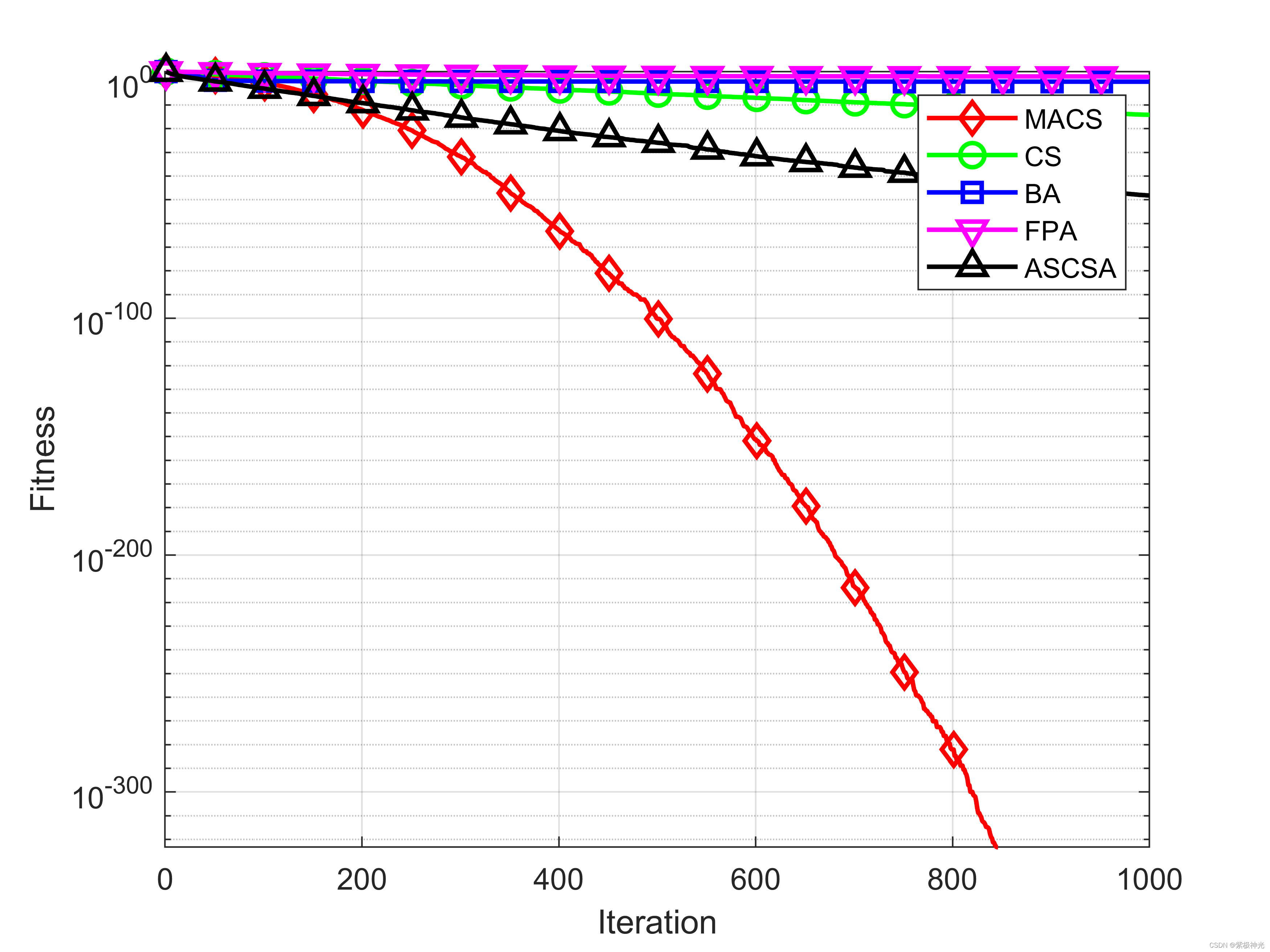
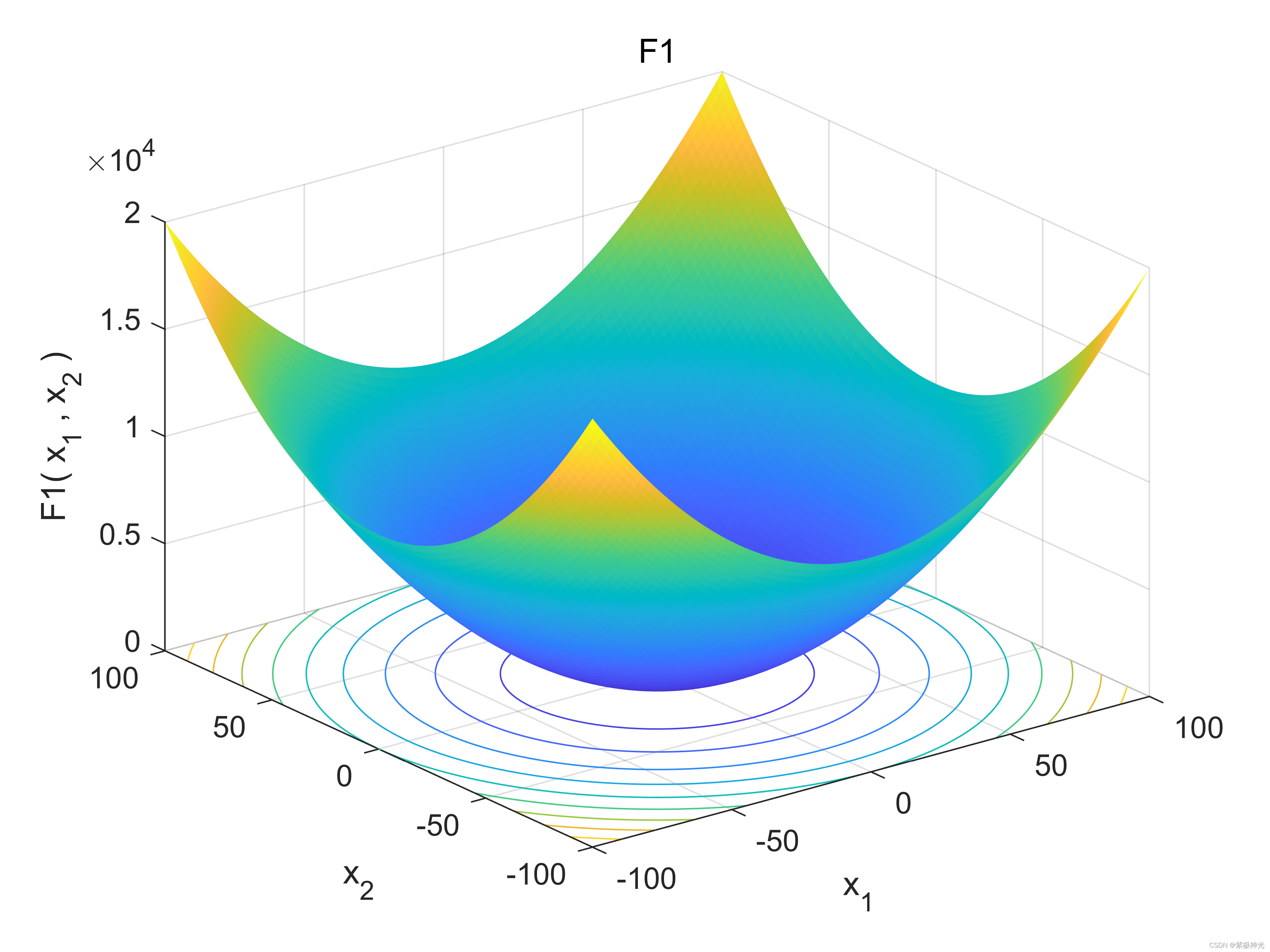
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]张珍珍,贺兴时,于青林,杨新社.多阶段动态扰动和动态惯性权重的布谷鸟算法[J].计算机工程与应用

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/122500734