【故障诊断分析】基于matlab小波变换外圈轴承故障诊断【含Matlab源码 1678期】

一、简介

在滚动轴承的故障诊断时，传统的频谱分析法通常采用共振解调技术 ， 具有良好的效果 ，但当内圈 、 滚动体或多点故障时，解调谱线却很难分辨故障类型小波包是小波理论在信号处理应用领域的又一重大发展，它在小波理论的基础上引人了最优基准准则，目前已在通信、 图像处理、分形 、信号检测等方面获得成功应用小波包分解是多分辨率分析的推广，是一种比小波分析更为精细的信号时频分析方法 ，它将频带进行多层次划分 ， 对小波分析没有细分的高频部分也进行了分解，并能根据被分析信号的特征 ， 自适应地 选择频带，使之与信号频谱相匹配 ，从而提高时频分辨率， 因此它是一种非常有效的信号处理方法。本文将用小波包分析方法构造滚动轴承状态检测信号的能量特征向量，再用神经网络方法对滚动轴承的状态进行识别。

1 小波包理论



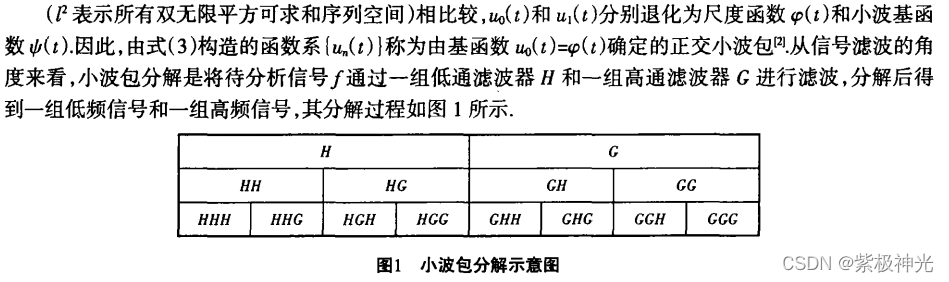
2 特征频率估算
滚动轴承各部件发生单点故障时 ， 其特征信号频率为

3 构造能量特征向量
当轴承在负载旋转过程中出现疲劳 、 压痕或局部腐蚀等故障时 ， 将产生冲击振动 ， 而这些振动反复互激又会引起更大的振颤 ， 用加速度传感器获取运动中轴承的振动加速度信号 ， 由于轴承的故障使得该振动信号在某些频带内的信号能量减小 ， 而使另外一些频带内的信号能量增强 ， 因此 ， 在各频率成分信号的能量中， 包含了丰富的故障信息 ，某种或某几种频率成分能量 的改变代表一种故障，基于这点，由轴承振动信号的各频段能量相对值构造轴承故障特征向量。

二、部分源代码

clear all
clc

load 10k_32768_5.dat
s=X10k_32768_5';

fs=10000;                                                 %采样频率
N=32768;                                                  %采样点数


[c,l]=wavedec(s,11,'haar');  %11层分解
ca1=appcoef(c,l,'haar',1);   %V10
ca2=appcoef(c,l,'haar',2);   %V9
ca3=appcoef(c,l,'haar',3);   %V8
ca4=appcoef(c,l,'haar',4);   %V7
ca5=appcoef(c,l,'haar',5);   %V6
ca6=appcoef(c,l,'haar',6);   %V5
ca7=appcoef(c,l,'haar',7);   %V4
ca8=appcoef(c,l,'haar',8);   %V3
ca9=appcoef(c,l,'haar',9);   %V2
ca10=appcoef(c,l,'haar',10);   %V1
ca11=appcoef(c,l,'haar',11);   %V0

cd1=detcoef(c,l,1);   %W10
cd2=detcoef(c,l,2);   %W9
cd3=detcoef(c,l,3);   %W8
cd4=detcoef(c,l,4);   %W7
cd5=detcoef(c,l,5);   %W6
cd6=detcoef(c,l,6);   %W5
cd7=detcoef(c,l,7);   %W4
cd8=detcoef(c,l,8);   %W3
cd9=detcoef(c,l,9);   %W2
cd10=detcoef(c,l,10);   %W1
cd11=detcoef(c,l,11);   %W0

%消噪，将高频成分中小于阈值的数置零，规则自行改变

figure(2);
subplot(5,1,1);plot(ca1);ylabel('V10');title('第一层近似系数')
subplot(5,1,2);plot(ca2);ylabel('V9');title('第二层近似系数')
subplot(5,1,3);plot(ca3);ylabel('V8');title('第三层近似系数')
subplot(5,1,4);plot(ca4);ylabel('V7');title('第四层近似系数')
subplot(5,1,5);plot(ca5);ylabel('V6');title('第五层近似系数')

figure(3);
subplot(6,1,1);plot(ca6);ylabel('V5');title('第六层近似系数')
subplot(6,1,2);plot(ca7);ylabel('V4');title('第七层近似系数')
subplot(6,1,3);plot(ca8);ylabel('V3');title('第八层近似系数')
subplot(6,1,4);plot(ca9);ylabel('V2');title('第九层近似系数')
subplot(6,1,5);plot(ca10);ylabel('V1');title('第十层近似系数')
subplot(6,1,6);plot(ca11);ylabel('V0');title('第十一层近似系数')

figure(4);
subplot(6,1,1);plot(cd1);ylabel('W10');title('第一层小波细节系数')%细节系数
subplot(6,1,2);plot(cd2);ylabel('W9');title('第二层小波细节系数')
subplot(6,1,3);plot(cd3);ylabel('W8');title('第三层小波细节系数')
subplot(6,1,4);plot(cd4);ylabel('W7');title('第四层小波细节系数')
subplot(6,1,5);plot(cd5);ylabel('W6');title('第五层小波细节系数')
subplot(6,1,6);plot(cd6);ylabel('W5');title('第六层小波细节系数')
figure(5);
subplot(5,1,1);plot(cd7);ylabel('W4');title('第七层小波细节系数')
subplot(5,1,2);plot(cd8);ylabel('W3');title('第八层小波细节系数')
subplot(5,1,3);plot(cd9);ylabel('W2');title('第九层小波细节系数')
subplot(5,1,4);plot(cd10);ylabel('W1');title('第十层小波细节系数')
subplot(5,1,5);plot(cd11);ylabel('W0');title('第十一层小波细节系数')

figure(6)
subplot(2,1,1);plot(s_rec);xlim([0 N]);title('进行小波分解后重组信号时域图')
axis([0,15000,0,0.22]);
subplot(2,1,2);plot(0:2*fs/N:2*(N/2-1)*fs/N,f_rec(1:N/2));title('外圈故障小波分解重组信号FFT频谱图')
axis([0,1000,0,0.005]);


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
 

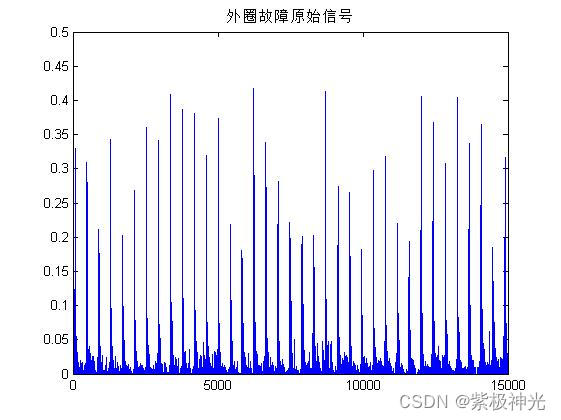
三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 沈再阳.精通MATLAB信号处理[M].清华大学出版社，2015.
[2]高宝建,彭进业,王琳,潘建寿.信号与系统——使用MATLAB分析与实现[M].清华大学出版社，2020.
[3]王文光,魏少明,任欣.信号处理与系统分析的MATLAB实现[M].电子工业出版社，2018.
[4]张国新,刘祚时.基于小波包分析的滚动轴承故障诊断[J].江西理工大学学报. 2007,(01)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/122540056