【优化算法】Iterative映射和单纯形法的改进灰狼优化算法(SMIGWO)【含Matlab源码 1746期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【优化算法】Iterative映射和单纯形法的改进灰狼优化算法(SMIGWO)【含Matlab源码 1746期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、SMIGWO简介

为了解决基本灰狼优化算法（GWO）依赖初始种群和求解精度不高的问题,提出一种基于Iterative映射和单纯形法的改进灰狼优化算法（SMIGWO）。该算法利用混沌Iterative映射产生初始灰狼种群,增强全局搜索过程中的种群多样性;采用逆不完全Γ函数更新收敛因子,以平衡算法的全局搜索和局部搜索能力;利用单纯形法的反射、扩张和收缩操作对当前较差个体进行改进,避免算法陷入局部最优。

1 改进的灰狼优化算法
1.1 混沌序列初始化
基本GWO算法在搜索空间中随机初始化灰狼种群, 容易造成灰狼位置分布不均匀, 导致种群多样性差。混沌映射具有较好的遍历性和不重复性, 因此可以用来代替种群随机初始化。文中采用Iterative混沌映射产生灰狼的初始位置, Iterative映射的数学表达式为:

其中, b是控制参数, b∈ (0, 1) , 文中取b=0.5。

1.2 基于逆不完全Γ函数的收敛因子
当|A|>1时, 灰狼群体将扩大搜索范围寻找猎物, 即全局搜索, 收敛速度快;当|A|<1时, 灰狼群体将收缩搜索范围对猎物进行攻击, 即局部搜索, 收敛速度慢。因此, A的大小与GWO算法的全局搜索和局部搜索能力有很大关系。由式 (3) 可以看出, A随着收敛因子a的变化而变化。为了平衡算法的全局搜索和局部搜索能力, 文中提出一种基于逆不完全Γ函数的收敛因子:

其中:amax、amin为收敛因子a的最大、最小值, t为当前迭代次数, tmax为最大迭代次数, λ (λ≥0) 是随机变量, 本文取λ=0.01。图2是a的变化趋势图。

从图2可以看出, 收敛因子a随着迭代次数从2非线性递减到0, 迭代初期接近线性下降, 而在迭代后期接近指数下降, 能较好地实现探索与开发之间的平衡。

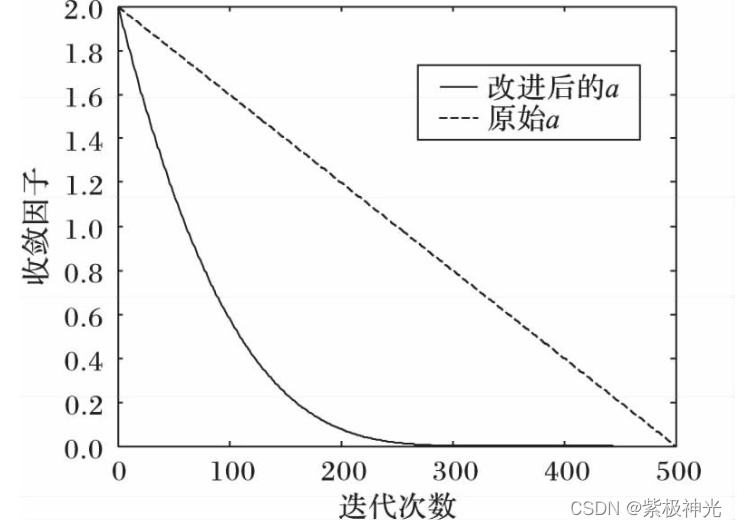
图2 收敛因子改进前后对比

1.3 单纯形法
单纯形法的核心思想包括两重:一是梯度估计, 它是从最差顶点Xs到除最差顶点Xs以外的所有顶点的质心X的方向向量g;二是通过迭代用一个更好的新顶点来代替最差顶点。新的顶点是由4种算子之一产生的:反射、扩张、外收缩和内收缩[15]。如图3所示, Xc是最优点Xg和次优点Xb的中心, 假设Xs是较差点。

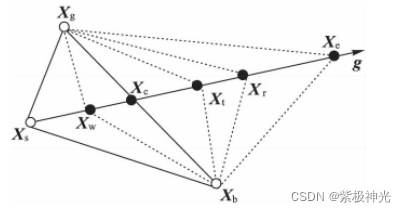
图3 单纯形法的四种运算
反射操作:Xr=Xc+α (Xc-Xs) , Xr是反射点, 反射系数α通常取1。
扩张操作:Xe=Xc+γ (Xr-Xc) , Xe是扩张点, 扩张系数γ通常取2。
外收缩操作:Xt=Xc+β (Xs-Xc) , Xt是外收缩点, 外收缩系数β取0.5。
内收缩操作:Xw=Xc-β (Xs-Xc) , Xw是内收缩点, 内收缩系数β取0.5。

1.4 改进的灰狼优化算法的执行步骤
综合以上策略描述, 给出SMIGWO的具体步骤:

1. 设置算法参数:种群规模N, 最大迭代次数tmax, 反射系数α, 扩张系数γ, 内、外收缩系数β, 随机生成a、A、C等参数;
2. 利用混沌Iterative映射初始化灰狼种群;
3. 计算种群中每个灰狼个体的适应度值, 并按照适应度值进行排序, 选择前3个最好的狼, 记录位置Xα、Xβ和Xδ, 对应的适应度值f (Xα) 、f (Xβ) 和f (Xδ) , 中心位置为Xc= (Xα+Xβ) /2。
4. 对较差灰狼位置Xs进行反射, 得到反射点Xr。
5. 若f (Xr) <f (Xα) 说明反射方向正确, 执行扩张操作得到扩张点Xe, 若f (Xe) <f (Xα) , 则用Xe取代Xs;否则, 用Xr取代Xs。
6. 若f (Xr) >f (Xs) , 说明反射方向不正确, 执行外收缩操作得到外收缩点Xt, 若f (Xt) <f (Xs) , 则用Xt取代Xs。
7. 若f (Xα) <f (Xr) <f (Xs) , 执行内收缩操作得到内收缩点Xw, 若f (Xw) <f (Xs) , 则用Xw取代Xs;否则, 用Xt取代Xs。
8. 利用式 (5) 和 (6) 更新种群中其他X灰狼个体的位置;
9. 利用式 (8) 计算a, 然后利用式 (3) 和 (4) 更新A, C的值;
10. 判断算法是否满足结束条件, 若满足, 则算法结束, 输出最优灰狼位置Xα;否则, 执行步骤3) 。

1.5 算法收敛性分析
算法优化的初始步骤中, 灰狼种群移动应该有较大的变化, 这有助于广泛地探索搜索空间, 然后, 应该减少这些变化, 以保证在算法结束时能够在最优解附近收敛。SMIGWO使用混沌映射策略和单纯形法, 使狼群初期探索更具随机性, 采用基本的GWO算法更新策略更新其他X灰狼的位置,SMIGWO最终可以收敛到搜索空间中的某一点。

三、部分源代码

 %% [1]王梦娜,王秋萍,
 王晓峰.基于Iterative映射和单纯形法的改进灰狼优化算法[J].计算机应用,2018,38(S2):16-20+54.
%该方法改进效果不咋样
clear all 
clc
SearchAgents_no=30; %种群数量
Function_name='F1'; % CEC2005 测试函数F1-F21

Max_iteration=1000; % 最大迭代次数

% 获取对应测试函数的边界信息，维度等。
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
%基础灰狼算法
[Best_score,Best_pos,GWO_cg_curve]=GWO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
%改进灰狼算法
[Best_score1,Best_pos1,GWO_cg_curve1]=SMIGWO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);

figure('Position',[500 500 660 290])
%Draw search space
subplot(1,2,1);
func_plot(Function_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])

%Draw objective space
subplot(1,2,2);
semilogy(GWO_cg_curve,'Color','b','linewidth',1.5)
hold on
semilogy(GWO_cg_curve1,'Color','r','linewidth',1.5);
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');
axis tight
grid on
box on
legend('GWO','SMIGWO');

display(['The best solution obtained by GWO is : ', num2str(Best_pos)]);
display(['The best optimal value of the objective funciton found by GWO is : ', num2str(Best_score)]);

        
display(['The best solution obtained by SMIGWO is : ', num2str(Best_pos1)]);
display(['The best optimal value of the objective funciton found by SMIGWO is : ', num2str(Best_score1)]);


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
 

三、运行结果

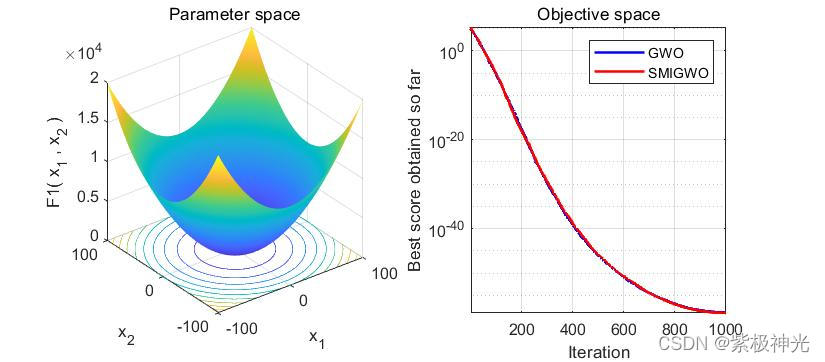
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]王梦娜,王秋萍,王晓峰.基于Iterative映射和单纯形法的改进灰狼优化算法[J].计算机应用. 2018,38(S2)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/123155263