【BP时间序列预测】基于matlab EMD优化BP神经网络汇率预测【含Matlab源码 1742期】

一、EMD优化BP神经网络简介

1 经验模态分解算法
基于经验模态分解(empirical mode decomposition, EMD)的分析方法较多运用于非线性、非平稳信号的分析。在短时交通流预测中，将非线性、非平稳的交通流信号转化为线性、平稳的交通流信号更能反映其物理意义。由于实质是通过特征时间尺度来识别交通流信号中所含的所有振动模态，与其他信号处理方法相比，经验模态分解方法具有直观、间接、自适应等特点。EMD分解方法基于以下假设条件：

1. 数据至少有2个极值、1个最大值和1个最小值；若没有极值点，只有拐点，再对数据求1次或多次微分便可以得到极值。

2. 极值点间的时间尺度唯一决定交通流信号随时间变化的趋势。

经EMD处理后的原始交通流信号可根据其自身特点自适应分解为有限个经验模态分量(IMF)和残余量(RES),使原始交通流信号不同时间尺度的局部特征信号包含在各个分量中，进而使非平稳数据平稳化。其中每个IMF须同时满足2个条件[17]:① 在整个时间范围内，函数具有相同数目的局部极值点和过零点，或两者最多相差1个；② 由局部最大值形成的上包络线和局部最小值形成的下包络线的平均值必须为0。其分解过程如下：

步骤1 首先求原始交通流信号X(t)的所有极值点，并用3次样条插值函数拟合出原始交通流信号的上、下包络线e1(t)、e2(t),计算上、下包络线的平均值e(t):

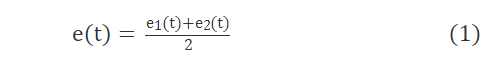
将原信号X(t)与包络线平均值e(t)作差，得到c(t):

步骤2 判断c(t)是否满足IMF的条件，如果满足，将c(t)作为第1个IMF,记为f1(t);如果不满足，则把c(t)当作新的原始交通流信号，重复步骤1,至满足IMF为止。

步骤3 将f1(t)从X(t)中分离出来，再把残余量RESn(t)=X(t)-f1(t)作为新的原始交通流信号，重复上述步骤得到n个IMF,直到X(t)变成一个单调函数时，停止分解，将得到的n个IMF和1个残余量RESn(t)叠加为原始交通流信号X(t):

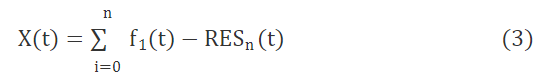
短时交通流受各种因素的干扰，如自身因素和未知的外界因素，各个因素对交通流的趋势变化起着不同的影响因素，因而交通流是一种典型的非平稳信号。利用EMD分解交通流之后，所得的各分量不仅趋于平稳化，且各个分量更能体现交通流的本性和特质。

2 基于BPNN的预测模型
典型的BPNN是由输入层、隐藏层和输出层组成,其中输入层和隐含层之间通过权值连接，隐含层和输出层则通过阈值相连，其输入层包含n个节点，中间层包含m个节点，输出层为1个节点。在预测过程中，基本执行过程是由输入信息的正向传播和误差的逆向传播2个过程组成，如图1和图2所示。

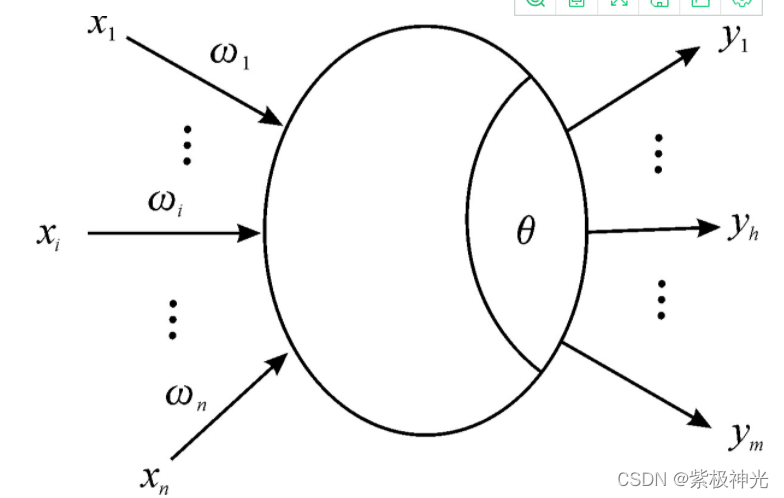
图1 单神经元结构示意图

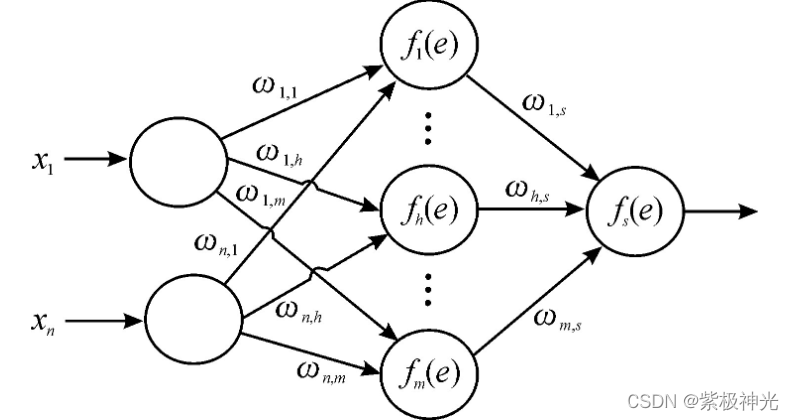
图2 神经网络结构示意图
每个神经模型的激活函数为：

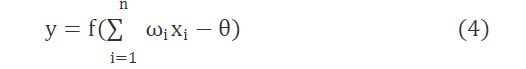
其中： θ为阈值；权值ωi的范围为[-1,1];n为输入层神经元数；y为输出层。激活函数为：

神经元训练是反复迭代的过程。使用来自训练数据集的新数据修改权重，误差的总和定义为：

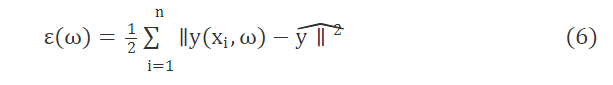
其中yˆ为期望输出值。

模型通过调整权重来减少误差，调整权重的等式为：

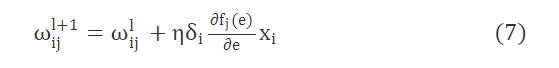
其中： η 为学习率；l为迭代次数； ωlij是神经元i和神经元j之间的权重值；∂fj(e)∂e为神经元j的神经激活函数的导数；δi(δi=yi−yˆi)是神经元i的输出值和期望值之间的差值。

传统的BPNN学习算法采用梯度下降法。首先，对神经网络的权值和阈值进行随机初始化，然后利用一部分样本数据进行神经网络模型的训练，以网络输出值与实际值之间的均方误差为标准来调整网络的权值和阈值，当达到设定的误差标准时，即完成网络的训练过程，得到神经网络的初始权值和阈值。该算法的缺点是初始权值和阈值易导致训练结果陷入局部极小值而不是全局最优值，使得网络的预测精度达不到很高的水平。针对该问题，引入差分进化算法对BPNN的参数进行优化，该算法收敛速度快且易实现，能够弥补采用神经网络模型预测短时交通流的不足，提高交通流预测的精度。

二、部分源代码

clc;close all;clear
%%
bp=load('bp.mat');
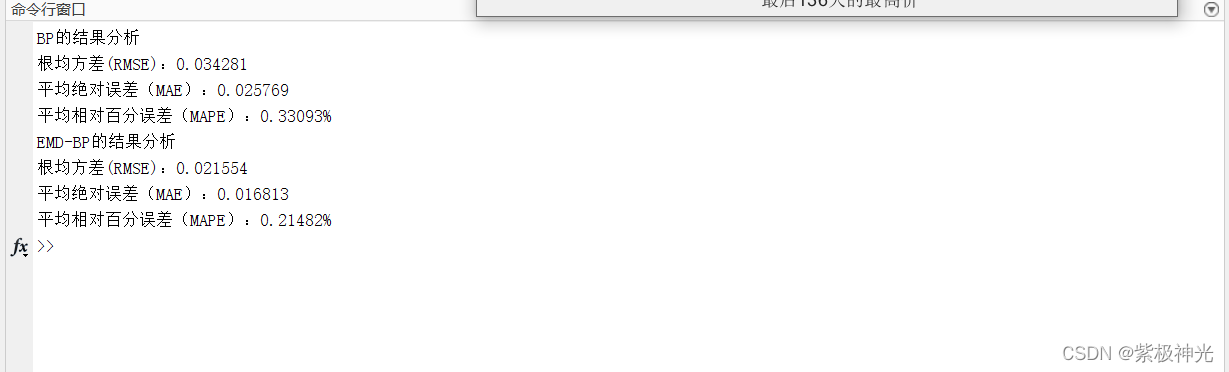
disp('BP的结果分析')
rmse=sqrt(mean((bp.true_value-bp.predict_value).^2));
disp(['根均方差(RMSE)：',num2str(rmse)])

mae=mean(abs(bp.true_value-bp.predict_value));
disp(['平均绝对误差（MAE）：',num2str(mae)])

mape=mean(abs(bp.true_value-bp.predict_value)/bp.true_value);
disp(['平均相对百分误差（MAPE）：',num2str(mape*100),'%'])

%%
emdbp=load('emd_bp.mat');
disp('EMD-BP的结果分析')
rmse=sqrt(mean((emdbp.true_sum-emdbp.predict_sum).^2));
disp(['根均方差(RMSE)：',num2str(rmse)])

mae=mean(abs(emdbp.true_sum-emdbp.predict_sum));
disp(['平均绝对误差（MAE）：',num2str(mae)])

mape=mean(abs(emdbp.true_sum-emdbp.predict_sum)/emdbp.true_sum);
disp(['平均相对百分误差（MAPE）：',num2str(mape*100),'%'])



figure
plot(bp.true_value,'-*','linewidth',3)
hold on
plot(bp.predict_value,'-s','linewidth',3)
plot(emdbp.predict_sum,'-p','linewidth',3)
legend('实际值','BP预测值','EMD-BP预测值')
grid on
ylabel('汇率最高价')
xlabel('最后136天的最高价')
title('BP VS EMD-BP')


  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
 

三、运行结果

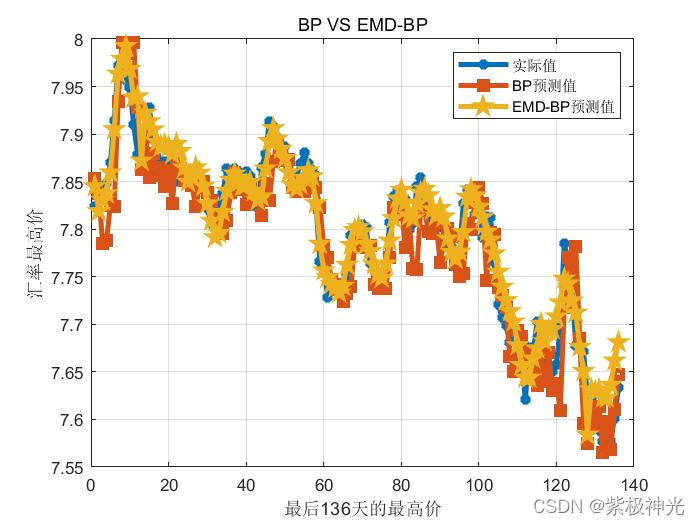
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.
[6]吴玲玲,尹莉莉,任其亮.一种EMD和DE-BPNN组合优化的短时交通流预测方法[M].重庆理工大学学报(自然科学). 2021,35(12)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/123154863