【定位问题】基于matlab RSSI和模拟退火优化粒子群算法求解无线传感器网络定位问题【含Matlab源码 1766期】

一、简介

1 引言
随着物联网技术的发展,传感器之间通过通信方式连接在一起,构成了极为庞大的无线传感器网络,这使得传感器在各行各业的应用相当广泛[。然而,因为大规模抛撒的传感器节点无法全部配备价格昂贵的GPS定位系统,所以不能对全部传感器节点实现精确定位。因此,实现传感器节点的精确定位是无线传感器网络技术中最为关注的问题。

通常,无线传感网络中主要有与距离有关和与距离无关两类定位算法。其中,与距离有关的定位算法主要有TOA算法、TDOA[6]算法和三边定位算法等;与距离无关的定位算法主要有质心定位算法、APIT算法、DV-Hop算法和MDS-MAP算法等。然而,当前定位算法在定位精度方面和实际应用方面还存在一定的不足,为了进一步提高传感器网络的定位精度,国内外研究者进行了更深入的研究工作。在国外,Bulusu等利用传感器网络的连通性,获取了未知节点周边的参考节点并将其作为邻居节点,然后将邻居节点形成的质心作为未知节点的近似位置。Sretenovi等将城市环境下的RSSI模型数据应用到加权质心定位算法中,实现了传感器节点的位置确定,实验结果表明该方法更有实用价值。Sai等在RSSI的基础上提出了并行萤火虫算法,并通过改进目标函数将定位问题转化为非线性无约束问题,结果表明该算法具有更高的定位精度。Mass-Sanchez等采用粒子群算法对DV-hop定位算法进行了优化,获得了比加权DV-hop和双曲线DV-hop方法更好的定位精度。在国内,李腾宇等在基于RSSI加权质心定位算法测出的未知节点到参考节点距离的数学模型上用GASA算法优化求解,其具有更高的定位精度。谢国民等在质心定位算法的基础上,采用PSO-GSA算法对相关参数和位置信息进行优化,有效提高了复杂的煤矿环境中人员的定位精度。张兢等在基于RSSI的加权质心定位的基础上,将已被定位的未知节点作为参考节点再对其他未知节点进行定位,该方法可以有效减少网络连通度较低时不能定位的节点数量。汪晨等采用根据信号识别强度大小获得的距离和参考节点的位置信息作为人工鱼群算法的适应度函数,并对质心定位算法的定位过程进行了寻优求解,提高了定位精度,但大幅增加了计算量。

针对当前质心定位算法中存在的定位精度达不到实际应用要求、计算量较大、成本过高等问题,文中结合群智能算法较好的寻优性能和RSSI质心定位算法计算简单的优点,提出了基于粒子群-模拟退火优化算法-RSSI(Particle Swarm Optimization,Simulated Annealing algorithm and RSSI,PSO-SA-RSSI)的质心定位算法。为了评估本文算法在定位精度等方面的性能,以传统的质心定位算法、基于RSSI的加权质心定位算法和基于粒子群算法优化和RSSI(Particle Swarm Optimization and RSSI,PSO-RSSI)的质心定位算法为对比进行仿真。实验结果表明:本文方法不仅具有较高的定位精度,而且具有计算简单、泛化性能较强等突出的优点。

2 质心定位算法
2.1 无线电信号传播损耗模型
无线电信号传播损耗模型在无线传感器网络定位技术中是最为常用的一种模型。自由空间传播模型的通信区域是以发射节点为原点的圆,在通信区域内的接收节点才能接收到信号,否则无法进行数据交换。在理想环境下,该模型中传感器接收端节点测得的信号接收强度指示值Pr和接收端到发射端之间的距离d满足式(1):

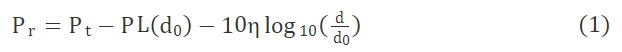
但在实际应用中,无线电信号传输时会受到很多因素的影响,如传输距离、物体反射、折射和散射等。在自由空间模型中对数路径损耗模型加入高斯分布因子能够使其更好地模拟无线电信号在实际环境中的传播过程,因此将其作为本次实验的无线电信号传播损耗模型,具体可描述为:

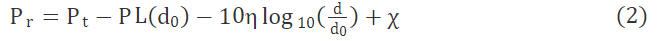
其中,χ代表高斯分布因子;Pr代表接收节点收到信号的功率;Pt代表发射节点发出信号的功率;PL(d0)代表参考距离为d0时的路径损耗功率;η代表路径损耗指数;d代表接收节点和发射节点之间的距离;d0代表距离地面的参考高度,通常取1 m。

2.2 基于RSSI的加权质心定位算法
传统的质心定位算法主要是根据传感器间的连通性,将距离未知节点较近的邻居节点构成多边形,并以该多边形的质心作为定位系统中未知节点的坐标,然而其定位精度较差、实际应用价值不高。为了提高定位算法的定位精度,一些研究者提出了基于RSSI的加权质心定位算法,通过引入RSSI无线电信号传播损耗模型,可以在各个传感器节点传送数据帧时得到未知节点到参考节点的距离,并将该距离作为定位未知节点的权值,以此提高定位的精度。

假设未知节点附近的参考节点的坐标分别为(x1,y1),(x2,y2),…,(xi,yi),…,(xn,yn),传统质心定位的未知节点的坐标为:

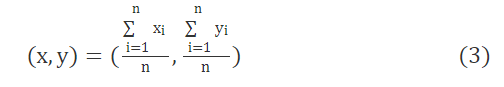
与传统质心定位算法相比,加权质心定位算法只选取距离未知节点最近的3个参考节点A,B和C构成一个围绕未知节点的三角形,通过三角形的质心确定未知节点的位置。假设未知节点到A,B和C 3个参考节点之间的距离分别记为dA,dB和dC,则未知节点的位置坐标为:

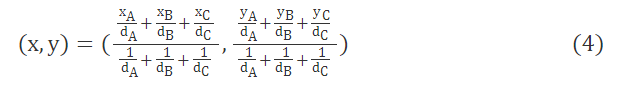
需要注意的是,当距离未知节点最近的参考节点不足3个时,定位过程无法完成。为了解决这一问题,在实际定位过程中将已定位的未知节点作为伪参考节点参与到定位过程中,使得在通信范围内不足3个参考节点的未知节点也能实现精确定位。

3 PSO-SA优化的RSSI质心定位算法
群智能算法作为一种优化算法在各个领域均有应用,其中粒子群算法和模拟退火算法是当前群智能算法研究领域的热点。粒子群算法具有参数少、求解简单、全局搜索能力较强的优点。模拟退火算法是根据热力学中物体受热溶化后重新凝固以达到物体内能最小的过程提出的一种算法,该算法运行效率较高,求解过程不受初始条件的影响,能够用于求解大规模组合优化问题。本文提出了一种混合群智能算法,即粒子群算法结合模拟退火算法优化的RSSI质心定位算法,该算法不仅能够保持粒子群算法操作简单、易于实现的优点,根据模拟退火算法的概率性搜索策略还能改善粒子群算法容易陷入局部极值点的情况,减少算法的运行时间,提高算法的精确度。

3.1 适应度函数
利用粒子群结合模拟退火算法实现精确定位未知节点坐标的本质是:对适应度函数进行多次循环迭代求解出适应度函数的最小值,以准确确定未知节点的位置坐标。因此在对基于RSSI的质心定位算法进行优化求解的过程中,构造合理的适应度函数对于确定未知节点位置坐标极为重要。假设选取距离未知节点最近的3个节点A(xA,yA),B(xB,yB)和C(xC,yC)为邻居节点,其与未知节点之间的距离分别记为:

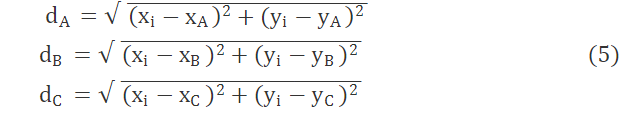
利用参考节点A,B和C到未知节点之间的距离(dA,dB和dC)和基于RSSI模型测距方法(见式(2))得到的距离(d1,d2和d3)构造出粒子群结合模型退火算法的适应度函数为:

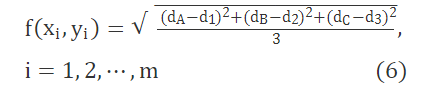
3.2 PSO-SA优化算法的步骤
利用PSO-SA混合群智能算法优化质心定位算法的基本思想是:首先,利用RSSI模型实现参考节点与未知节点距离的测定,进而确定未知节点的邻居节点;然后,利用邻居节点构造出围绕未知节点的三角形;最后,利用PSO-SA混合群智能算法对上节中构造的适应度函数进行寻优求解,实现对未知节点位置信息的确定,其中PSO-SA混合群智能算法的步骤如下。

步骤1 初始化粒子群和模拟退火算法。
1)粒子群算法的初始化:
群粒子的初始位置为3个参考节点的质心x(i)=(xi,yi)=(xA,yA)+(xB,yB)+(xC,yC)3;粒子速度初始化为vi=rand;设置每个粒子的最优位置pi=(xi,yi)和最优位置的起始值pbest=f(xi,yi);初始化群粒子中的最后一个粒子的解作为全局最优解,然后与其他粒子的最优解进行比较取最小解的位置作为全局最优解的位置pall=(xi,yi),并将全局搜索的极值设为groupFit。

2)模拟退火算法的初始化:
初始化退火常数K,初始温度T=f(pall)log5。
步骤2 当模拟退火系统的能量状态从E1变化到E2时利用Metropolis算法准则:

步骤3 更新位置x(i)和速度v(i),r1和r2都是随机数。
v(i+1)=wv(i)+c1r1(i)(pi-x(i))+c2r2(i)*(pall_plus-x(i)) (8)
x(i+1)=x(i)+v(i+1) (9)
步骤4 判断新的粒子群个体是否是最优位置和最优解,是否是粒子群全局最优解和最优位置。然后更新每次迭代后最优解的位置。更新权重系数w(n+1)=w(n)−0.5N。
步骤5 退火操作T(n+1)=KT(n),n=1,2,…,N。
步骤6 直至迭代结束,得到最优解的位置,否则转至步骤2完成迭代次数。
综上所述,PSO-SA混合群智能算法的流程图如图1所示。

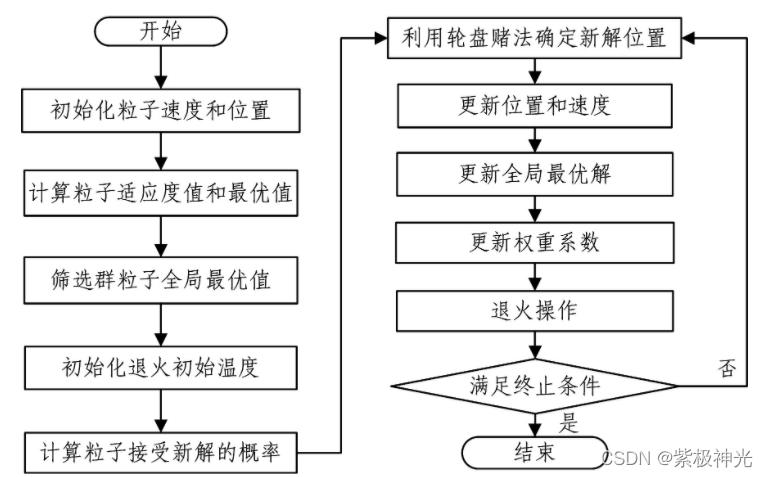
图1 PSO-SA混合群智能算法的流程

二、部分源代码

%信标节点位于等边三角形顶点的仿真 
clc 
clear all 
%S为三个选定的信标节点坐标矩阵,节点坐标已知(为便于仿真及验证,代码中采用的等边三角形)
%依次测试信标节点间距离放大t倍时的定位效果
for t = 1:10 
    S=[0,0;5*t,5*t*sqrt(3);10*t,0]; 
    nums = [S(1,1),S(1,2),S(2,1),S(2,2),S(3,1),S(3,2)]; 
    p = min(nums); 
    q = max(nums); 
    L = sqrt((S(1,1)-S(3,1))^2+(S(1,2)-S(3,2))^2); 
    m = 100; 
    %生成在[p,q]上满足均匀分布的随机数矩阵 
    %即生成一组m行2列的有可能落在等边三角形区域内的坐标 
    numbox = p+(q-p)*rand(m,2); 
     
    %计数初值,最终根据计算将随机生成的点中落在等边三角形区域内的坐标存放于新的矩阵 
    n = 1; 
    for i = 1:m 
        dA(i) = sqrt((numbox(i,1)-S(1,1))^2+(numbox(i,2)-S(1,2))^2); 
        dB(i) = sqrt((numbox(i,1)-S(2,1))^2+(numbox(i,2)-S(2,2))^2); 
        dC(i) = sqrt((numbox(i,1)-S(3,1))^2+(numbox(i,2)-S(3,2))^2); 
        %将确实在等边三角形区域内的坐标存入P_position矩阵 
        if (dA(i)<=L) && (dB(i)<=L) && (dC(i)<=L) 
            P_position(n,1) = numbox(i,1); 
            P_position(n,2) = numbox(i,2); 
            n = n+1; 
        end 
    end 
    %N为随机生成的点中落在等边三角形区域内的点(测试点)的个数 
    N = n-1 
    if N == 0 
        disp('所取的随机坐标无一落在等边三角形内,请增大m值重新运行程序.') 
        return 
    end 
 
    %计算测试点离三个顶点的实际距离 
    %dis为N行3列的矩阵,用于存放N个测试点分别到等边三角形三个顶点A,B,C的实际距离 
    for i = 1:N 
        dis(i,1) = sqrt((P_position(i,1)-S(1,1))^2+(P_position(i,2)-S(1,2))^2); 
        dis(i,2) = sqrt((P_position(i,1)-S(2,1))^2+(P_position(i,2)-S(2,2))^2); 
        dis(i,3) = sqrt((P_position(i,1)-S(3,1))^2+(P_position(i,2)-S(3,2))^2); 
    end 
 
    %根据函数Distance计算测试点离三个顶点的测试距离(考虑了衰减及环境误差等) 
    %dis_test为N行3列的矩阵,用于存放N个测试点分别到等边三角形三个顶点A,B,C的测试距离 
    a = 7; %由RSSI计算T-R距离时使用的参数 
    for i = 1:N 
        dis_test(i,1) = Distance(dis(i,1),a); 
        dis_test(i,2) = Distance(dis(i,2),a); 
        dis_test(i,3) = Distance(dis(i,3),a); 
    end 
     
    %根据函数Triangle及求得的测试距离进行定位 
    %P_calculate为N行2列的矩阵,用于存放定位后的N个坐标 
    for i = 1:N 
        [P_temp_SAPSO,fv]= SAPSO(@fitness,500,2,2,0.6,20,2,S,dis_test(i,1),dis_test(i,2),dis_test(i,3)); 
        P_calculate_SAPSO(i,1) = P_temp_SAPSO(1); 
        P_calculate_SAPSO(i,2) = P_temp_SAPSO(2); 
        P_temp = Triangle(S,dis_test(i,1),dis_test(i,2),dis_test(i,3));
        P_calculate_Triangle(i,1) = P_temp(1); 
        P_calculate_Triangle(i,2) = P_temp(2); 
    end 
    
    %由于测试距离相比真实距离有误差,三角计算中的两圆有可能无交点,导致方程无实根. 
    %于是P_calculate中会出现虚数.在测试中虚数无实际意义,因此取其实部存放于另一矩阵 
    for i = 1:N 
        P_calculate_Triangle_real(i,1) = real(P_calculate_Triangle(i,1)); 
        P_calculate_Triangle_real(i,2) = real(P_calculate_Triangle(i,2)); 
    end 
 
    %对比测试点的定位坐标与实际坐标之间的误差 
    P_position; 
    P_calculate_SAPSO;
    P_calculate_Triangle_real;
    %计算定位结果与真实坐标之间的距离误差平均值e_average(测试点等概率) 
    e_sum_SAPSO = 0; 
    e_sum_Triangle=0;
    e_max_SAPSO=0;
    e_max_Triangle=0;
    for i = 1:N 
        e_SAPSO = sqrt((P_calculate_SAPSO(i,1)-P_position(i,1))^2+(P_calculate_SAPSO(i,2)-P_position(i,2))^2); 
        if e_SAPSO>e_max_SAPSO
            e_max_SAPSO=e_SAPSO;
        end
        e_sum_SAPSO = e_sum_SAPSO+e_SAPSO; 
        e_Triangle=sqrt((P_calculate_Triangle_real(i,1)-P_position(i,1))^2+(P_calculate_Triangle_real(i,2)-P_position(i,2))^2);
        if e_Triangle>e_max_Triangle
            e_max_Triangle=e_Triangle;
        end
        e_sum_Triangle=e_sum_Triangle+e_Triangle;
    end 
    e_average_SAPSO = e_sum_SAPSO/N; 
    e_average_SAPSO_box(t)=e_average_SAPSO
    e_average_Triangle=e_sum_Triangle/N;
    e_average_Triangle_box(t)=e_average_Triangle
    e_max_SAPSO_box(t)=e_max_SAPSO
    e_max_Triangle_box(t)=e_max_Triangle
    e_average_percent_SAPSO = e_average_SAPSO/L; 
    e_average_percent_SAPSO_box(t)= e_average_percent_SAPSO
    e_average_percent_Triangle = e_average_Triangle/L;
    e_average_percent_Triangle_box(t)=e_average_percent_Triangle
end 
 
t = [1:10]; 
figure;
plot(t,e_average_SAPSO_box(t),'k-',t,e_average_Triangle_box(t),'k-.')
xlabel('t')
ylabel('平均定位误差')
legend('SAPSO','Triangle')
grid on;
figure;
plot(t,e_max_SAPSO_box(t),'k-',t,e_max_Triangle_box(t),'k-.')
xlabel('t')
ylabel('最大定位误差')
legend('SAPSO','Triangle')
grid on;
figure;
plot(t,e_average_percent_SAPSO_box(t),'k-',t, e_average_percent_Triangle_box(t),'k-.')
xlabel('t')
ylabel('平均定位误差率')
legend('SAPSO','Triangle')
grid on;



  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]王改云,王磊杨,路皓翔.基于混合群智能算法优化的RSSI质心定位算法[J].计算机科学. 2019,46(09)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/123397667