【BiLSTM数据预测】基于matlab双向长短时记忆BiLSTM数据预测【含Matlab源码 1793期】

一、双向长短时记忆（biLSTM）简介

1 LSTM网络基本原理
LSTM在RNN的基础上增加了单元状态，并引入内部“门”机制调节信息流，避免RNN出现的“梯度爆炸”和“梯度消失问题”。LSTM的结构算法为：
ft=σ(Wf·[ht-1,xt]+bf) (4)
it=σ(Wi·[ht-1,xt]+bi) (5)
c˜t=tanh(Wc)⋅[ht−1,xt]+bc)         (6)ct=ft⋅ct−1+it⋅c˜t         (7)ot=σ(W0⋅[ht−1,xt]+bo)         (8)ht=ot⋅tanh(ct)         (9)
式中，ft、it、c˜、ct、ot、ht分别为遗忘门、输入门、临时状态量、状态量、输出和最终输出单元值；W和b分别为各“门”对应的权重和偏置项；xt为输入向量；σ为将实数映射到[0,1]的sigmoid函数；tanh为将实数映射到[-1,1]的双曲正切函数。

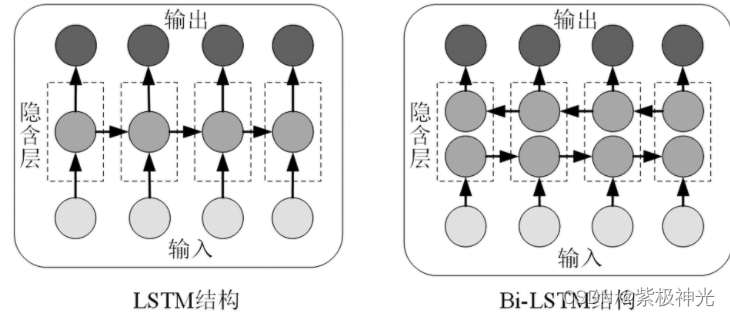
图1 LSTM与Bi-LSTM网络的对比示意图

2 双向LSTM基本原理
Bi-LSTM网络是标准LSTM网络的扩展，当网络学习完整的时序规律时，Bi-LSTM网络可以在不增加数据量的情况下，学习序列数据与时间步长之间的双向依赖关系。如图1所示，Bi-LSTM网络和LSTM网络的主要区别在于后者只保存过去的信息,而Bi-LSTM网络结合这两种隐含状态，可以同时保存过去和未来的信息。

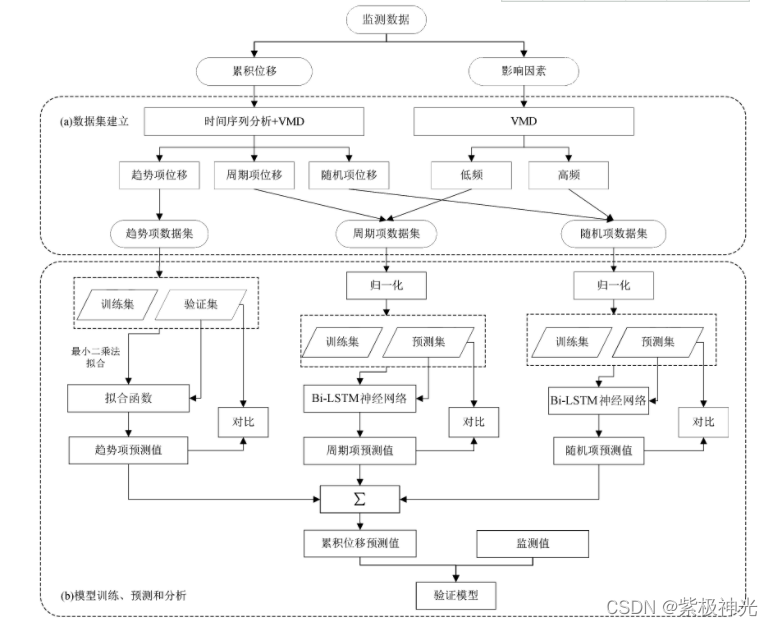
图2 位移预测流程图

二、部分源代码

clc
clear
close all
%%
load final.mat
for i=1:size(record,2)
    record(:,i)=record(:,i)/max(record(:,i));
end



  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
 

三、运行结果

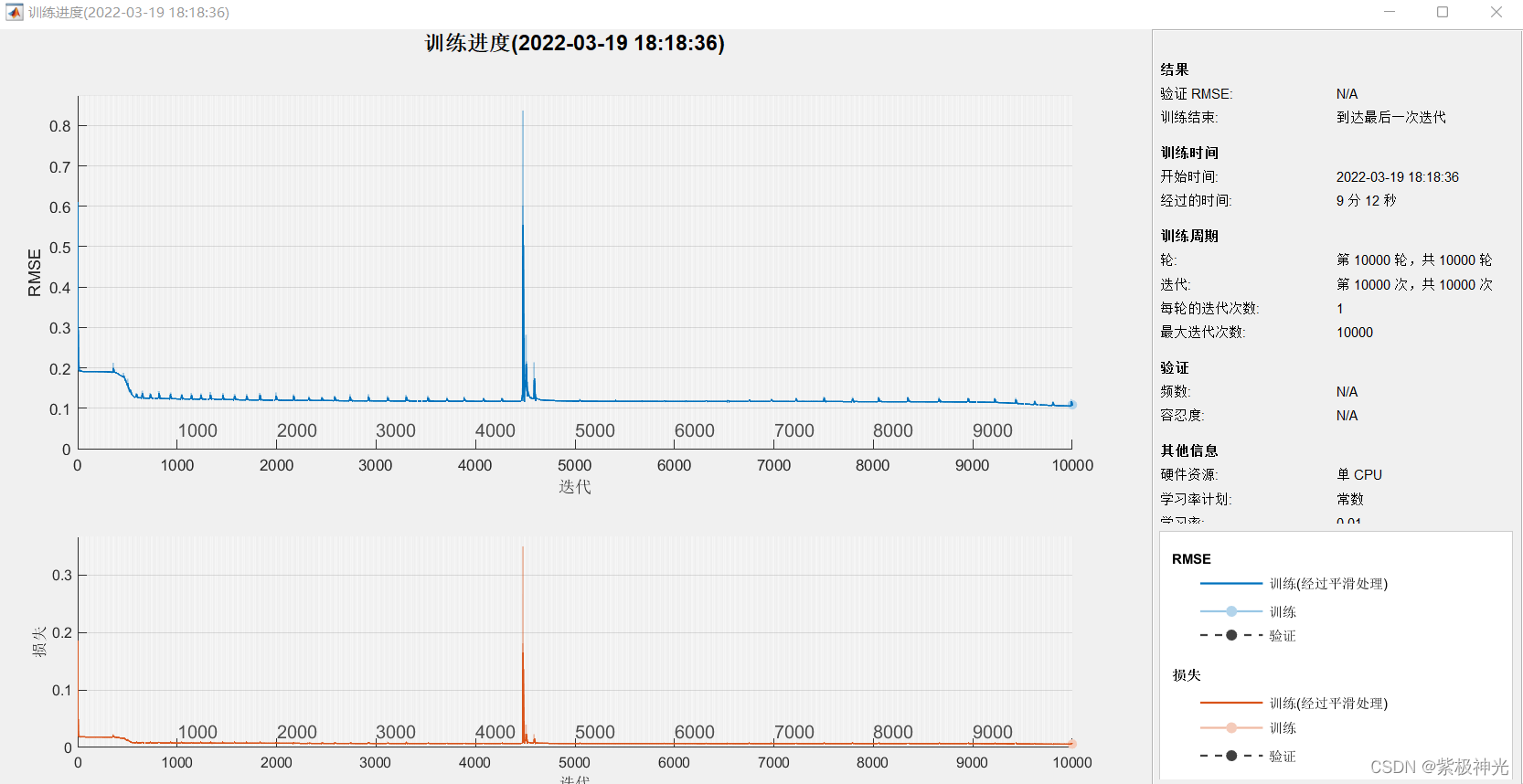
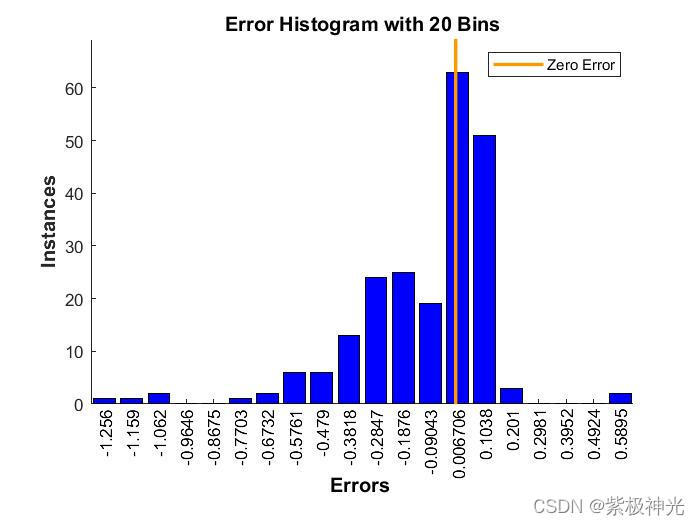
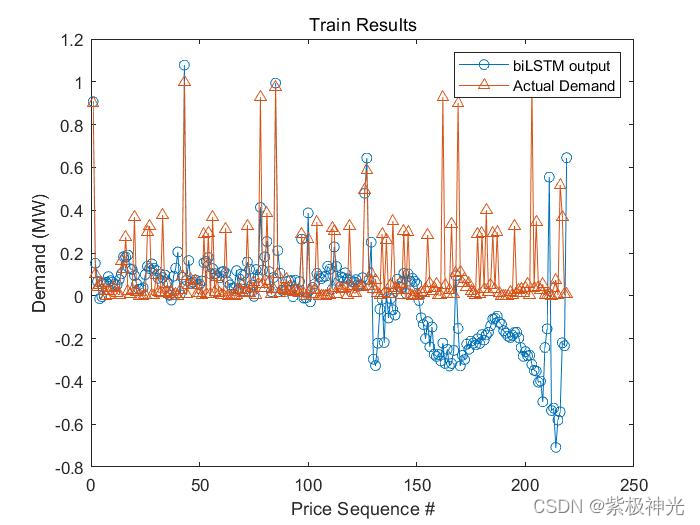
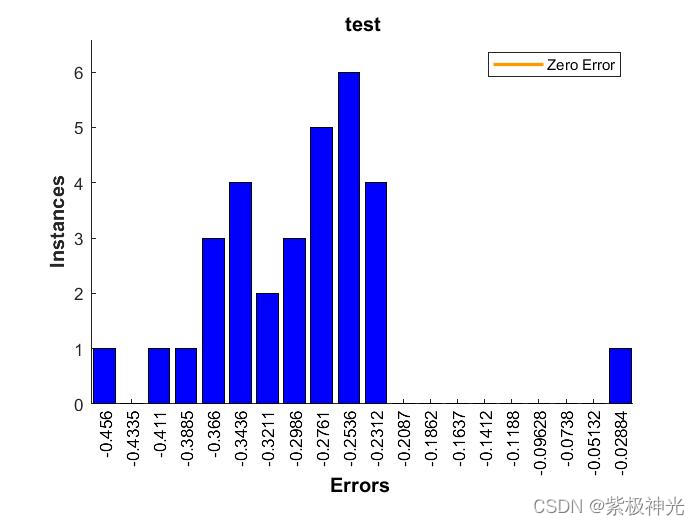
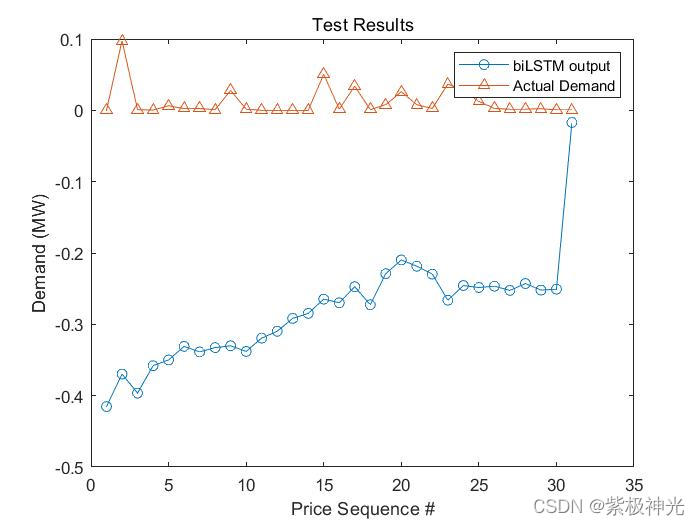
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.
[6]张明岳,李丽敏,温宗周.基于变分模态分解和双向长短时记忆神经网络模型的滑坡位移预测[J].山地学报. 2021,39(06)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/123633046