【LSTM时间序列预测】基于matlab贝叶斯优化LSTM时间序列预测（单变量单输出）【含Matlab源码 651期】

一、贝叶斯网络及LSTM简介

1 贝叶斯网络
贝叶斯网络(Bayesian network)，又称信念网络(Belief Network)，或有向无环图模型(directed acyclic graphical model)，是一种概率图模型，于1985年由Judea Pearl首先提出。它是一种模拟人类推理过程中因果关系的不确定性处理模型，其网络拓朴结构是一个有向无环图(DAG)。

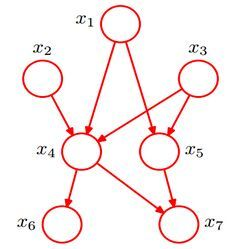
贝叶斯网络的有向无环图中的节点表示随机变量{ X 1 , X 2 , . . . , X n }
它们可以是可观察到的变量，或隐变量、未知参数等。认为有因果关系（或非条件独立）的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(children)”，两节点就会产生一个条件概率值。
例如，假设节点E直接影响到节点H，即E→H，则用从E指向H的箭头建立结点E到结点H的有向弧(E,H)，权值(即连接强度)用条件概率P(H|E)来表示，如下图所示：

简言之，把某个研究系统中涉及的随机变量，根据是否条件独立绘制在一个有向图中，就形成了贝叶斯网络。其主要用来描述随机变量之间的条件依赖，用圈表示随机变量(random variables)，用箭头表示条件依赖(conditional dependencies)。
此外，对于任意的随机变量，其联合概率可由各自的局部条件概率分布相乘而得出：

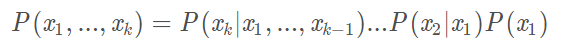
2.4.1 贝叶斯网络的结构形式
（1） head-to-head

依上图，所以有：P(a,b,c) = P(a)*P(b)P(c|a,b)成立，即在c未知的条件下，a、b被阻断(blocked)，是独立的，称之为head-to-head条件独立。
（2） tail-to-tail

考虑c未知，跟c已知这两种情况：
在c未知的时候，有：P(a,b,c)=P©P(a|c)P(b|c)，此时，没法得出P(a,b) = P(a)P(b)，即c未知时，a、b不独立。
在c已知的时候，有：P(a,b|c)=P(a,b,c)/P©，然后将P(a,b,c)=P©P(a|c)P(b|c)带入式子中，得到：P(a,b|c)=P(a,b,c)/P© = P©P(a|c)*P(b|c) / P© = P(a|c)*P(b|c)，即c已知时，a、b独立。
（3）head-to-tail

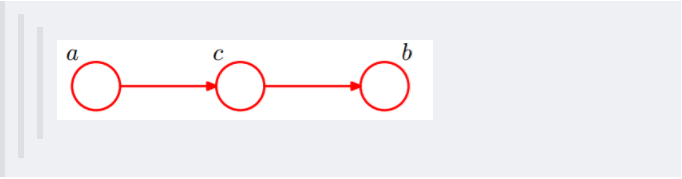
还是分c未知跟c已知这两种情况：
c未知时，有：P(a,b,c)=P(a)*P(c|a)*P(b|c)，但无法推出P(a,b) = P(a)P(b)，即c未知时，a、b不独立。
c已知时，有：P(a,b|c)=P(a,b,c)/P©，且根据P(a,c) = P(a)P(c|a) = P©P(a|c)，可化简得到：

所以，在c给定的条件下，a，b被阻断(blocked)，是独立的，称之为head-to-tail条件独立。
这个head-to-tail其实就是一个链式网络，如下图所示：

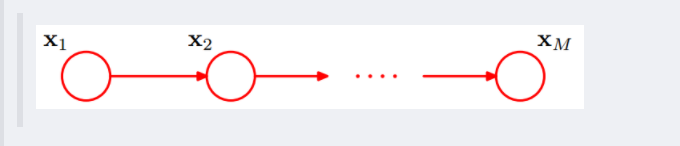
根据之前对head-to-tail的讲解，我们已经知道，在xi给定的条件下，xi+1的分布和x1,x2…xi-1条件独立。意味着啥呢？意味着：xi+1的分布状态只和xi有关，和其他变量条件独立。通俗点说，当前状态只跟上一状态有关，跟上上或上上之前的状态无关。这种顺次演变的随机过程，就叫做马尔科夫链（Markov chain）。对于马尔科夫链我们下一节再细讲。

2 LSTM简介
2.1 LSTM控制流程
LSTM的控制流程：是在前向传播的过程中处理流经细胞的数据，不同之处在于 LSTM 中细胞的结构和运算有所变化。

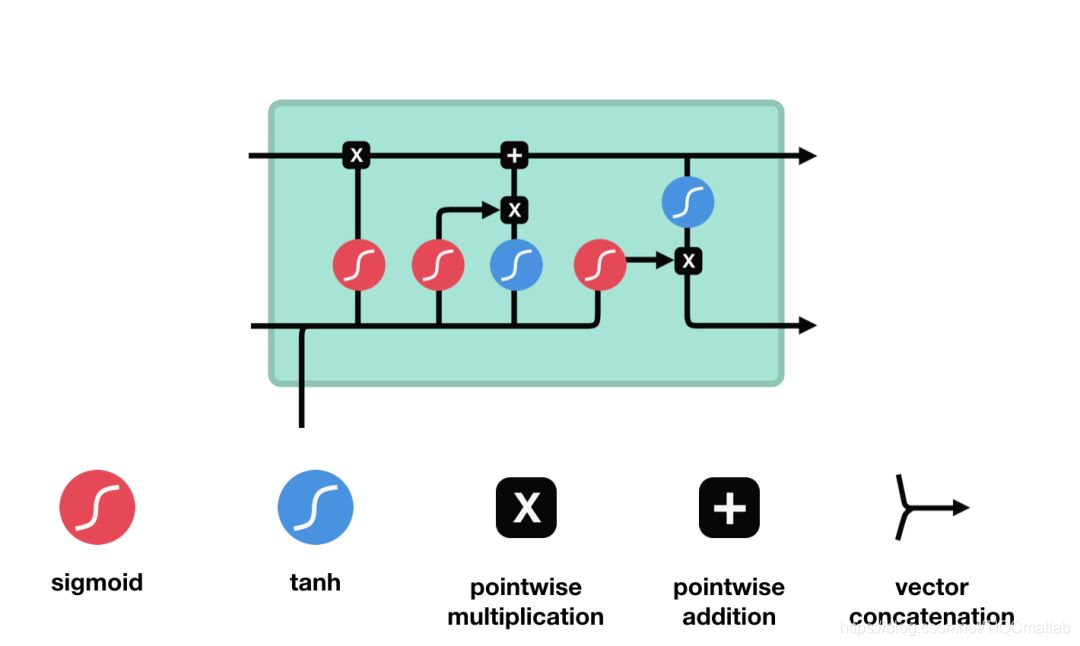
这一系列运算操作使得 LSTM具有能选择保存信息或遗忘信息的功能。咋一看这些运算操作时可能有点复杂，但没关系下面将带你一步步了解这些运算操作。

2.2 核心概念
LSTM 的核心概念在于细胞状态以及“门”结构。细胞状态相当于信息传输的路径，让信息能在序列连中传递下去。你可以将其看作网络的“记忆”。理论上讲，细胞状态能够将序列处理过程中的相关信息一直传递下去。
因此，即使是较早时间步长的信息也能携带到较后时间步长的细胞中来，这克服了短时记忆的影响。信息的添加和移除我们通过“门”结构来实现，“门”结构在训练过程中会去学习该保存或遗忘哪些信息。

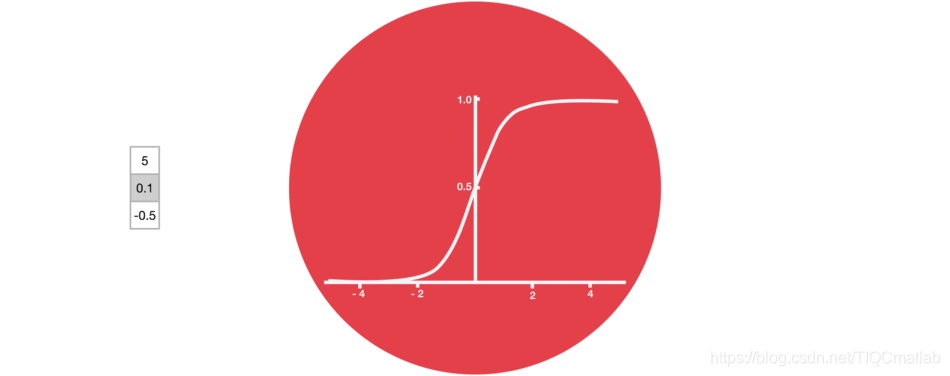
2.3 Sigmoid
门结构中包含着 sigmoid 激活函数。Sigmoid 激活函数与 tanh 函数类似，不同之处在于 sigmoid 是把值压缩到 0~1 之间而不是 -1~1 之间。这样的设置有助于更新或忘记信息，因为任何数乘以 0 都得 0，这部分信息就会剔除掉。同样的，任何数乘以 1 都得到它本身，这部分信息就会完美地保存下来。这样网络就能了解哪些数据是需要遗忘，哪些数据是需要保存。

2.4 LSTM门结构
LSTM 有三种类型的门结构：遗忘门、输入门和输出门。
2.4.1 遗忘门
遗忘门的功能是决定应丢弃或保留哪些信息。来自前一个隐藏状态的信息和当前输入的信息同时传递到 sigmoid 函数中去，输出值介于 0 和 1 之间，越接近 0 意味着越应该丢弃，越接近 1 意味着越应该保留。

2.4.2 输入门
输入门用于更新细胞状态。首先将前一层隐藏状态的信息和当前输入的信息传递到 sigmoid 函数中去。将值调整到 0~1 之间来决定要更新哪些信息。0 表示不重要，1 表示重要。
其次还要将前一层隐藏状态的信息和当前输入的信息传递到 tanh 函数中去，创造一个新的侯选值向量。最后将 sigmoid 的输出值与 tanh 的输出值相乘，sigmoid 的输出值将决定 tanh 的输出值中哪些信息是重要且需要保留下来的。

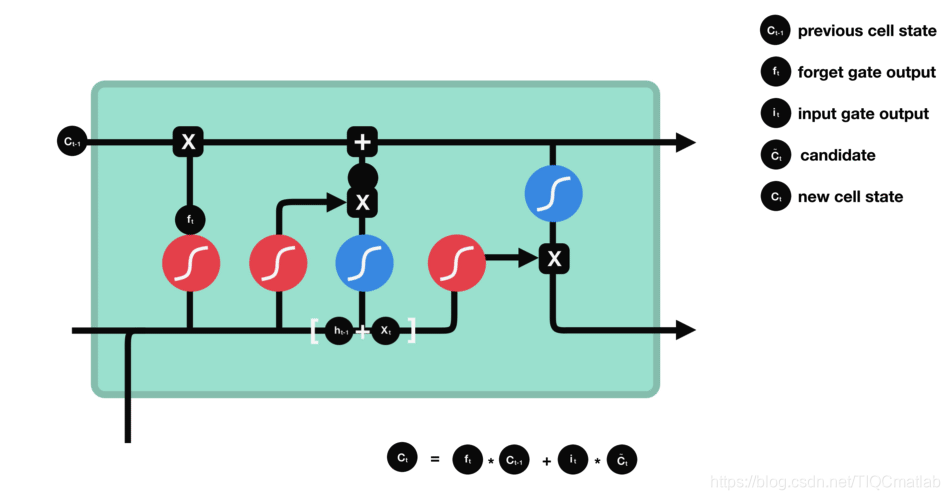
2.4.3 细胞状态
下一步，就是计算细胞状态。首先前一层的细胞状态与遗忘向量逐点相乘。如果它乘以接近 0 的值，意味着在新的细胞状态中，这些信息是需要丢弃掉的。然后再将该值与输入门的输出值逐点相加，将神经网络发现的新信息更新到细胞状态中去。至此，就得到了更新后的细胞状态。

2.4.4 输出门
输出门用来确定下一个隐藏状态的值，隐藏状态包含了先前输入的信息。首先，我们将前一个隐藏状态和当前输入传递到 sigmoid 函数中，然后将新得到的细胞状态传递给 tanh 函数。
最后将 tanh 的输出与 sigmoid 的输出相乘，以确定隐藏状态应携带的信息。再将隐藏状态作为当前细胞的输出，把新的细胞状态和新的隐藏状态传递到下一个时间步长中去。

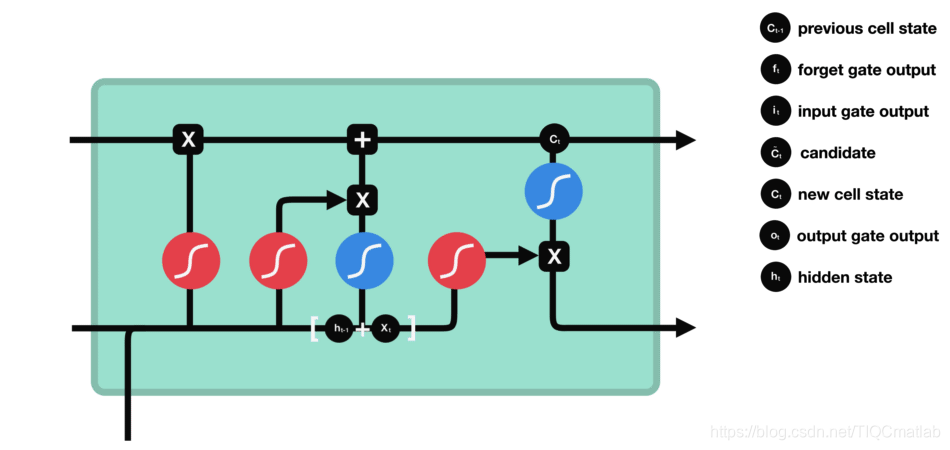
让我们再梳理一下。遗忘门确定前一个步长中哪些相关的信息需要被保留；输入门确定当前输入中哪些信息是重要的，需要被添加的；输出门确定下一个隐藏状态应该是什么。

二、部分源代码

  

 

  
1
 

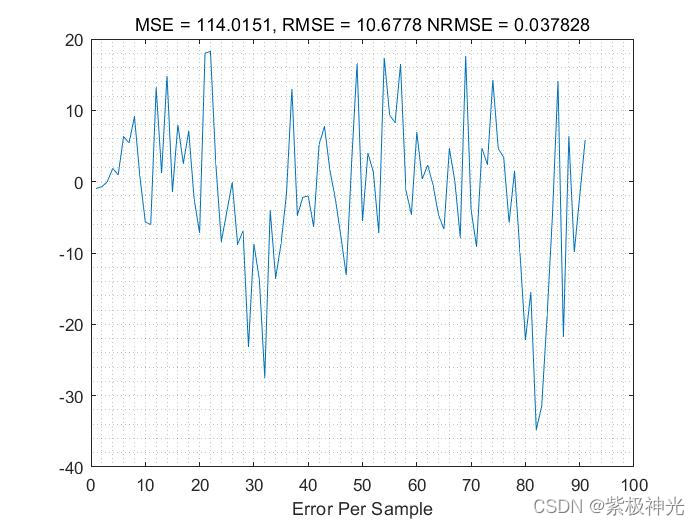
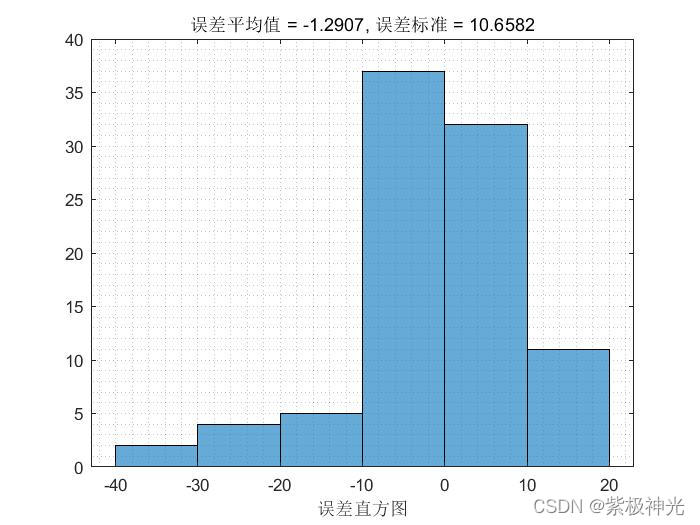
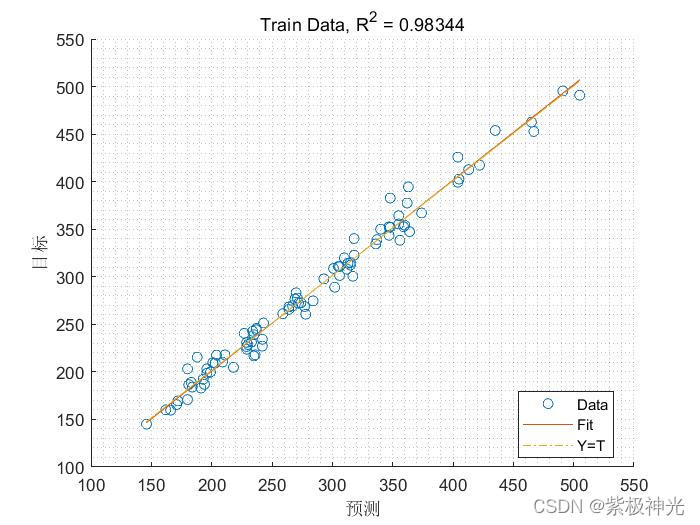
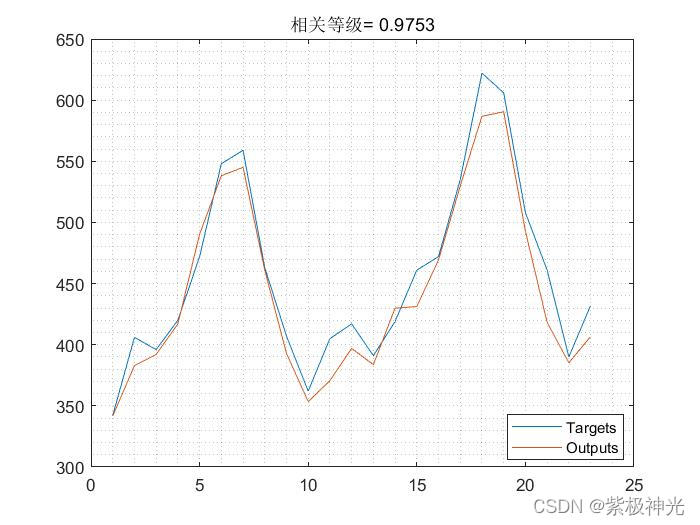
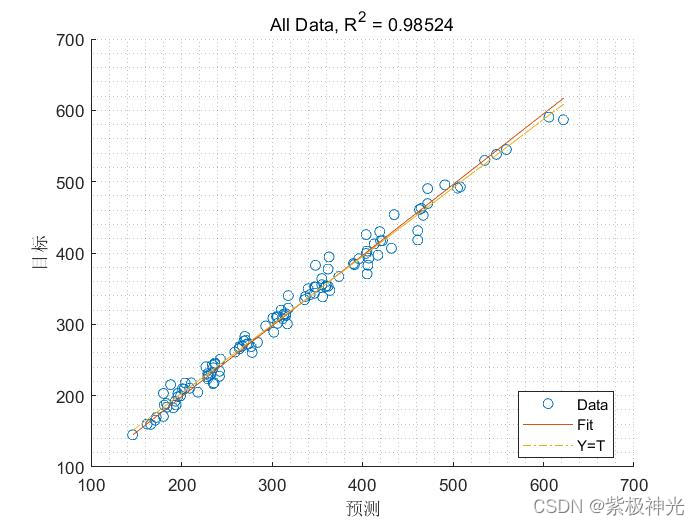
三、运行结果

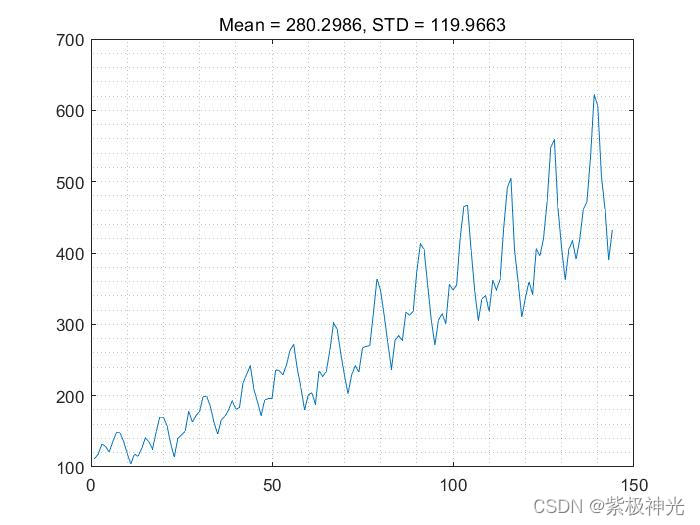
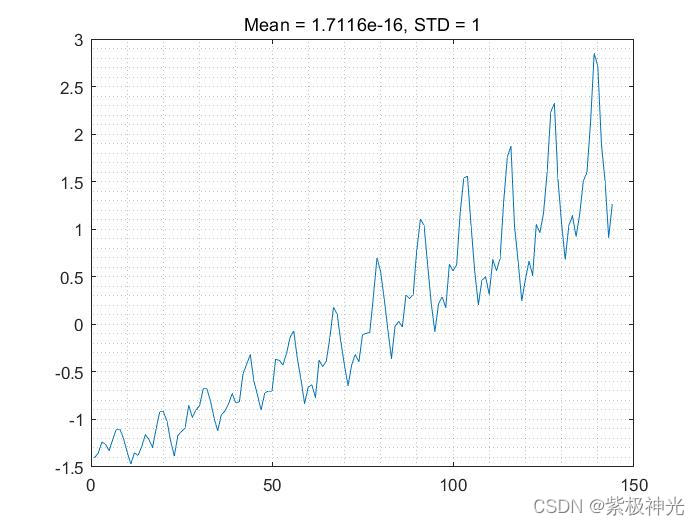
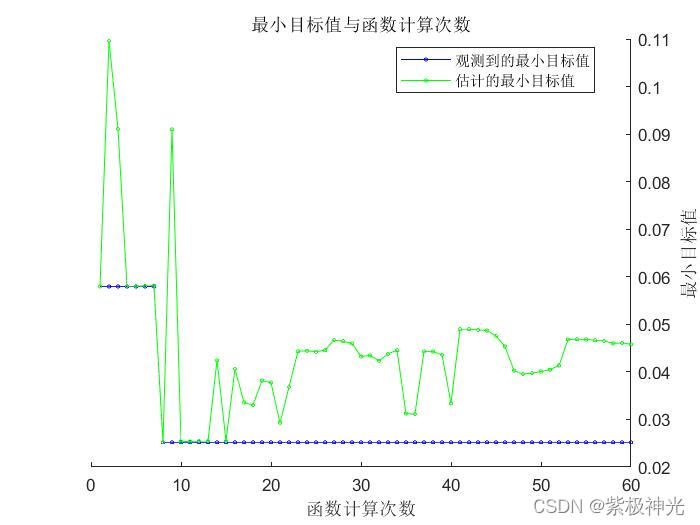
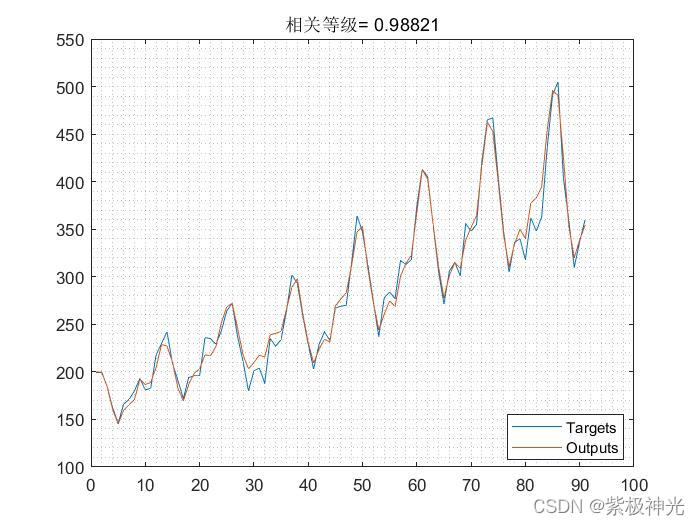
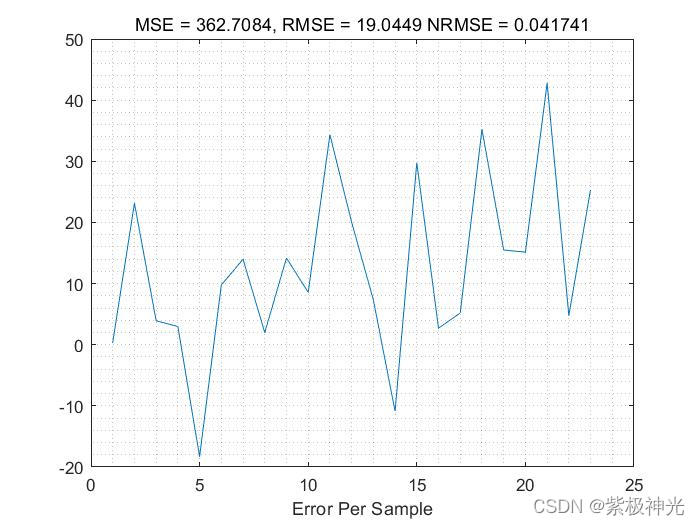
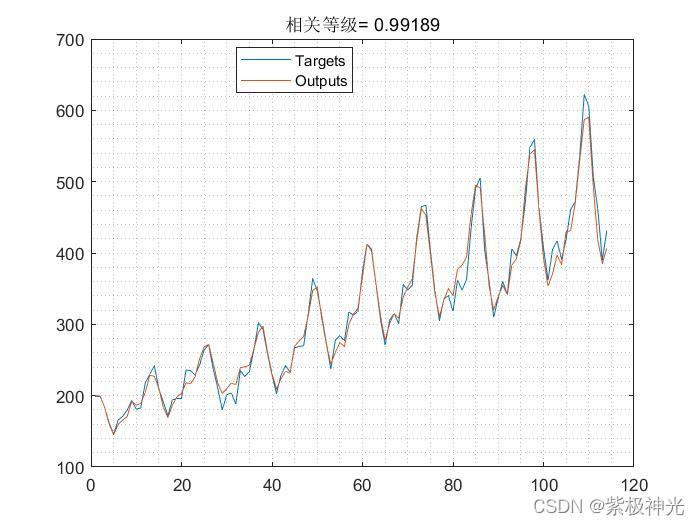
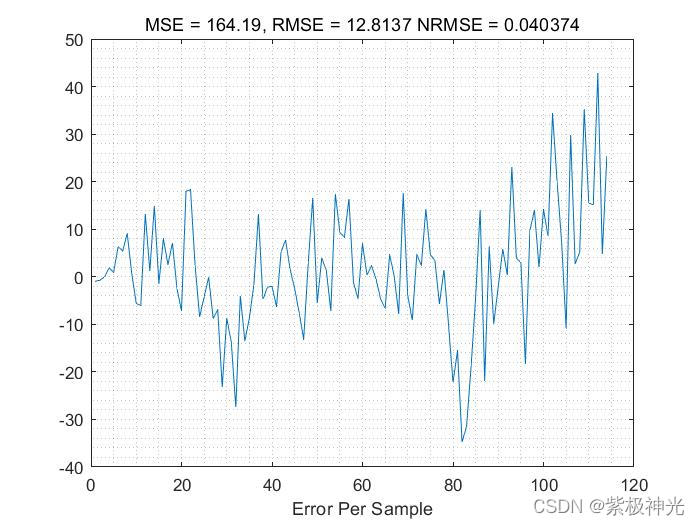
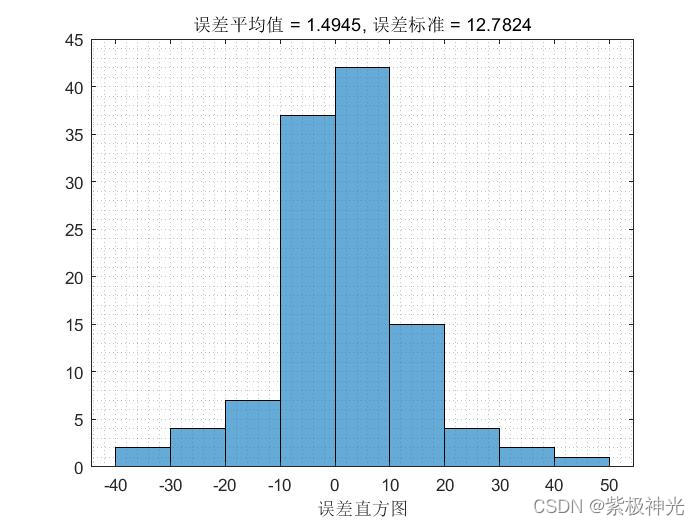
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/123956627