【SVM时间序列预测】基于matlab粒子群算法优化SVM时间序列预测【含Matlab源码 259期】

一、粒子群算法优化SVM预测简介

1 支持向量机方法
支持向量机的理论基础是结构风险最小化原则和VC维理论, 它是一种新型的机器学习方法, 并不是单纯地考虑经验风险, 还考虑了置信风险, 相比于传统的统计方法, 具有更强的推广能力, 能较好地解决非线性、高维度、局部极小等问题。SVM是在低维空间寻找最优分类面存在困难, 就将输入空间通过内积函数的变换映射到高维空间, 使得高维空间变得线性可分, 从而寻找到最优分类面。

在支持向量机方法中, 把线性可分推广到非线性可分, 引进适当的变换, 将原本在低维空间的训练点映射到高维Hilbert空间, 然后在高维空间中寻找一个超维平面, 使得这些样本点在高维空间中变得线性可分。在这个转化过程中, 最关键的就是找到这个非线性变换映射函数。Vapnik提出了核函数的方法, 该方法通过找到一个函数K (·, ·) , 使得K (xi, yj) =φ (xi) ·φ (xj) , 从而避免了高维的点积运算, 这样我们不需要知道映射函数φ (x) 的具体形式。

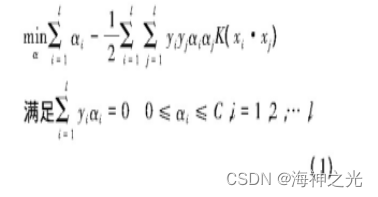
相应的决策函数为

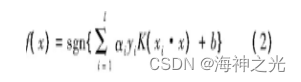
在实际问题中, 比较常见的是非线性问题, 而核函数的正确选取是解决非线性函数的关键。常见的核函数主要有3类, 分别是多项式核函数、高斯核函数和神经网络核函数。其中, 高斯核函数是效果最好的核函数, 这是因为它所对应的Hilbert空间的维数是无穷, 而有限训练样本在该Hilbert空间中肯定是线性可分的。由于该核函数只有一个参数σ, 寻优时间耗费比较少, 准确性也较高, 能很好解决许多问题。正是高斯核函数具有这种优势, 因而在工程实际中常被广泛应用。惩罚系数C和核函数参数σ是影响支持向量分类机的性能两个主要因素, 而核函数参数σ决定高斯核半径的大小, 若能选取合适的参数, 就能将训练样本在特征空间中正确分类。

在高斯核函数分类过程中, 针对事前预测的风险与实际存在风险承担的多少, 惩罚系数C能够很好地掌控与平衡, 将实际风险降到最低。对于某一个具体的分类问题, 在其样本空间中C取值过小时, 虽然置信风险很小, 但是经验风险值会很大, 此时的实际风险并未取得最小值, 称这种现象为“欠学习”。若参数C超过某一确定值后, 支持向量分类机的结构复杂性会变大, 经验风险和推广能力反而不会发生什么变化。

核函数是定义这样一个变换, 可以将平面上不能线性可分的训练点转换到高维空间, 从而能够在高维空间内线性可分。而高斯核函数的参数σ会影响这种变换关系, 影响训练点的可分性。经验风险的选择对降低实际风险具有很大的作用, 而经验风险又被参数σ所影响, 那么选择参数σ就得谨慎。由于置信风险随着VC维的增加而变小, 经验风险随着VC维的增加而变大, 所以要寻求一个合适的VC维使得经验风险和置信风险之和最小, 这样就需要找到一个合适的参数σ。

2 基于PSO—SVM的参数选择
按照上述分析, 为了能够得到较好的分类性能, 提高其泛化能力, 必须寻找合适的惩罚系数C和核函数参数σ。

在过去, 对于参数的选择方法有交叉验证法、网格搜索法、经验法, 但是这些方法寻找到一个合适的值耗费的时间比较长, 效率很低。所以, 可以考虑寻找一种更为迅速快捷的优化方式来对参数进行优化。PSO算法参数少, 容易实现, 在训练过程中, 对种群数量M、最大搜索次数N等参数的调整非常方便, 可以更快地获得优化的参数, 因此本文尝试使用PSO优化SVM分类器的参数。

2.1 交叉验证优化支持向量机参数选择
该方法的主要步骤如下:设定参数 (C, σ) , 且lg C∈[-10, 10], lgσ∈[-10, 10], 且对步长lg1网格搜索C和σ;选取全局最小值, 进而确定最优参数。其中,

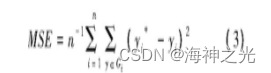
式中:n为样本总数;Gi为以第i个样本为验证样本的测试集;yi为第i个样本实际值;yi*为第i样本的SVM输出值。

十倍交叉验证就是将一个数据集划分成10份, 对其中1份进行轮流测试, 剩余9份作为训练集进行训练, 最后将10次结果的均值作为对算法精度的估计。这种精度测试方法虽然常用, 但判断时间相对较长, 判断率相对较低。

2.2 粒子群优化支持向量机的参数选择
粒子群算法不但能加速惩罚因子C和核函数参数σ的寻优过程, 也能达到较高的精度。为了更好提高粒子群算法的性能和效率, 选择最佳的参数是必不可少的。由于参数对支持向量机算法的性能影响很大, 因此, 对参数的选择变得非常重要。本文中利用粒子群算法的全局搜索能力和局部搜索能力, 可以对支持向量机建模过程中所需要的参数进行合理优化, 得到参数的最优解, 其算法流程图如下图1所示。

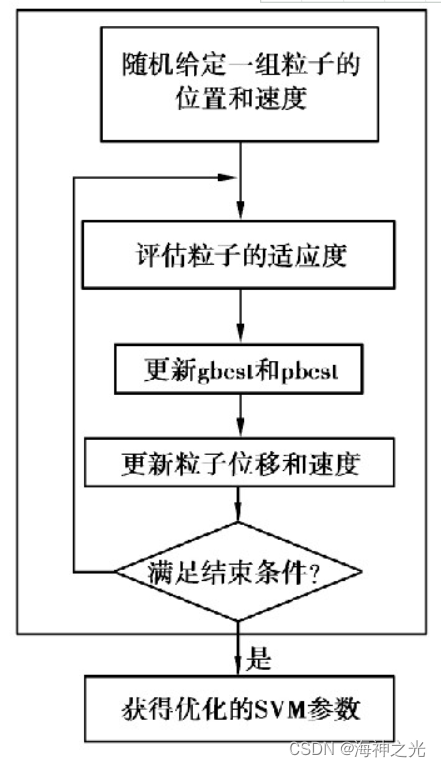
图1 粒子群优化支持向量机参数流程图

二、部分源代码

clear;clc;close all;
%% load Data;
data=xlsread('SVM训练数据-改.xls','负荷明细数据','B3:B6602');
% 6600/24=275天
%上一天24个数据作为输入 预测下一天的24个数据
for i=1:274
    X(i,:)=data((i-1)*24+1:i*24);
    Y(i,:)=data(i*24+1:(i+1)*24);
end
% 归一化
[inputn,inputps]=mapminmax(X',0,1);
X=inputn';
[outputn,outputps]=mapminmax(Y',0,1);
Y=outputn';



  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.
[6]汪华斌,卢自立,邱杰汉,刘文浩,张玲.基于粒子群算法优化支持向量机的岩爆预测研究[J].地下空间与工程学报. 2017,13(02)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/124528579