【FA TSP】基于matlab萤火虫算法求解旅行商问题【含Matlab源码 328期】

一、TSP简介

旅行商问题 (Travel Salesman Problem, TSP) 是最基本的路线问题, 其探索单一旅行者由起点出发, 并通过所有给定点后, 再回到起点的最小路径成本问题.求解TSP一直是组合优化领域研究的热点和难点问题之一.目前, 为解决TSP问题引入了各种智能算法, 如遗传算法、PSO算法、蚁群算法等, 然而这些方法存在计算存储量大、运行时间长、求解城市规模太小等不足.萤火虫算法 (Firefly Algorithm, FA) 是近年来提出的一种新型群智能算法, 已经在很多领域得到了应用, 通过模拟自然界中萤火虫的发光特性发展而来, 同蚁群算法、鱼群算法一样, 也是一种高级启发式算法.

1 标准萤火虫算法
1.1 标准萤火虫算法基本概念
萤火虫算法通过萤火虫个体之间的相互吸引达到寻优的目的, 具体来说, 就是由于萤火虫亮度的不同, 在一定范围内, 亮度小的萤火虫会被亮度大的萤火虫吸引, 从而逐渐向其移动.萤火虫的亮度与目标函数有关, 所以在萤火虫移动的过程结束后, 萤火虫会聚集在亮度最大的萤火虫位置, 即最优解, 这就是萤火虫算法的寻优过程.

1.2 标准萤火虫算法的数学描述与分析
萤火虫根据亮度不同进行选择移动.亮度分为绝对亮度和相对亮度.绝对亮度, 即萤火虫i在r=0处的光强度, 记为Ii, 绝对亮度由目标函数直接决定, 代表解的优劣程度;相对亮度, 即萤火虫i在萤火虫j处的光强度, 记为Iij, 表达为:

式中, γ为光吸收系数, 设为常数;rij为萤火虫i到萤火虫j的距离.

每个萤火虫都遵循吸引规则, 即绝对亮度小的萤火虫被绝对亮度大的萤火虫吸引, 吸引力与亮度成比例, 萤火虫i对萤火虫j的吸引力βij (rij) 为:

式中, β0为最大吸引力, 即在光源处 (r=0处) 萤火虫的吸引力.
假设萤火虫j被萤火虫i吸引, 向其移动, 移动后的新位置可根据位置更新公式计算, 表达为:

2 萤火虫算法TSP实现
2.1 编码
根据萤火虫算法的思想, 每个萤火虫可代表一组解, 假设城市的编号为:cities={1, 2, 3, …, n}, 那么每个萤火虫代表n个城市的任意排列, 即Path={p1, p2, p3, …, pi, …, pn}, pi代表途经的第i个城市.

2.2 绝对亮度

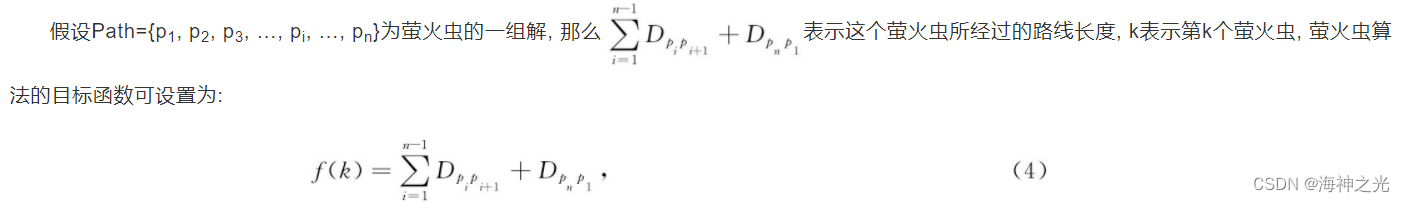
即目标函数的值越小, 路线长度越短.绝对亮度由目标函数直接决定, 代表解的优劣程度, 所以, 绝对亮度的公式可设置为:

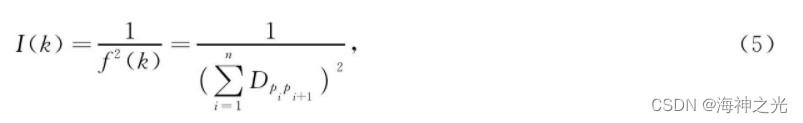
即路线长度越短, 萤火虫的绝对亮度值越大.

2.3 萤火虫个体间距公式
由式 (1) 可知, 相对亮度与绝对亮度Ii、光吸收系数γ和两萤火虫之间的距离rij有关.然而在TSP问题中, 每只萤火虫代表一组经过n个城市的随机序列, 所以, 在这重新定义萤火虫个体间的距离.假设萤火虫i的解为Path (i) ={pi1, pi2, pi3, …, pin}, 萤火虫j的解为Path (j) ={pj1, pj2, pj3, …, pjn}, rij则:

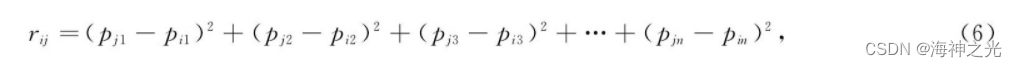
相对亮度公式和吸引力公式不变, 仍沿用式 (1) 、式 (2) .

2.4 位置更新公式
根据TSP问题解的特点, 每次位置更新并不能像式 (3) 一样, 即不能采用一只萤火虫向另一只萤火虫所在位置逐步移动这种方式, 而是在满足移动时直接移动到另一只萤火虫的位置, 即把另一只萤火虫的解直接赋值给当前的萤火虫.表示为:

二、部分源代码

clc;


  

 

  
1
  
2
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]胡楠,徐晓光.基于改进萤火虫算法的TSP问题[J].安徽工程大学学报. 2016,31(02)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/124577418