【基础教程】BP神经网络

1 BP神经网络的结构组成
BP神经网络结构组成：2输入1输出，5个隐含层的，也称为2-5-1网络结构；
Neural Network：神经网络
Input：输入
Hidden LayerOutput Layer：隐藏层输出层
Output Layer：输出层
Output ：输出

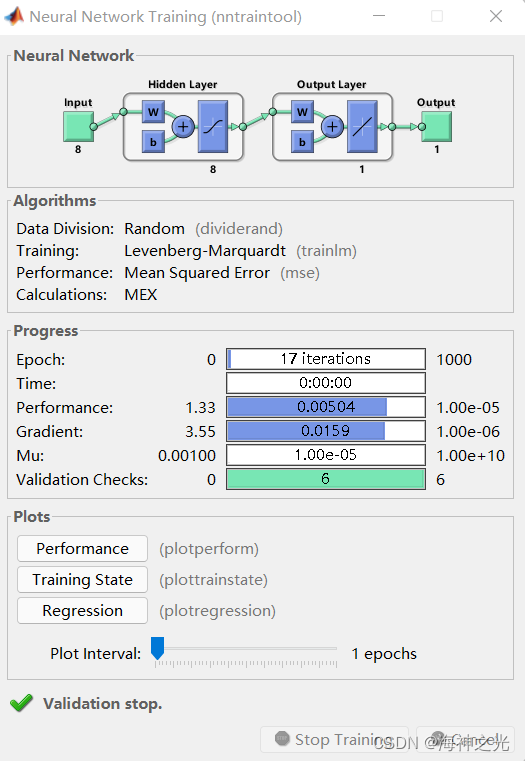
2 BP神经网络训练界面的参数
2.1 BP神经网络算法
Algorithms：算法
Data Division：Random(divider and) 数据划分：随机（除数和）
Training：Levenberg-Marquardt(train lm) 训练：表示训练采用的方法
Performance：Mean Squared Error(mse) 性能：均方误差(mse) 用均方误差衡量网络性能
Calculations：MEX 计算方式：MEX

2.2 BP神经网络进程
Progress 进程
Epoch： 训练次数
Time： 训练时间
Performance： 网络性能
Gradient： 梯度算子
Mu： 误差精度
Validation Checks： 泛化性（ 表示BP神经网络在训练过程中，如果均方误差（MSE）连续6次不降反升，则网络停止训练）

2.3 BP神经网络情节
Plots 绘图
Performance 网络性能
Training State 训练阶段参数变化情况
Regression 相关性分析

3 BP神经网络预测步骤
（1）读取数据
（2）设置训练数据和预测数据
（3）训练样本数据归一化
（4）构建BP神经网络
（5）网络参数配置(训练次数，学习速率，训练目标最小误差.等)
（5）BP神经网络训练
（6）测试样本归一化
（7）BP神经网络预测
（8）预测结果反归一化与误差计算
（8）验证集的真实值与预测值误差比较

4 BP神经网络预测案例代码

%% 此程序为matlab编程实现的BP神经网络
% 清空环境变量
clear
close all
clc

%%第一步 读取数据
input=randi([1 20],200,2);  %载入输入数据
output=input(:,1)+input(:,2);  %载入输出数据

%% 第二步 设置训练数据和预测数据
input_train = input(1:190,:)';
output_train =output(1:190,:)';
input_test = input(191:200,:)';
output_test =output(191:200,:)';
%节点个数
inputnum=2; % 输入层节点数量
hiddennum=5;% 隐含层节点数量
outputnum=1; % 输出层节点数量
%% 第三本 训练样本数据归一化
[inputn,inputps]=mapminmax(input_train);%归一化到[-1,1]之间，inputps用来作下一次同样的归一化
[outputn,outputps]=mapminmax(output_train);
%% 第四步 构建BP神经网络
net=newff(inputn,outputn,hiddennum,{'tansig','purelin'},'trainlm');% 建立模型，传递函数使用purelin，采用梯度下降法训练

W1= net. iw{1, 1};%输入层到中间层的权值
B1 = net.b{1};%中间各层神经元阈值

W2 = net.lw{2,1};%中间层到输出层的权值
B2 = net. b{2};%输出层各神经元阈值

%% 第五步 网络参数配置（ 训练次数，学习速率，训练目标最小误差等）
net.trainParam.epochs=1000;         % 训练次数，这里设置为1000次
net.trainParam.lr=0.01;                   % 学习速率，这里设置为0.01
net.trainParam.goal=0.00001;                    % 训练目标最小误差，这里设置为0.00001

%% 第六步 BP神经网络训练
net=train(net,inputn,outputn);%开始训练，其中inputn,outputn分别为输入输出样本

%% 第七步 测试样本归一化
inputn_test=mapminmax('apply',input_test,inputps);% 对样本数据进行归一化

%% 第八步 BP神经网络预测
an=sim(net,inputn_test); %用训练好的模型进行仿真

%% 第九步 预测结果反归一化与误差计算     
test_simu=mapminmax('reverse',an,outputps); %把仿真得到的数据还原为原始的数量级
error=test_simu-output_test;      %预测值和真实值的误差

%%第十步 真实值与预测值误差比较
figure('units','normalized','position',[0.119 0.2 0.38 0.5])
plot(output_test,'bo-')
hold on
plot(test_simu,'r*-')
hold on
plot(error,'square','MarkerFaceColor','b')
legend('期望值','预测值','误差')
xlabel('数据组数')
ylabel('样本值')
title('BP神经网络测试集的预测值与实际值对比图')

[c,l]=size(output_test);
MAE1=sum(abs(error))/l;
MSE1=error*error'/l;
RMSE1=MSE1^(1/2);
disp(['-----------------------误差计算--------------------------'])
disp(['隐含层节点数为',num2str(hiddennum),'时的误差结果如下：'])
disp(['平均绝对误差MAE为：',num2str(MAE1)])
disp(['均方误差MSE为：       ',num2str(MSE1)])
disp(['均方根误差RMSE为：  ',num2str(RMSE1)])


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
 

5 参考文献
[1] 周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[2]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[3]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/124655310