【前言】

今天是刷题打卡第53天！

加油啦各位。

原题：爬楼梯（记忆化搜索、简单DP） 

原题链接：力扣

题目描述：

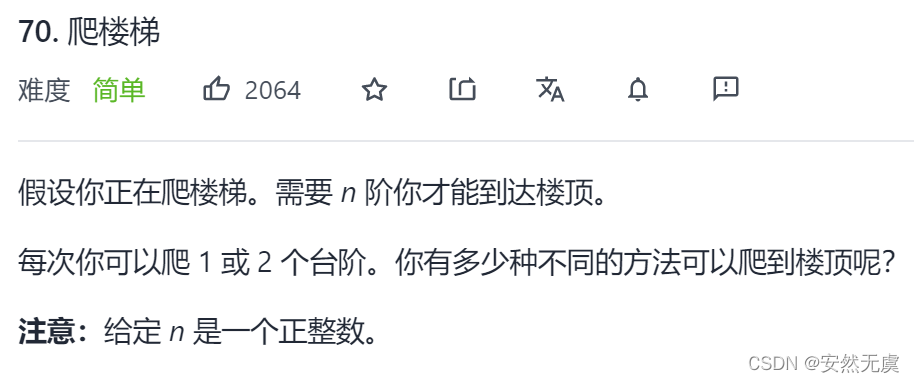
示例1：

  

   

    

     

    
    

     

      输入： 2
     
    
   

    

     

    
    

     

      输出： 2
     
    
   

    

     

    
    

     

      解释： 有两种方法可以爬到楼顶。
     
    
   

    

     

    
    

     

      1.  1 阶 + 1 阶
     
    
   

    

     

    
    

     

      2.  2 阶
     
    
  
 

示例2：

  

   

    

     

    
    

     

      输入： 3
     
    
   

    

     

    
    

     

      输出： 3
     
    
   

    

     

    
    

     

      解释： 有三种方法可以爬到楼顶。
     
    
   

    

     

    
    

     

      1.  1 阶 + 1 阶 + 1 阶
     
    
   

    

     

    
    

     

      2.  1 阶 + 2 阶
     
    
   

    

     

    
    

     

      3.  2 阶 + 1 阶
     
    
  
 

首先分析一下本题：

注意：注意这个题目问的是什么？

问的不是能爬多少次，而是有多少种方法能到最后一个台阶。

问题分析：当n > 2时，第一次爬就有两种不同的选择：一是第一次只爬一级，此时爬法数目等于后面剩下的（n - 1）级台阶的爬法数目，即为f(n - 1); 还有一种选择是第一次爬两级，此时爬法数目等于后面剩下的（n - 2）级台阶的爬法数目，即为f(n - 2).

所以有：f(n) = f(n - 1) + f(n - 2)

当n == 1时，有1种爬法；

当n == 2时，有2种爬法；

当n == 3时，有3种爬法；

当n == 4时，有5种爬法。

是呀，这题跟斐波那契数列基本上一样，不过这道题目需要思考一下，没有斐波那契这么明显。但是需要注意的是，递归边界还是有所不同的哦！

方法一：暴力递归

代码执行：

  

   

    

     

    
    

     

      class Solution {
     
    
   

    

     

    
    

     

      public:
     
    
   

    

     

    
    

     
    int climbStairs(int n) {
     
    
   

    

     

    
    

     
        //方法一：暴力递归
     
    
   

    

     

    
    

     
        //找边界
     
    
   

    

     

    
    

     
        if(n == 1){
     
    
   

    

     

    
    

     
            return 1;
     
    
   

    

     

    
    

     

              }
     
    
   

    

     

    
    

     
        if(n == 2){
     
    
   

    

     

    
    

     
            return 2;
     
    
   

    

     

    
    

     

              }
     
    
   

    

     

    
    

     
        return climbStairs(n - 1) + climbStairs(n - 2);
     
    
   

    

     

    
    

     

          }
     
    
   

    

     

    
    

     

      };
     
    
  
 

方法二：记忆化搜索（简单DP）

代码执行：

  

   

    

     

    
    

     

      class Solution {
     
    
   

    

     

    
    

     

      public:
     
    
   

    

     

    
    

     
    int climbStairs(int n) {
     
    
   

    

     

    
    

     
        //方法二:记忆化搜索（简单DP）
     
    
   

    

     

    
    

     
        //找边界
     
    
   

    

     

    
    

     
        if(n == 1){
     
    
   

    

     

    
    

     
            return 1;
     
    
   

    

     

    
    

     

              }
     
    
   

    

     

    
    

     
        if(n == 2){
     
    
   

    

     

    
    

     
            return 2;
     
    
   

    

     

    
    

     

              }
     
    
   

    

     

    
    

     
        //定义一个大小为n+1的整型数组，并且初始化为0
     
    
   

    

     

    
    

     
        vector<int> dp(n+1, 0);
     
    
   

    

     

    
    

     

              dp[1] = 1;
     
    
   

    

     

    
    

     

              dp[2] = 2;
     
    
   

    

     

    
    

     
        for(int i = 3; i < n+1; i++)
     
    
   

    

     

    
    

     

              {
     
    
   

    

     

    
    

     

                  dp[i] = dp[i - 1] + dp[i - 2];
     
    
   

    

     

    
    

     

              }
     
    
   

    

     

    
    

     
        return dp[n];
     
    
   

    

     

    
    

     

          }
     
    
   

    

     

    
    

     

      };
     
    
  
 

结语

今天是刷题打卡第53天！

加油吧少年。

文章来源: bit-runout.blog.csdn.net，作者：安然无虞，版权归原作者所有，如需转载，请联系作者。

原文链接：bit-runout.blog.csdn.net/article/details/121890091