《刷面试真题学数据结构·助你月薪提高3K》· 数据结构和算法那些事儿

大家好,我是安然无虞。
文章目录
每篇前言
博客主页:安然无虞
作者认证:2021年博客新星Top2
咱的口号:🌹小比特,大梦想🌹
作者请求:由于博主水平有限,难免会有错误和不准之处,我也非常渴望知道这些错误,恳请铁汁批评斧正。
火爆专栏:蓝桥杯基础算法剖析
欢迎加入:比特社区
【声明】
新的专栏:杭哥带我深度剖析数据结构
从今天开始会大量更新数据结构专栏的文章,带大家一起深度学习数据结构,同时呢也是为暑期准备开设的【系统且详细讲解算法】做准备,期待大家追更哦,当然,内容全部免费,欢迎订阅哈。
一、为什么&怎么做
1.为什么一定要学好数据结构?
首先,数据结构和算法是校招面试中必考察的部分,属于重中之重部分,简单看一下字节的招聘要求:
招聘要求:
再来看看一个简单的面经:
不单单是在面试找工作中,就是在学校开设的课程中以及考研,数据结构也都是常考的一门学科,所以很明显,数据结构和算法是非常重要的。
2.我们该如何学习呢?
学习数据结构和算法一定要多多画图实践
比如就拿我之前的一道数据结构题目来说吧:供学习的示例
原题链接:反转链表
题目描述:
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例:
解题思路1:翻指针方向
不过直接翻指针方向这个方法定义两个指针是翻不动的,需要定义三个指针,可能看下图很难理解,但是要结合代码去理解,最好自己能画一遍,尝试自己写一遍代码。初始代码:
struct ListNode* reverseList(struct ListNode* head) { //判断特殊情况 if(head == NULL) return NULL; struct ListNode* n1 = NULL, *n2 = head, *n3 = n2->next; while(n2) { n2->next = n1; n1 = n2; n2 = n3; //注意哦,当n3指向空指针时再执行n3 = n3->next;会导致空指针异常 if(n3) n3 = n3->next; } return n1; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
完整代码:
优化后的代码:
struct ListNode* reverseList(struct ListNode* head) { struct ListNode* n1 = NULL, *n2 = head; while(n2) { struct ListNode* n3 = n2->next; n2->next = n1; n1 = n2; n2 = n3; } return n1; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
是不是变得很简单,这样写也无需判断特殊情况。
完整代码:
解题思路2:头插法
之所以需要多定义一个指针,是因为要保证能找到下一个。
代码执行:struct ListNode* reverseList(struct ListNode* head) { struct ListNode* newHead = NULL; struct ListNode* cur = head; while(cur) { //之所以将next定义在循环里是为了防止head为空时造成野指针 struct ListNode* next = cur->next; cur->next = newHead; newHead = cur; cur = next; } return newHead; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
完整代码:
主要想讲的是,给我们一道题目,一上来不是直接开始写代码,而是先动手画图,先去分析常规情况,把常规情况的伪代码写下来,后面再去分析特殊边界情况,再补充伪代码部分,最后才是开始动手写代码,如果一开始不是按照这个步骤,很容易写出bug。
还有就是想学好数据结构一定要多做多见,多多实现数据结构,任重道远,一起加油吧兄弟们。

二、复杂度的概念
1.算法效率
算法效率有两种:一是时间效率;二是空间效率
2.时间复杂度
算法中基本操作的执行次数,为算法的时间复杂度
3.空间复杂度
对一个算法在运行的过程中临时占用存储空间大小的量度,不是指程度占用了多少字节的空间,因为这个没有太大意义,所以空间复杂度算的是变量的个数
4.大O渐进表示法
实际上,在计算复杂度时,属于量及评估,只需要知道大概的执情况,那么这里我们使用大O的渐进表示法表示它即可。
大O符号:用于描述函数渐进行为的数学符号。
注意:推到大O阶方法:
- 用常量1代替运行时间中的所有常数;
- 在修改后的运行次数函数中,只保留最高阶项;
- 如果最高阶项存在且不是1,则去除这个项的系数。
另外,有些算法的时间复杂度存在最好、平均和最坏的情况:
- 最坏情况:任意输入规模的最大运行次数(上界);
- 平均情况:任意输入规模的期望运行次数;
- 最好情况:任意输入规模的最小运行次数(下界)。
注意:在实际中时间复杂度一般关注的是最坏运行情况,所以数组中搜索数据的时间复杂度是O(N),这也就是说,当算法存在三种情况的时候,看最坏。
5.注意事项
- 时间复杂度不算时间,算执行次数;空间复杂度不算空间,算变量的个数。
- 时间是累积的,空间是不累计的,比如循环走了N次,重复利用的是同一块空间(往回走,会销毁,这个到后面的题目中会详细说明)

三、八大经典实例
在上手题目之前,大家先把这个性质再看一遍:
注意:推到大O阶方法:
- 用常量1代替运行时间中的所有常数;
- 在修改后的运行次数函数中,只保留最高阶项;
- 如果最高阶项存在且不是1,则去除这个项的系数。
实例一
Func1执行的基本操作数:F(N) = N^2 + 2*N +10;
很显然,随着N的增大,N^2对结果的影响最大,而时间复杂度是一个估算,是去看表达式中影响结果最大的那一项;
在这里呢,随着N无限大的时候,后两项对结果的影响可以忽略不计。
所以,本题:
时间复杂度:O(N^2)
空间复杂度:O(1)
实例二
本题:
时间复杂度:O(N+M)
空间复杂度:O(1)
若题干说明M远大于N,则时间复杂度:O(M);
如题干说明M远小于N,则时间复杂度:O(N).
实例三:类二分查找时间复杂度
注意,本题容易判断出错
时间复杂度:O(logN)
空间复杂度:O(1)
可能我们很容易会错写成O(N),这里我先暂时不说是为什么,请朝后看。
实例四
注意哦,本题时间复杂度不是O(100)
时间复杂度:O(1)
空间复杂度:O(1)
实例五
时间复杂度:O(N)
空间复杂度:O(1)
实例六:冒泡排序
思路分析:
实例七:二分查找
二分查找的时间复杂度跟实例三是一样的,每次砍掉一半:
实例八:递归调用
单路递归:例1
思路分析:
单路递归:例2
思路分析:
小总结:
- 每次递归调用是O(1),那么就看它的递归次数;
- 每次递归调用不是O(1),那么就看它的递归调用中次数的累加。
多路递归:斐波那契数列
解题思路:
对于递归的时间复杂度和空间复杂度需要注意的是:
- 时间一去不复返,是累积的;
- 空间回收以后可以重复利用。

四、细剖面试真题
【声明】
这两道题之前在每日一题中出现过,之所以放在这里是为了方便博主以后复习数据结构这块,所以大家如果看过了可以不用再看下面两题了。
面试一
题目链接:消失的数字
题目描述:
思路一:排序
思路二:映射方式(hash)
思路三:求和求差
代码执行:
思路四:异或法
如果大家对于位运算不是特别熟悉,可以看看我之前的一篇文章:位运算的奇巧淫计及其实战
代码执行:
面试二
思路一:保存挪放置三部曲
思路二:空间换时间
思路三:牛人找出的规律
代码执行://逆置函数 void reverse(int* nums, int left, int right) { while(left < right) { int temp = nums[left]; nums[left] = nums[right]; nums[right] = temp; left++; right--; } } void rotate(int* nums, int numsSize, int k) { k %= numsSize;//保证K的合法性 //第一步:后K个逆置 reverse(nums, numsSize - k, numsSize - 1); //第二步:前N-K个逆置 reverse(nums, 0, numsSize - k - 1); //第三步:整体逆置 reverse(nums, 0, numsSize - 1); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23

五、遇见安然遇见你,不负代码不负卿。
码字不易,求个三连。 抱拳了兄弟们。

文章来源: bit-runout.blog.csdn.net,作者:安然无虞,版权归原作者所有,如需转载,请联系作者。
原文链接:bit-runout.blog.csdn.net/article/details/123363907
- 点赞
- 收藏
- 关注作者


 招聘要求:
招聘要求: 再来看看一个简单的面经:
再来看看一个简单的面经: 不单单是在面试找工作中,就是在学校开设的课程中以及考研,数据结构也都是常考的一门学科,所以很明显,数据结构和算法是非常重要的。
不单单是在面试找工作中,就是在学校开设的课程中以及考研,数据结构也都是常考的一门学科,所以很明显,数据结构和算法是非常重要的。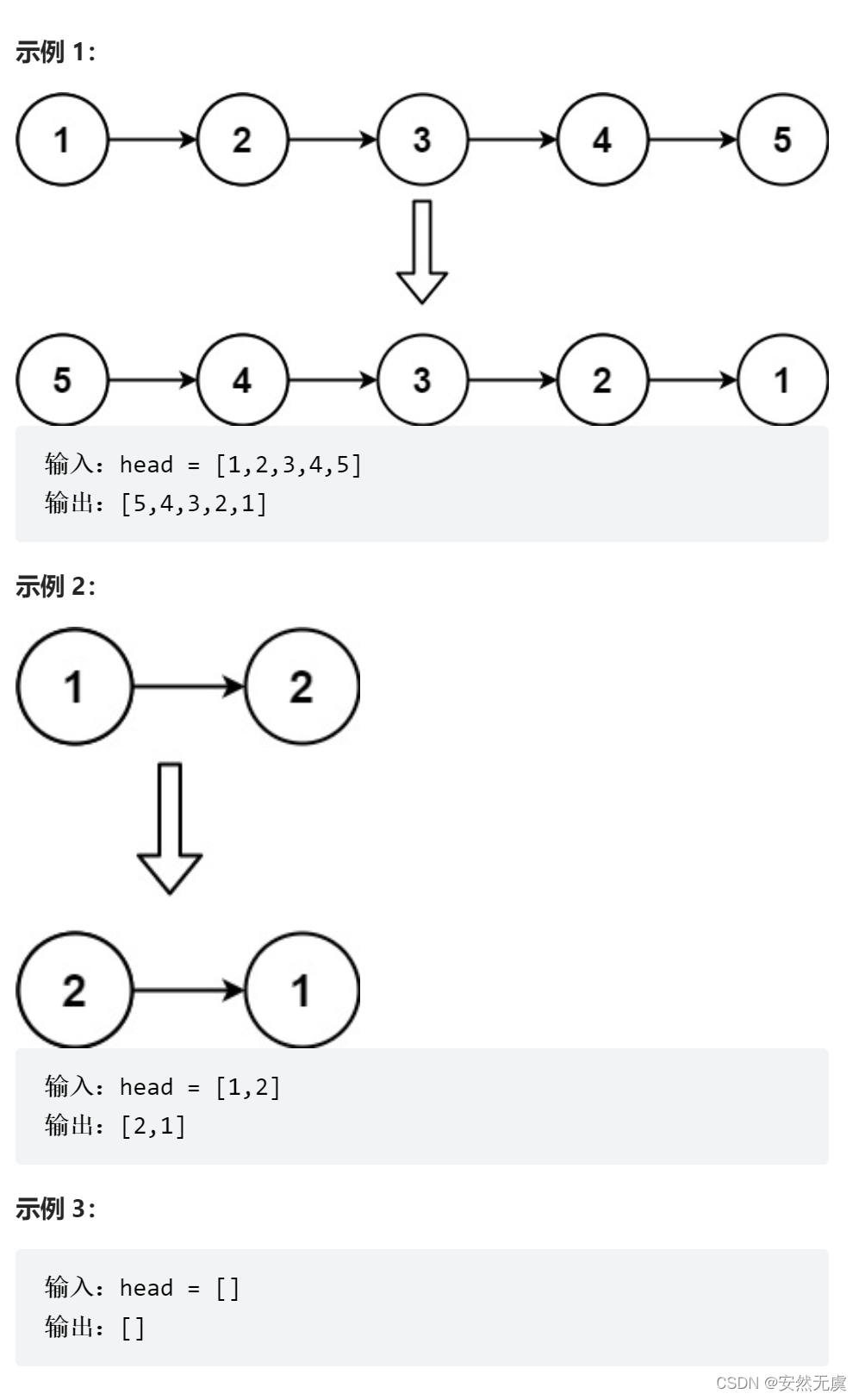 解题思路1:翻指针方向
解题思路1:翻指针方向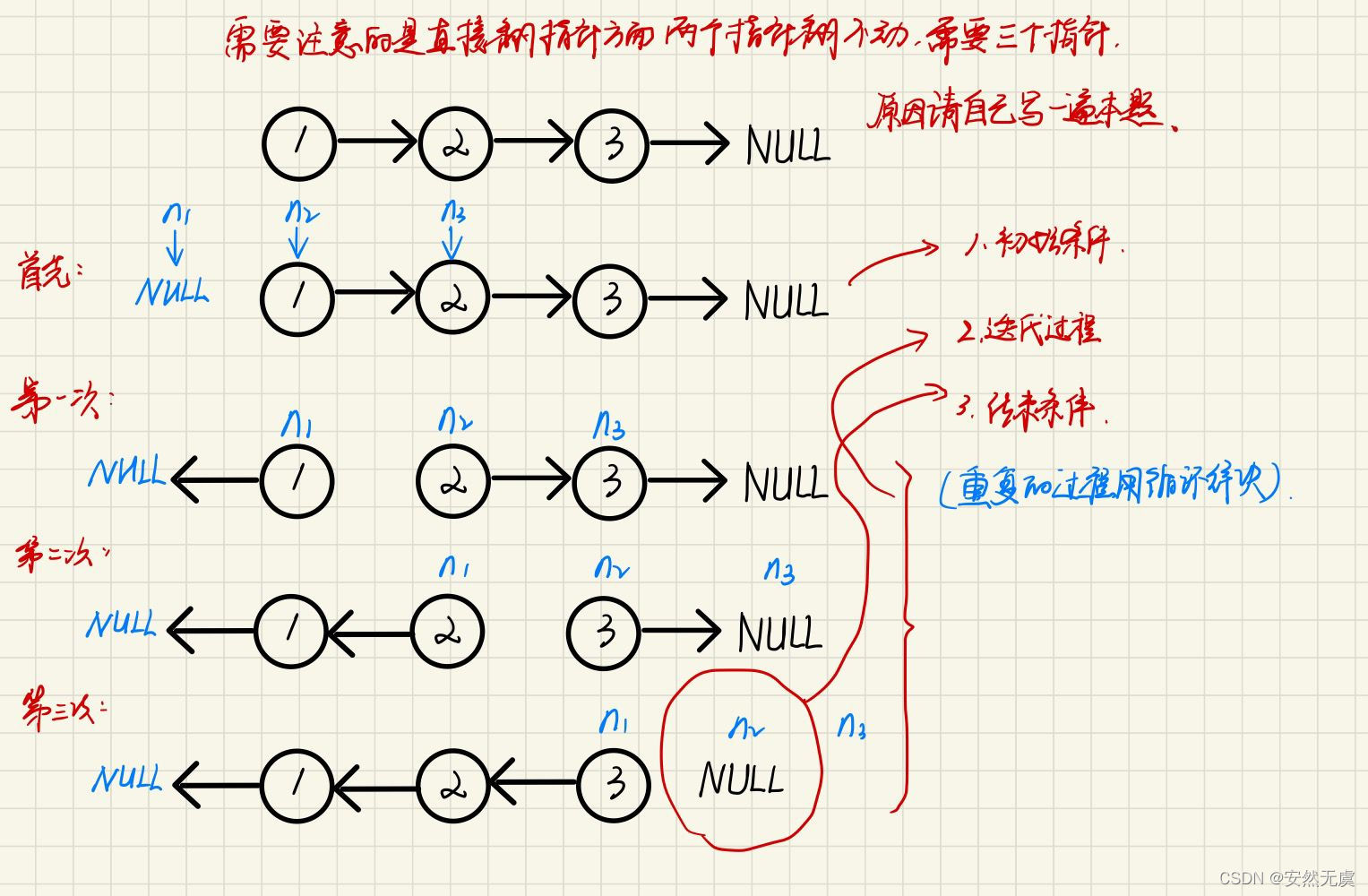 初始代码:
初始代码: 优化后的代码:
优化后的代码: 解题思路2:头插法
解题思路2:头插法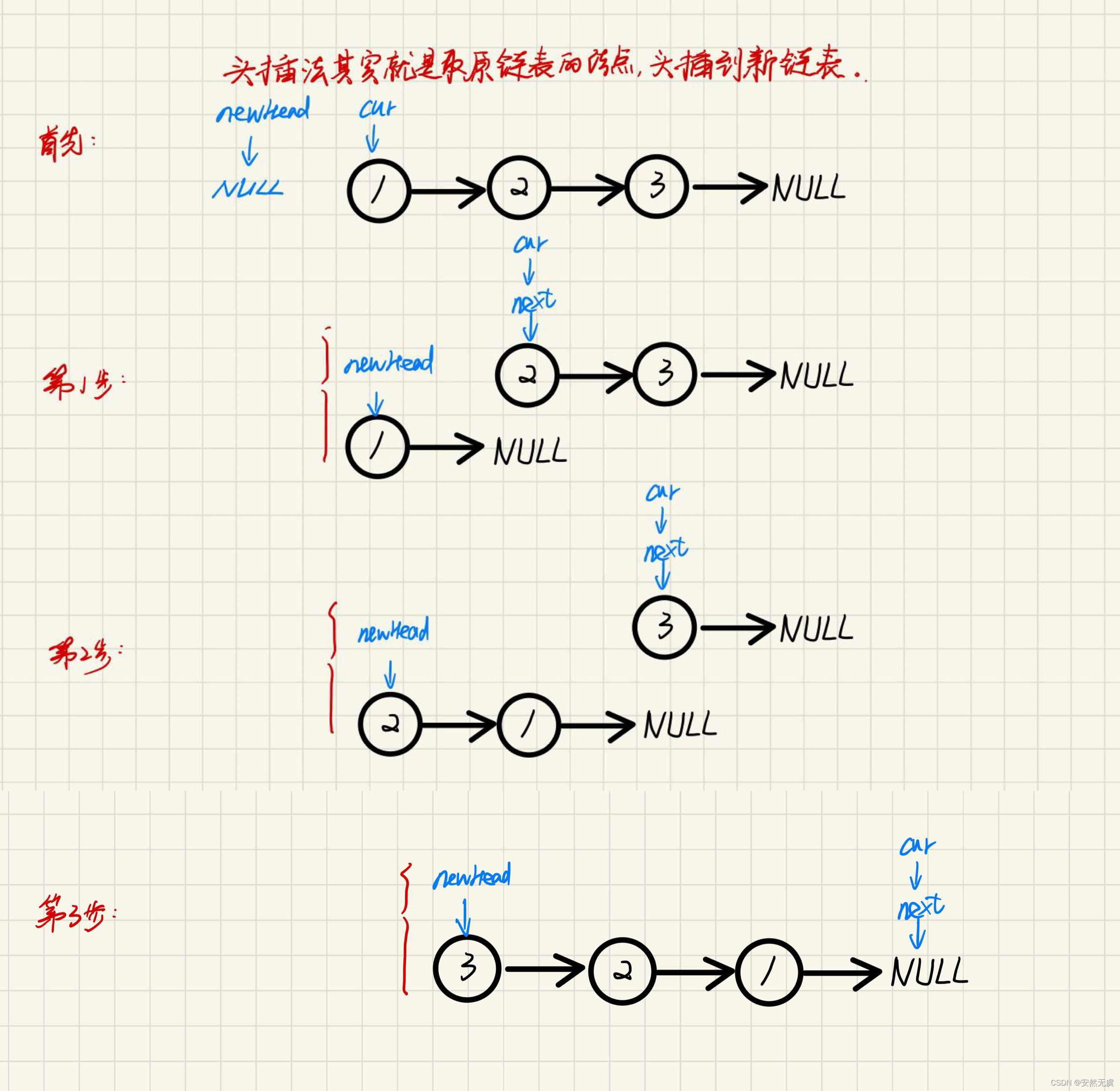 之所以需要多定义一个指针,是因为要保证能找到下一个。
之所以需要多定义一个指针,是因为要保证能找到下一个。

 本题:
本题:
 注意哦,本题时间复杂度不是O(100)
注意哦,本题时间复杂度不是O(100)
 思路分析:
思路分析:


 思路分析:
思路分析:


 解题思路:
解题思路:



 代码执行:
代码执行:
 代码执行:
代码执行:






评论(0)