Java递归寻路实现,你理解递归了吗
哈喽!小伙伴们,好久不见,是不是谈递归色变,递归递归:通俗讲,我们拆分一下,“递”出去,“归”回来,哈哈,正如狂铁所说:“越是困难越是要战胜它”,不如来看看这篇文章,对于小白可能会有新的收获,大牛的话就小kiss了,好,废话不多说,准备好了吗?学习一下基础知识后,我们就来玩起来吧!!!💦

引
看懂这张图,方法调用方法,栈开新栈,递归尾结束要回到main栈,必须一级一级返回,每一次返回都是调用整个方法,调用完成栈被释放,直至回到栈底main递归结束并能够自己画出来,理解递归的运行机制,这是我手画的,不好看,你的呢,还不动起来😏

🆗,到这,如果上面的你都理解了,那么我相信你可以用递归写出 计算 n 的阶乘的程序了,什么,写不出,没有关系,我来补上,一定要理解在栈里运行机制
使用递归计算阶乘
public class Factorial {
public static void main(String[] args) {
Factorial jie = new Factorial ();
System.out.println(jie.f(3));
}
public int f(int n){
if(n == 1){
return 1;
}else {
return n*f(n-1);
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
接下来就可以玩起来了,一个有趣的迷宫问题,假设有如下二维数组表示地图,数字1表示围墙,数字0表示可以走,现在有只小老鼠被困在下标为[1][1]的位置,出口在下标为[6][5]的位置,思考:使用递归如何让小老鼠寻路逃生呢?
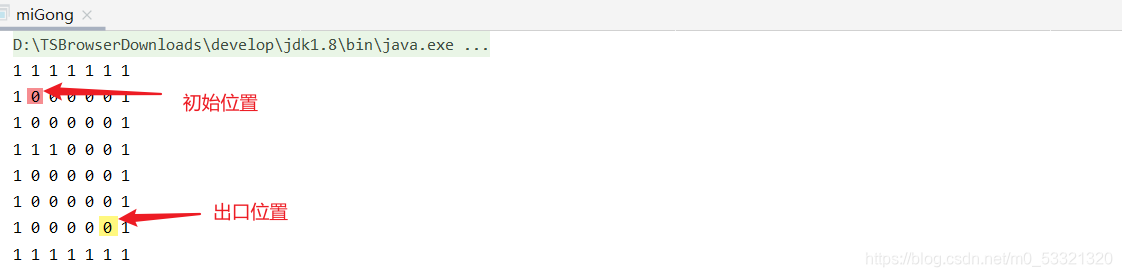
思考过后,脑袋是不是蒙蒙的,不是?那请你喝瓶雪花❄😂

想要玩起来
地图创建
思路
1. 先创建迷宫,用二维数组表示 int[][] map = new int[8][7];
2. 规定 map:0 表示可以走,1表示墙不能走
- 1
- 2
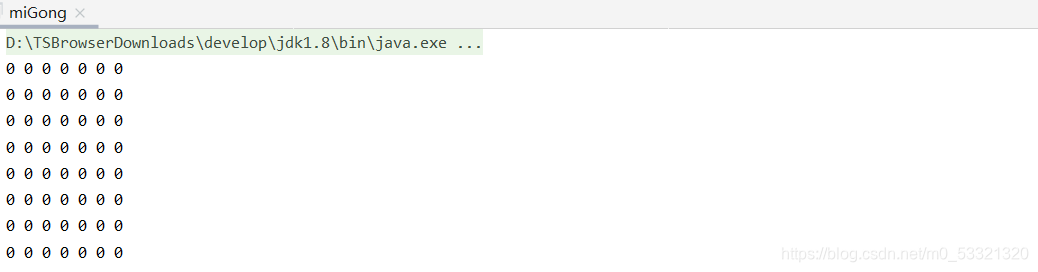
1,打印二维数组
public class miGong {
public static void main(String[] args) {
int[][] map = new int[8][7];
for (int i = 0; i < map.length; i++) {
for (int j = 0; j < map[i].length; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
2,规定墙和可以走的,只需要通过遍历指定行和列,再把两个特别的单独强调,完成
for (int i = 0;i < 7;i++){
map[0][i] = 1;
map[7][i] = 1;
}
for (int i = 0;i < 8;i++){
map[i][0] = 1;
map[i][6] = 1;
}
map[3][1] = 1;
map[3][2] = 1;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
实现效果:

核心
这时就完成了地图,思考如何使用递归寻路呢
开始吧,写一个方法,通过递归来实现寻路,我直接放代码了
- 首先,创建一个类,写
findWay方法,返回值是boolean,三个参数,分别是地图,二维坐标x,y用来确定位置 - 接着,我们判断如果
map[6][5] == 2,就认为小老鼠找到出口了,这点很重要,它是递归回调条件 - 如果
map[6][5] == 2条件为假,说明小老鼠没有找到出口,调用方法时初始化开始坐标,接着map[i][j] = 2;假设可以走通就把坐标的值修改为2,表示老鼠走的痕迹 - 接下来,奇妙的事情发生了,递归就在这里开始了,我们调用自己
findWay传入参数,我们先确定下来小老鼠的行走轨迹,假设是下-右-上-左,我们通过修改数组下标来表示小老鼠的移动,假设上下左右都没能走通,就把坐标值修改为3,表示小老鼠被困死了,返回false,失败,🆗,代码已经完成 - 小伙伴:什么???完成了???

class way{
//使用递归回溯的思想来解决
public boolean findWay(int[][] map,int i,int j){
if(map[6][5] == 2){
return true;
}else{
if(map[i][j] == 0){
//假定可以走通
map[i][j] = 2;
//下-右-上-左
if(findWay(map,i+1,j)){//下
return true;
}else if(findWay(map,i,j+1)){//右
return true;
}else if(findWay(map,i-1,j)){//上
return true;
}else if(findWay(map,i,j-1)){//左
return true;
}else {
map[i][j] = 3;
return false;
}
}else {
return false;
}
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
主函数调用,查看结果:
way f = new way();
f.findWay(map,1,1);
System.out.println("=====找路=====");
for (int i = 0; i < map.length; i++) {
for (int j = 0; j < map[i].length; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
运行代码查看结果:

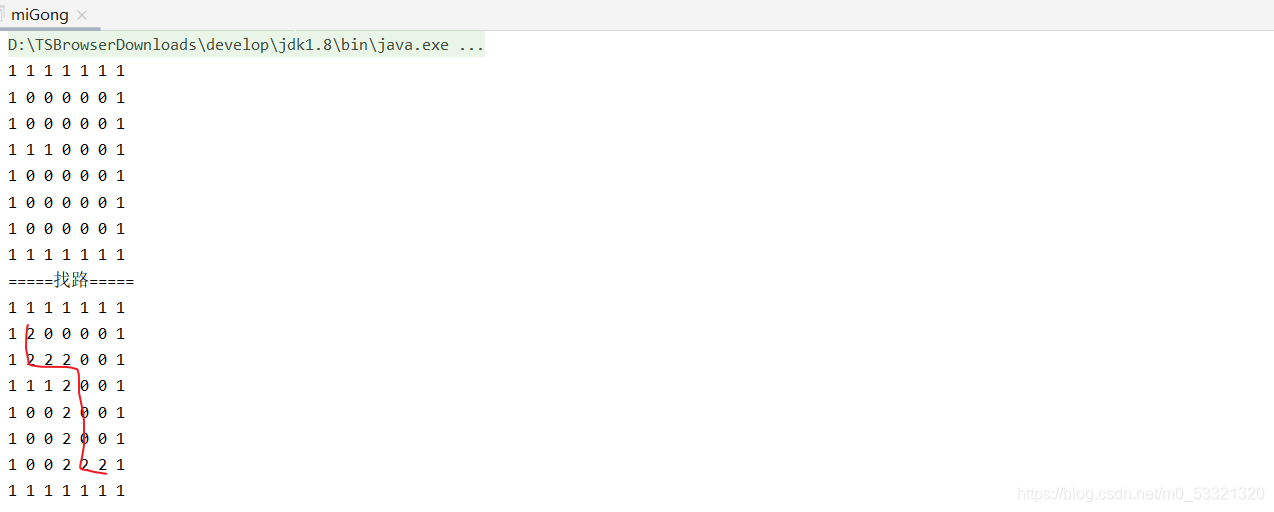
看到成功寻路逃生~~~,是不是还很疑惑

一定要理解透,你也可以设置死路,只要上面的理解了,达到能在脑子里快速回放递归的过程,栈开栈,栈销毁,等等,你就可以随便玩了,之前是不是一直不理解为什么说递归占用空间,谨慎使用,这下就明明白白了,好了,多理解理解,这就是所有内容,感受到递归的魅力了吗?哈哈 是不是很好玩,体会这种思想,感谢观看
完整代码
public class miGong {
public static void main(String[] args) {
//思路
//1.先创建迷宫,用二维数组表示 int[][] map = new int[8][7];
//2.规定 map:0 表示可以走,1表示墙不能走
int[][] map = new int[8][7];
for (int i = 0;i < 7;i++){
map[0][i] = 1;
map[7][i] = 1;
}
for (int i = 0;i < 8;i++){
map[i][0] = 1;
map[i][6] = 1;
}
map[3][1] = 1;
map[3][2] = 1;
//打印
for (int i = 0; i < map.length; i++) {
for (int j = 0; j < map[i].length; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}
way f = new way();
f.findWay(map,1,1);
System.out.println("=====找路=====");
for (int i = 0; i < map.length; i++) {
for (int j = 0; j < map[i].length; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}
}
}
class way{
//使用递归回溯的思想来解决
public boolean findWay(int[][] map,int i,int j){
if(map[6][5] == 2){
return true;
}else{
if(map[i][j] == 0){
//假定可以走通
map[i][j] = 2;
//下-右-上-左
if(findWay(map,i+1,j)){//下
return true;
}else if(findWay(map,i,j+1)){//右
return true;
}else if(findWay(map,i-1,j)){//上
return true;
}else if(findWay(map,i,j-1)){//左
return true;
}else {
map[i][j] = 3;
return false;
}
}else {
return false;
}
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
文章来源: blog.csdn.net,作者:周棋洛ყ ᥱ ᥉,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/m0_53321320/article/details/119888312
- 点赞
- 收藏
- 关注作者


评论(0)