目录

一，牛顿法

二，牛顿法的局限性

三，牛顿下山法

四，割线法

五，抛物线法

一，牛顿法

牛顿法，也叫牛顿迭代法、切线法，是一种迭代求解函数零点的方法。

原理：

令f(x)=0则

取，在一定的范围（x的足够小的邻域）内，x1比x0更接近所求的零点x

根据这个原理，不断的迭代，即可越来越接近x值。

  

   

    

     

    
    

     

      double f(double x)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	return x * x + x * 5 - 8;
     
    
   

    

     

    
    

     

      }
     
    
   

    

     

    
    

     

      double df(double x)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	double eps = 0.001;
     
    
   

    

     

    
    

     
	return (f(x + eps) - f(x)) / eps;
     
    
   

    

     

    
    

     

      }
     
    
   

    

     

    
    

     

      double newton(double x)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	double eps = 0.000001;
     
    
   

    

     

    
    

     
	int times = 100;
     
    
   

    

     

    
    

     
	while (times--) {
     
    
   

    

     

    
    

     
		double x2 = x - f(x) / df(x);
     
    
   

    

     

    
    

     

      		cout << x2 << " ";
     
    
   

    

     

    
    

     
		if (abs(x - x2) < eps)return x2;
     
    
   

    

     

    
    

     

      		x = x2;
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     
	return 0;
     
    
   

    

     

    
    

     

      }
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      int main()
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	double ans = newton(0);
     
    
   

    

     

    
    

     

      	cout << endl << ans << " " << f(ans);
     
    
   

    

     

    
    

     
	return 0;
     
    
   

    

     

    
    

     

      }
     
    
  
 

输出：

1.59968  1.28782  1.27494  1.27492  1.27492
1.27492  3.2081e-12

可以看出收敛很快。

二，牛顿法的局限性

1，牛顿法对于初始值有要求，而且没有很简单的方法去判断一个邻域是否已经足够小。

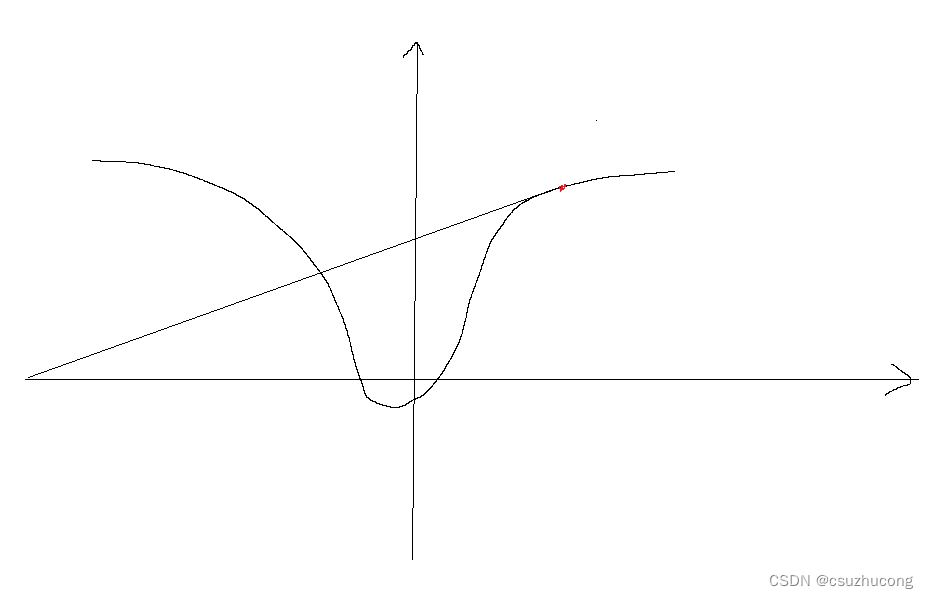
2，序列{x0,x1,x2...}越来越接近x，单调有界必要极限，但是这个极限值是否一定是x，我个人不太确定，但是找到了一个课件中给出了答案：

牛顿法及其收敛性课件

结论是对于单根，|xi - x|平方收敛，但对于有重根的情况只是线性收敛。

如果知道是m重根，则可以改进公式为：

三，牛顿下山法

每取一个新值之前学习率设为1，每次取到新值之后，判断新的函数值是否更接近0，如果不是则降低学习率直到新的函数值更接近0。

在一定程度上降低对于初始值的范围要求。

  

   

    

     

    
    

     

      double newton(double x)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	double eps = 0.000001;
     
    
   

    

     

    
    

     
	int times = 100;
     
    
   

    

     

    
    

     
	double learningRate = 1;
     
    
   

    

     

    
    

     
	while (times--) {
     
    
   

    

     

    
    

     
		double x2 = x - f(x) / df(x)*learningRate;
     
    
   

    

     

    
    

     

      		cout << x2 << " ";
     
    
   

    

     

    
    

     
		if (abs(x - x2) < eps)return x2;
     
    
   

    

     

    
    

     
		if (abs(f(x2)) < abs(f(x))) {
     
    
   

    

     

    
    

     

      			x = x2, learningRate = 1;
     
    
   

    

     

    
    

     

      		} else {
     
    
   

    

     

    
    

     

      			learningRate /= 2;
     
    
   

    

     

    
    

     

      		}
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     
	return 0;
     
    
   

    

     

    
    

     

      }
     
    
  
 

四，割线法

在曲线上取AB两点，求切线AB和x轴的交点C，让BC取代AB进入下一轮迭代，直到两点间距达到精度要求。

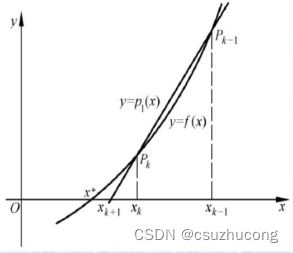
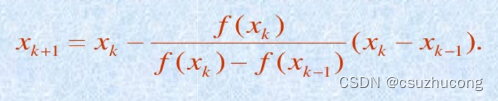
收敛定理：

待补图 

五，抛物线法

待更新

文章来源: blog.csdn.net，作者：csuzhucong，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/nameofcsdn/article/details/124927408