@[TOC](【备战蓝桥杯】 算法·每日一题（详解+多解）-- day11)

✨博主介绍

🌊 作者主页：苏州程序大白

🌊 作者简介：🏆CSDN人工智能域优质创作者🥇，苏州市凯捷智能科技有限公司创始之一，目前合作公司富士康、歌尔等几家新能源公司

💬如果文章对你有帮助，欢迎关注、点赞、收藏

💅 有任何问题欢迎私信，看到会及时回复
💅关注苏州程序大白，分享粉丝福利

前言

本文总结算法中涉及图的最短路径可能用到的算法，主要分为两大类，一类是单源最短路径，即计算一个给定的顶点到其他顶点的最短路径，一类是多源最短路径，即计算顶点两两之间的最短路径。

单源最短路径：

• Dijkstra 算法
• Bellman-Ford 算法
• SPFA 算法

多源最短路径：

• Floyd 算法
• Johnson 全源最短路径算法

Dijkstra 算法

Dijkstra 算法用来计算边权均非负的单源最短路径算法。

流程

算法输入图、起点

将顶点分成两个集合：已确定最短路长度的点集（记为S集合）的和未确定最短路长度的点集（记为T 集合）。一开始所有的点都属于T集合。

初始化 dis(s)=0，其他点到源点的距离均为∞ 。

然后重复这些操作：

从T集合中，选取当前最短路长度最小的点，移到S集合中。
对那些刚刚被加入S集合的结点的所有出边执行松弛操作。
直到T集合为空，算法结束。

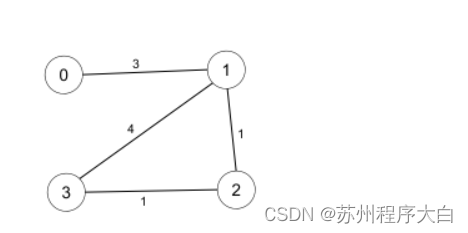
以下图为例，计算流程展现在表格中（以-1代表无穷大，*代表顶点已确定最短路）。


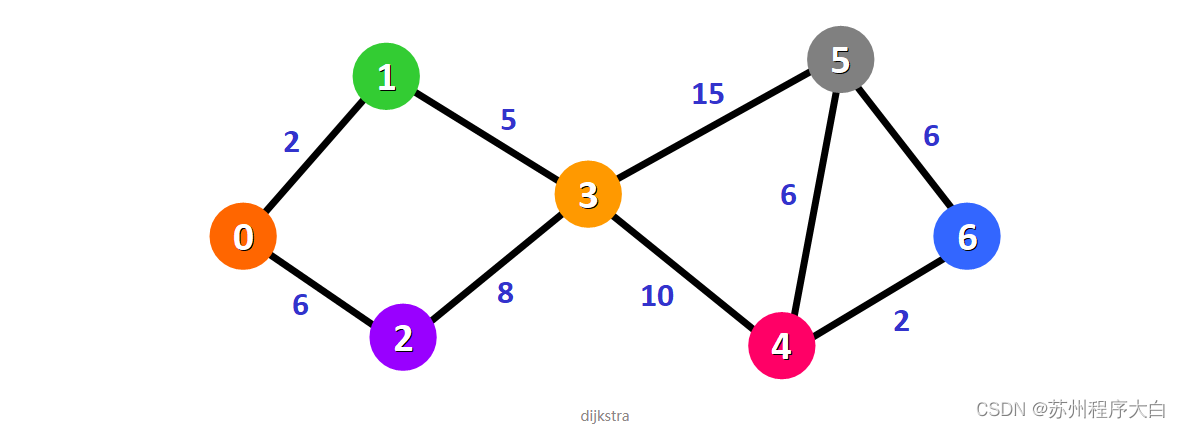
对此表稍做解释：

• 初始只有源点0的距离已知是0，其他都是无穷大（-1）。
• 0的邻居1和2均为被访问过，于是加入，并更新最短路距离，此轮中0的最短路距离最小，顶点0加入 S。
• 由顶点1和2可以延伸到顶点3，更新3的最短路为7，此轮1的最短路距离最小，顶点1加入 S。
• 以此类推，直到所有顶点加入 S。

网络延迟时间

您将获得一个n节点网络，标记为从1到n。还给出times了作为有向边的行进时间列表，其中是源节点，是目标节点，是信号从源传输到目标所需的时间。times[i] = (ui, vi, wi)uiviwi

我们将从给定节点发送一个信号k。返回所有n节点接收信号所需的时间。如果所有n节点都无法接收到信号，则返回-1。

示例 1：

输入： times = [[2,1,1],[2,3,1],[3,4,1]]，n = 4，k = 2
输出： 2

示例 2：
输入： times = [[1,2,1]]，n = 2，k = 1
输出： 1

示例 3：
输入： times = [[1,2,1]]，n = 2，k = 2
输出： -1

约束：

· 1 <= k <= n <= 100
· 1 <= times.length <= 6000
· times[i].length == 3
· 1 <= ui, vi <= n
· ui != vi
· 0 <= wi <= 100
· 所有的对都是独一无二的。（即，没有多重边。）(ui, vi)

解题思路

class Solution 
{
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) 
    {
        int INF = 1e9;
        unordered_map<int, vector<pair<int, int>>> adjvex;
        for (auto v : times) {
            adjvex[v[0]].push_back({v[1], v[2]});
        }

        vector<int> dist(n + 1, INF);
        dist[k] = 0;
        priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>> > minHeap;
        minHeap.push({0, k});
        while (!minHeap.empty()) {
            auto [d, x] = minHeap.top();
            minHeap.pop();
            if (d > dist[x] || dist[x] == INF)
                continue;
            for (auto [y, cost] : adjvex[x]) {
                if (dist[x] + cost < dist[y]) {
                    dist[y] = dist[x] + cost;
                    minHeap.push({dist[y], y});
                }
            }
        }
        int res = *max_element(dist.begin() + 1, dist.end());  
        return (res != INF ? res : -1);
    }   
};

Bellman-Ford 算法

Bellman-Ford 可以处理有负权边的单源最短路径问题。

流程

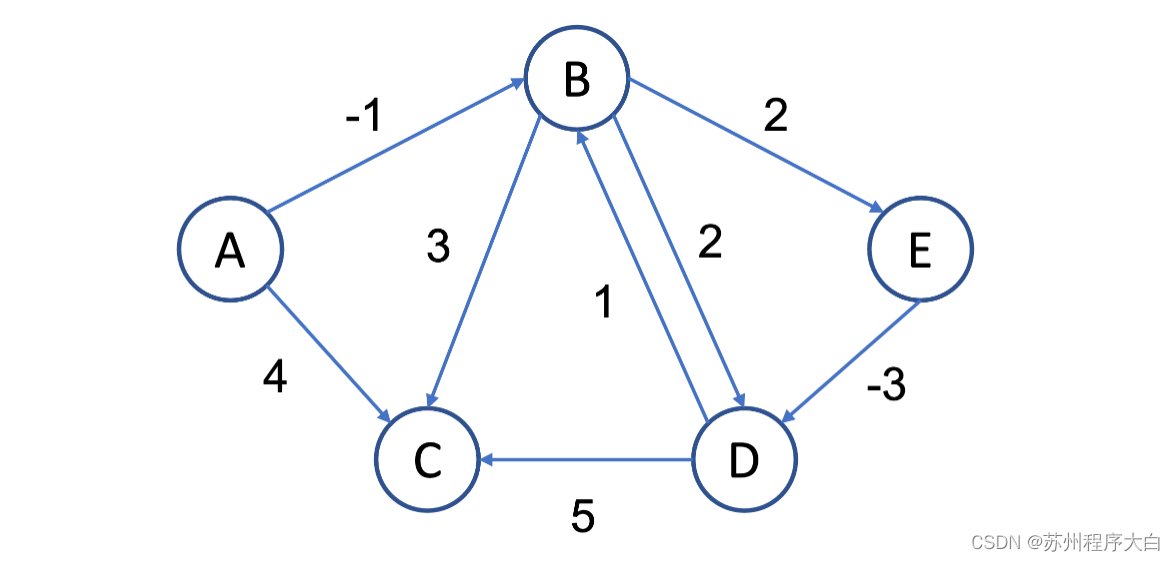
将下方图中的所有边，遍历 n-1 次。对于边(u,v,w)，若dist[u]+w<dist[v]，则更新dist[v]。

• 为什么要遍历所有边：第 i次遍历，其实是确定其他点分别到源点的最短路径上，第i 个顶点是谁，也可以说是经过的第i 条边是谁。
• 为什么要遍历n-1 次：在每个顶点到源点的最短路径上，顶点数最多为n 个，除非有负环，所以最多只需要遍历n-1次(第一个顶点已经确定下来了)，就可以确定所有顶点的最短路径。

若已经经过n-1 次遍历，再次遍历时仍有边能进行松弛，则说明图中有负权值的环路。因为此时进行松弛的路径已经包含了最少 n条边n + 1个点，这说明图中一定形成了环路。去除正权值环路会使路径减小，因此在此最短路径中一定不存在正权值环路，此环路一定为负。 在完成核心算法后再次遍历尝试松弛即可检验出该图是否含有负权值环路。

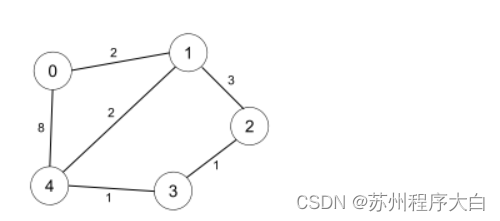
下面图里有5个点8条边，需要遍历4轮。留给大家自行计算。

K 站内最便宜的航班

有些n城市通过一定数量的航班相连。您将获得一个数组flights，其中表示从一个城市到另一个城市的航班为cost。flights[i] = [fromi, toi,pricei]fromitoipricei

还给您三个整数src、dst和k，返回最便宜的价格从src到dst最多k停止。如果没有这样的路线，请返回。-1

示例 1：

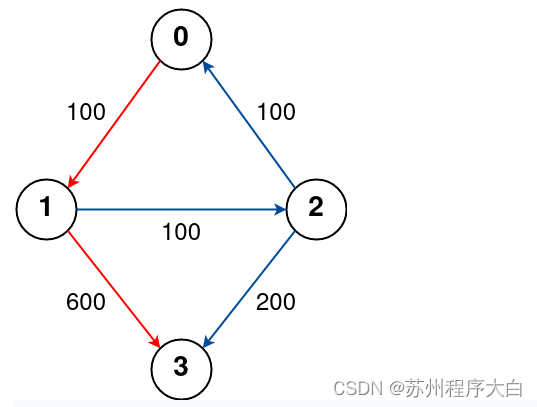
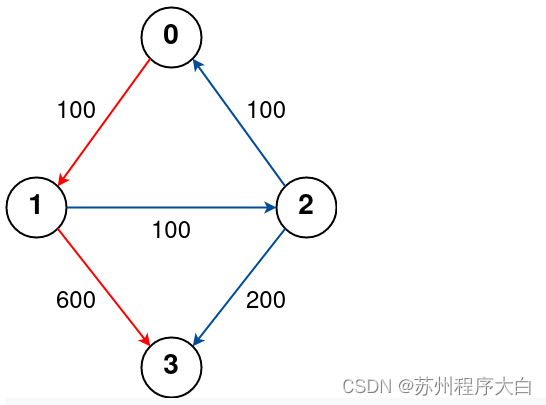
输入： n = 4，航班 = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1
输出： 700
解释：
图表如上所示。
从城市 0 到 3 最多停靠 1 站的最佳路径用红色标记，成本为 100 + 600 = 700。
请注意，通过城市 [0,1,2,3] 的路径更便宜但无效，因为它使用 2 个停靠点。

示例 2：

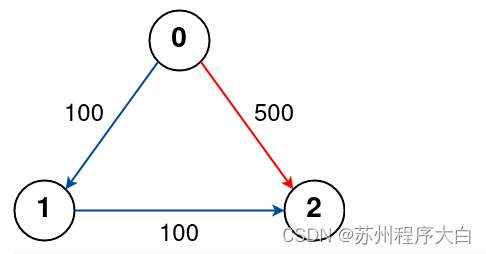
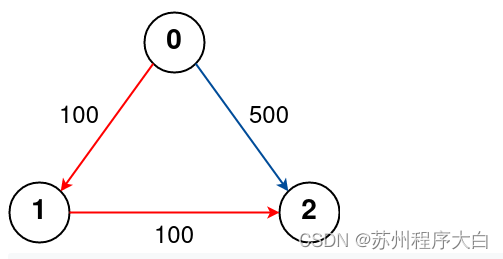
输入： n = 3, flight = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
输出： 200
解释：
图表如上所示。
从城市 0 到 2 最多停靠 1 站的最佳路径用红色标记，成本为 100 + 100 = 200。

示例 3：

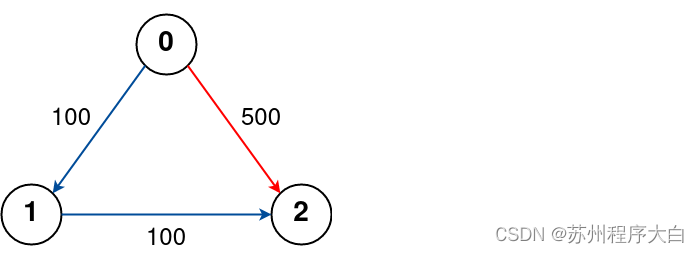
输入： n = 3, flight = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
输出： 500
解释：
图表如上所示。
从城市 0 到 2 没有停靠的最佳路径用红色标记，费用为 500。

约束：

· 1 <= n <= 100
· 0 <= flights.length <= (n * (n - 1) / 2)
· flights[i].length == 3
· 0 <= fromi, toi < n
· fromi != toi
· 1 <= pricei <= 104
· 两个城市之间不会有多个航班。
· 0 <= src, dst, k < n
· src != dst

解题思路

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        vector<int> dp(n, 0x3f3f3f3f);
        dp[src] = 0;
        while(1+k--){
            vector<int> next = dp;
            for(auto& x: flights) next[x[1]] = min(next[x[1]], dp[x[0]] + x[2]);
            dp = move(next);
        }
        return dp[dst] == 0x3f3f3f3f ? -1 : dp[dst];
    }
};

SPFA算法

SPFA算法是Shortest Path Faster Algorithm的缩写。在Bellman Ford算法中，我们有很多判断是否松弛的操作，很多时候我们并不需要那么多无用的松弛操作。我们很显然能观察到，只有上一次被松弛的结点，所连接的边，才有可能引起下一次的松弛操作。那么我们用队列来维护“哪些结点可能会引起松弛操作”，就能只访问必要的边了。

SPFA 也可以用于判断点S是否能抵达一个负环，只需记录最短路经过了多少条边，当经过了至少N条边时，说明点S可以抵达一个负环。

K 站内最便宜的航班

有些n城市通过一定数量的航班相连。您将获得一个数组flights，其中表示从一个城市到另一个城市的航班为cost。flights[i] = [fromi, toi, pricei]fromitoipricei

还给您三个整数src、dst和k，返回最便宜的价格从src到dst最多k停止。如果没有这样的路线，请返回。 -1。

示例 1：

输入： n = 4，航班 = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1
输出： 700
解释：
图表如上所示。
从城市 0 到 3 最多停靠 1 站的最佳路径用红色标记，成本为 100 + 600 = 700。
请注意，通过城市 [0,1,2,3] 的路径更便宜但无效，因为它使用 2 个停靠点。

示例 2：

输入： n = 3, flight = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
输出： 200
解释：
图表如上所示。
从城市 0 到 2 最多停靠 1 站的最佳路径用红色标记，成本为 100 + 100 = 200。

示例 3：

输入： n = 3, flight = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
输出： 500
解释：
图表如上所示。
从城市 0 到 2 没有停靠的最佳路径用红色标记，费用为 500。

约束：

· 1 <= n <= 100
· 0 <= flights.length <= (n * (n - 1) / 2)
· flights[i].length == 3
· 0 <= fromi, toi < n
· fromi != toi
· 1 <= pricei <= 104
· 两个城市之间不会有多个航班。
· 0 <= src, dst, k < n
· src != dst

解题思路

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        vector<int> dp(n, 0x3f3f3f3f);
        vector<vector<int> > e(n);
        queue<int> q;
        int sq;

        for(auto& x: flights) e[x[0]].push_back((x[1] << 16) + x[2]);
        dp[src] = 0;
        q.push(src);
        while(1+k-- && (sq = q.size())){
            vector<bool> vis(n);
            vector<int> cpy = dp;
            while(sq--){
                int now = q.front();
                for(auto x: e[now]){
                    int next = x>>16, v = x&0xffff;
                    cpy[next] = std::min(cpy[next], dp[now] + v);
                    if(vis[next]) continue;
                    vis[next] = 1;
                    q.push(next);
                }
                q.pop();
            }
            dp = move(cpy);
        }
        return dp[dst] == 0x3f3f3f3f ? -1 : dp[dst];
    }
};

具有最大概率的路径

您将获得一个 n 节点的无向​​加权图（索引为 0），由边列表表示，其中edges[i] = [a, b] 连接节点的无向​​边 a 和b 遍历该边的成功概率 succProb[i] 。

给定两个节点start 和end ，找到从start 到 成功概率最大的路径，end 并返回其成功概率。

如果没有从 start to 的路径end ，则返回 0 。如果您的答案与正确答案最多相差1e-5 ，您的答案将被接受。

示例 1：

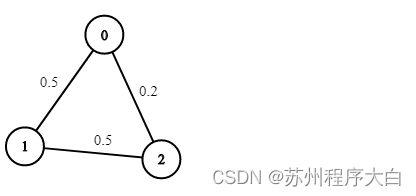
输入： n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出： 0.25000
解释： 从开始到结束有两条路径，一条成功概率 = 0.2，另一条成功概率为 0.5 * 0.5 = 0.25。

示例 2：

输入： n = 3，边 = [[0,1]，[1,2]，[0,2]]，succProb = [0.5,0.5,0.3]，开始 = 0，结束 = 2
输出： 0.30000

示例 3：

输入： n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
输出： 0.00000
解释： 0 和 2 之间没有路径。

 约束：

· 2 <= n <= 10^4
· 0 <= start, end < n
· start != end
· 0 <= a, b < n
· a != b
· 0 <= succProb.length == edges.length <= 2*10^4
· 0 <= succProb[i] <= 1
· 每两个节点之间最多有一条边。

解题思路

class Solution {
public:
    vector<vector<pair<int, double> > > g;
    vector<double> dist;
    vector<bool> st;
    double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
        g.resize(n);
        dist.resize(n, 0.0);
        st.resize(n, false);
        for(int i = 0; i < edges.size(); i++) {
            int x = edges[i][0], y = edges[i][1];
            double z = succProb[i];
            g[x].push_back({y, z});
            g[y].push_back({x, z});
        }
        spfa(start);
        return dist[end];
    }
    
    void spfa(int s){
        dist[s] = 1;
        queue<int> q;
        q.push(s);
        st[s] = true;
        while (!q.empty()) {
            int t = q.front();
            q.pop();
            st[t] = false;
            for (const auto &[v, w]: g[t]) {
                if (dist[v] < dist[t] * w) {
                    dist[v] = dist[t] * w;
                    if (!st[v])
                        q.push(v);
                }
            }
        }
    }
};

Floyd 算法

Floyd 算法是用来求任意两个节点之间的最短路的多源最短路径算法，可以正确处理有向图或负权的最短路径问题，但要求最短路存在（无负环）。

Floyd 算法是一个动态规划算法，目标是求出任意节点i到任意节点 j之间的最短距离。从动态规划的角度来说，我们需要归纳问题的子问题：从任意节点i到任意节点i的最短路径不外乎2种可能，一种是直接从i到 ，另一种是从i经过一个及以上的节点k到j。因此，若假设 Dis(i,j)为节点i到节点k的最短路径的距离，那么动态转移方程可以写成

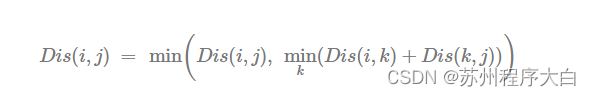
Dis(i,j)初始化成i和j之间的直接距离或者无穷大。核心代码：

for (int k = 0; k < n; k++) {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            dis[i][j] = std::min(dis[i][j], dis[i][k] + dis[k][j]);
        }
    }
}

找到阈值距离内邻居数量最少的城市

有从到n编号的城市。给定数组where表示城市和之间的双向加权边缘，并给定整数。0n-1edgesedges[i] = [fromi, toi, weighti]fromitoidistanceThreshold

返回通过某条路径可达且距离最大 distanceThreshold的城市数量最少的城市，如果有多个这样的城市，则返回数量最多的城市。

请注意，连接城市i和j的路径的距离等于沿该路径的边权重之和。

示例 1：

输入： n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
输出： 3
解释：上图描述了图表。
每个城市距离Threshold = 4 的相邻城市是：
城市 0 -> [城市 1，城市 2]
城市 1 -> [城市 0、城市 2、城市 3]
城市 2 -> [城市 0、城市 1、城市 3]
城市 3 -> [城市 1，城市 2]
城市 0 和 3 在 distanceThreshold = 4 处有 2 个相邻城市，但我们必须返回城市 3，因为它的数量最多。

示例 2：

输入： n = 5，边 = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[ 3,4,1]], distanceThreshold = 2
输出： 0
解释：上图描述了图形。
每个城市距离Threshold = 2 的相邻城市是：
城市 0 -> [城市 1]
城市 1 -> [城市 0，城市 4]
城市 2 -> [城市 3, 城市 4]
城市 3 -> [城市 2，城市 4]
城市 4 -> [城市 1、城市 2、城市 3]
城市 0 在 distanceThreshold = 2 处有 1 个相邻城市。

约束：

2 <= n <= 100
1 <= edges.length <= n * (n - 1) / 2
edges[i].length == 3
0 <= fromi < toi < n
1 <= weighti, distanceThreshold <= 10^4
所有对都是不同的。(fromi, toi)

解题思路

class Solution {
public:
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        const int INF = 0x3f3f3f3f;
        int dist[n][n];
        memset(dist,INF,sizeof(dist));
        for(int i=0;i<n;i++)
        dist[i][i]=0;
        for(int i=0;i<edges.size();i++){
            dist[edges[i][0]][edges[i][1]]=edges[i][2];
            dist[edges[i][1]][edges[i][0]]=edges[i][2];
        }
        for(int k=0;k<n;k++){
            for(int i=0;i<n;i++){
                for(int j=0;j<n;j++){
                    dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j]);
                }
            }
        }
        int id=-1, minCnt=INF;
        for(int i=0;i<n;i++){
            int cnt=0;
            for(int j=0;j<n;j++){
                if(dist[i][j]<=distanceThreshold)
                    cnt++;
            }
            if(cnt<=minCnt){
                minCnt=cnt;
                id=i;
            }
        }
        return id;
    }
};

Johnson 全源最短路径算法

任意两点间的最短路可以通过枚举起点，跑 nn 次 Bellman-Ford 算法解决，时间复杂度是 O(n^2m)O(n 2 m) 的，也可以直接用 Floyd 算法解决，时间复杂度为 O(n^3)O(n 3 ) 。

注意到堆优化的 Dijkstra 算法求单源最短路径的时间复杂度比 Bellman-Ford 更优，如果枚举起点，跑 nn 次 Dijkstra 算法，就可以在 O(nm\log m)O(nmlogm) （本文中的 Dijkstra 采用 priority_queue 实现，下同）的时间复杂度内解决本问题，比上述跑 nn 次 Bellman-Ford 算法的时间复杂度更优秀，在稀疏图上也比 Floyd 算法的时间复杂度更加优秀。

但 Dijkstra 算法不能正确求解带负权边的最短路，因此我们需要对原图上的边进行预处理，确保所有边的边权均非负。

一种容易想到的方法是给所有边的边权同时加上一个正数 xx ，从而让所有边的边权均非负。如果新图上起点到终点的最短路经过了 kk 条边，则将最短路减去 kxkx 即可得到实际最短路。

但这样的方法是错误的。考虑下图：

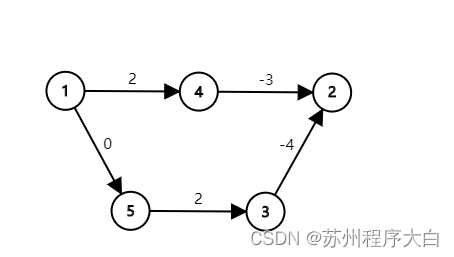
1→2 的最短路为 1 \to 5 \to 3 \to 21→5→3→2，长度为 -2−2。

但假如我们把每条边的边权加上 55 呢？

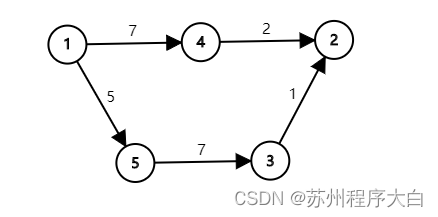
新图上 1 \to 21→2 的最短路为 1 \to 4 \to 21→4→2 ，已经不是实际的最短路了。

Johnson 算法则通过另外一种方法来给每条边重新标注边权。

我们新建一个虚拟节点（在这里我们就设它的编号为 00 ）。从这个点向其他所有点连一条边权为 00 的边。

接下来用 Bellman-Ford 算法求出从 00 号点到其他所有点的最短路，记为 h_ih i 。

假如存在一条从 uu 点到 vv 点，边权为 ww 的边，则我们将该边的边权重新设置为 w+h_u-h_vw+h u −h v 。

接下来以每个点为起点，跑 nn 轮 Dijkstra 算法即可求出任意两点间的最短路了。

容易看出，该算法的时间复杂度是 O(nm\log m)O(nmlogm) 。

Q：那这么说，Dijkstra 也可以求出负权图（无负环）的单源最短路径了？

A：没错。但是预处理要跑一遍 Bellman-Ford，还不如直接用 Bellman-Ford 呢。

正确性证明

为什么这样重新标注边权的方式是正确的呢？

在讨论这个问题之前，我们先讨论一个物理概念——势能。

诸如重力势能，电势能这样的势能都有一个特点，势能的变化量只和起点和终点的相对位置有关，而与起点到终点所走的路径无关。

势能还有一个特点，势能的绝对值往往取决于设置的零势能点，但无论将零势能点设置在哪里，两点间势能的差值是一定的。

接下来回到正题。

在重新标记后的图上，从 ss 点到 tt 点的一条路径 s \to p_1 \to p_2 \to \dots \to p_k \to ts→p 1→p 2 →⋯→p k→t 的长度表达式如下：
(w(s,p_1)+h_s-h_{p_1})+(w(p_1,p_2)+h_{p_1}-h_{p_2})+ \dots +(w(p_k,t)+h_{p_k}-h_t)(w(s,p 1)+h s−h p 1)+(w(p 1,p 2)+h p 1−hp 2)+⋯+(w(p k,t)+h p k−h t)
化简后得到：
w(s,p_1)+w(p_1,p_2)+ \dots +w(p_k,t)+h_s-h_tw(s,p 1)+w(p 1,p 2)+⋯+w(p k,t)+h s −h t无论我们从 ss 到 tt 走的是哪一条路径， h_s-h_th s −h t的值是不变的，这正与势能的性质相吻合！为了方便，下面我们就把 h_ihi称为 ii 点的势能。

上面的新图中 s \to ts→t 的最短路的长度表达式由两部分组成，前面的边权和为原图中 s \to ts→t 的最短路，后面则是两点间的势能差。因为两点间势能的差为定值，因此原图上 s \to ts→t 的最短路与新图上 s \to ts→t 的最短路相对应。

到这里我们的正确性证明已经解决了一半——我们证明了重新标注边权后图上的最短路径仍然是原来的最短路径。接下来我们需要证明新图中所有边的边权非负，因为在非负权图上，Dijkstra 算法能够保证得出正确的结果。

根据三角形不等式，新图上任意一边 (u,v)(u,v) 上两点满足： h_v \leq h_u + w(u,v)h v ≤h u +w(u,v) 。这条边重新标记后的边权为 w’(u,v)=w(u,v)+h_u-h_v \geq 0w ′ (u,v)=w(u,v)+h u −h v ≥0 。这样我们证明了新图上的边权均非负。

至此，我们就证明了 Johnson 算法的正确性。

解题思路

#include <cstring>
#include <iostream>
#include <queue>
#define INF 1e9
using namespace std;
struct edge {
  int v, w, next;
} e[10005];
struct node {
  int dis, id;
  bool operator<(const node& a) const { return dis > a.dis; }
  node(int d, int x) { dis = d, id = x; }
};
int head[5005], vis[5005], t[5005];
int cnt, n, m;
long long h[5005], dis[5005];
void addedge(int u, int v, int w) {
  e[++cnt].v = v;
  e[cnt].w = w;
  e[cnt].next = head[u];
  head[u] = cnt;
}
bool spfa(int s) {
  queue<int> q;
  memset(h, 63, sizeof(h));
  h[s] = 0, vis[s] = 1;
  q.push(s);
  while (!q.empty()) {
    int u = q.front();
    q.pop();
    vis[u] = 0;
    for (int i = head[u]; i; i = e[i].next) {
      int v = e[i].v;
      if (h[v] > h[u] + e[i].w) {
        h[v] = h[u] + e[i].w;
        if (!vis[v]) {
          vis[v] = 1;
          q.push(v);
          t[v]++;
          if (t[v] == n + 1) return false;
        }
      }
    }
  }
  return true;
}
void dijkstra(int s) {
  priority_queue<node> q;
  for (int i = 1; i <= n; i++) dis[i] = INF;
  memset(vis, 0, sizeof(vis));
  dis[s] = 0;
  q.push(node(0, s));
  while (!q.empty()) {
    int u = q.top().id;
    q.pop();
    if (vis[u]) continue;
    vis[u] = 1;
    for (int i = head[u]; i; i = e[i].next) {
      int v = e[i].v;
      if (dis[v] > dis[u] + e[i].w) {
        dis[v] = dis[u] + e[i].w;
        if (!vis[v]) q.push(node(dis[v], v));
      }
    }
  }
  return;
}
int main() {
  ios::sync_with_stdio(false);
  cin >> n >> m;
  for (int i = 1; i <= m; i++) {
    int u, v, w;
    cin >> u >> v >> w;
    addedge(u, v, w);
  }
  for (int i = 1; i <= n; i++) addedge(0, i, 0);
  if (!spfa(0)) {
    cout << -1 << endl;
    return 0;
  }
  /*
  for(int i=1;i<=n;i++)
   cout<<h[i]<<' ';
  cout<<endl;
  */
  for (int u = 1; u <= n; u++)
    for (int i = head[u]; i; i = e[i].next) e[i].w += h[u] - h[e[i].v];
  for (int i = 1; i <= n; i++) {
    dijkstra(i);
    long long ans = 0;
    for (int j = 1; j <= n; j++) {
      if (dis[j] == INF)
        ans += j * INF;
      else
        ans += j * (dis[j] + h[j] - h[i]);
    }
    cout << ans << endl;
  }
  return 0;
}

💫点击直接资料领取💫

❤️关注苏州程序大白公众号❤️

👇 👇👇