一、问题来源

问题来自帮朋友做的一个题，如下所示：

我主要做了：

• 可视化捕食者和被捕食者数量随时间变换情况；
• 利用 numpy 的 polyfit、poly1d 拟合数据点分别得到两个多项式方程；
• scipy求导并代入值计算；
• 等式两边的输入都有了，用多元线性回归（fit_intercept=False，不要截距）拟合数据，分别估计方程两个参数；
• 最终得到拟合的 a，b，c，d 的值；

二、引言

捕食者和被捕食者模型（Predator-Prey Model），这是生态学中非常经典的一个模型。

假设一个生态系统中有两个物种，其中一个为食草动物，两者分别构成了捕食者和被捕食者。以兔子和狐狸为例：

• $x(t)$ : 狐狸的数量随时间变换的函数
• $y(t)$：兔子的数量随时间变换的函数

如果没有兔子，狐狸的数量会因为缺少食物而减少：
$$\frac{\mathrm{d}x}{\mathrm{d}t}=-ax,a>0$$

事实上，生态系统中的兔子和狐狸存在一种互动关系，兔子的数量会因为狐狸数量的增加而减少，狐狸的数量也会因为兔子数量的减少而减少，两者之始至终都相互影响。我们用正比于两者数量的积来表示这种互动关系, 所以更精确的模型可以这样写：

$$\frac{\mathrm{d}x}{\mathrm{d}t}=-ax+bxy$$

现在考虑兔子的数量，如果没有狐狸，并且假设自然资源、空间充足，那么兔子会呈现指数式增长：

$$\frac{\mathrm{d}y}{\mathrm{d}t}=dy,d>0$$

事实上，兔子的数量会随着狐狸数量的增加而减少，这种减少体现在两种生物的互动过程中。

结合之前的分析，我们可以得到一个综合的微分方程组：

$$\frac{\mathrm{d}x}{\mathrm{d}t}=-ax+bxy$$

$$\frac{\mathrm{d}y}{\mathrm{d}t}=dy-cxy$$

捕食者和被捕食者模型，这个著名的方程组也叫做 Lotka-Volterra predator-prey model。

三、Python分析

可视化捕食者和被捕食者模型随时间变换情况：

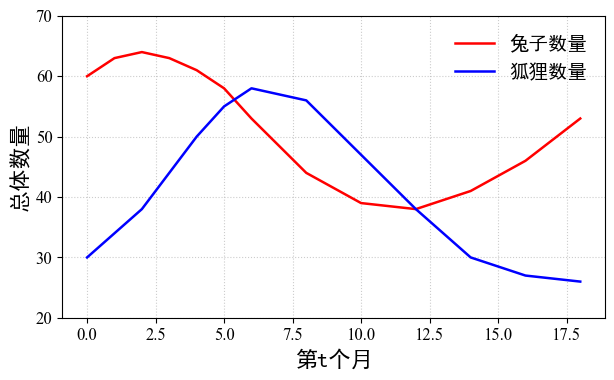
利用 numpy 的 polyfit、poly1d 拟合数据点，分别得到两个多项式方程。

scipy求导并代入值计算，等式两边的输入都有了，用多元线性回归（fit_intercept=False，不要截距）拟合数据，可以分别估计方程两个参数；最终得到拟合的 a，b，c，d 的值。

文章来源: yetingyun.blog.csdn.net，作者：叶庭云，版权归原作者所有，如需转载，请联系作者。

原文链接：yetingyun.blog.csdn.net/article/details/124534372