有噪信道编码详解

截止目前，没有一种码能够达到香农第二定理的极限

因此，在给定的信息传输情况下，是允许存在一定的出错概率，仅做如下要求：

1.码长尽量短

2.信息率尽量大

3.揪检错能力尽量大

4.编码规律尽量简单

5.与信道的差错统计特性尽量匹配

分组码

将长度为k位的信息码组变换成n长（n>k）的码字，其中码字的k位称位信息位，n-k位称为检验位或监督位。由个信息码组所编成的个码字的集合称为分组码。

编码效率

R=k/n，表示码字中信息位所占的比重，称为编码效率或编码速率，表示了信道的利用率。

系统码与非系统码

（n，k）分组码，只有在那k位校验码在n长字码前（或后）k位，才称为系统码。

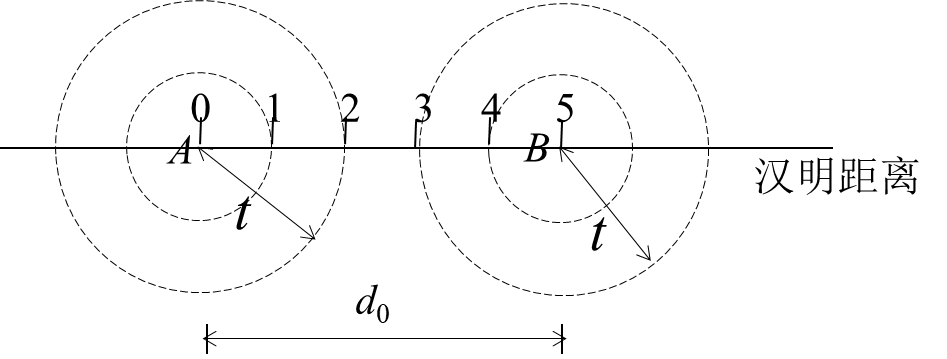
汉明距离

两个码字之间的汉明距离就是他们在相同位上不同码符号的数目的总数。

特性：非负性，对称性，三角不等式 D(X,Z)+D(Y,Z)≥D(X,Y)

码组C的最小距离

在二元码组C中，任意两个码字的汉明距离的最小值，称为码C的最小距离。

Dmin越大，抗干扰能力越强

自动要求重发(ARQ)系统（三种）：采用检错重发的系统

1.停止等待ARQ系统 

每发送一组码组，只有等收到ACK确认答复后才会继续发送下一组，处于半双工状态，效率较低。

2.拉后ARQ系统

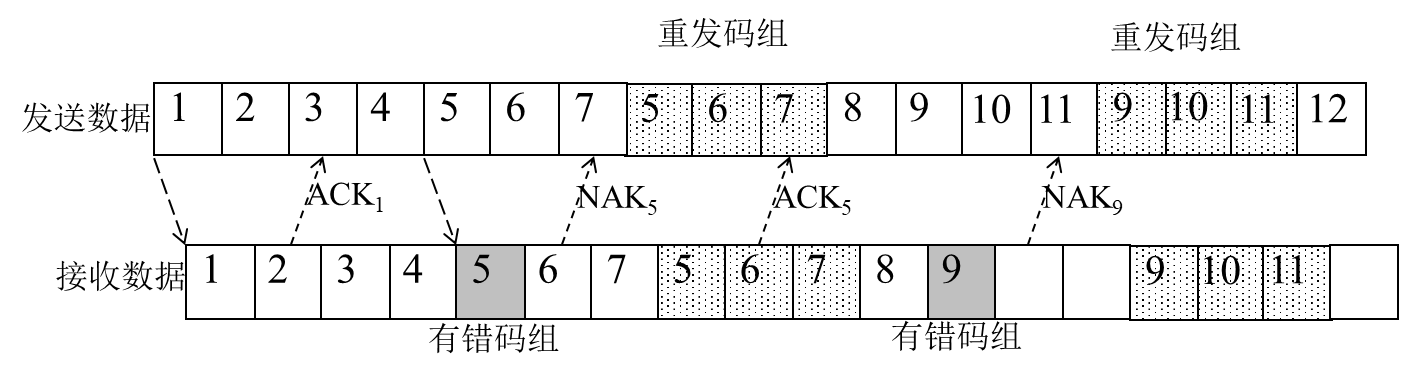
连续发生，当收到NAK答复时，从收到错误码组开始重发，需要对数据组和答复进行编号，双工信道，设备较复杂

3.选择重发ARQ系统

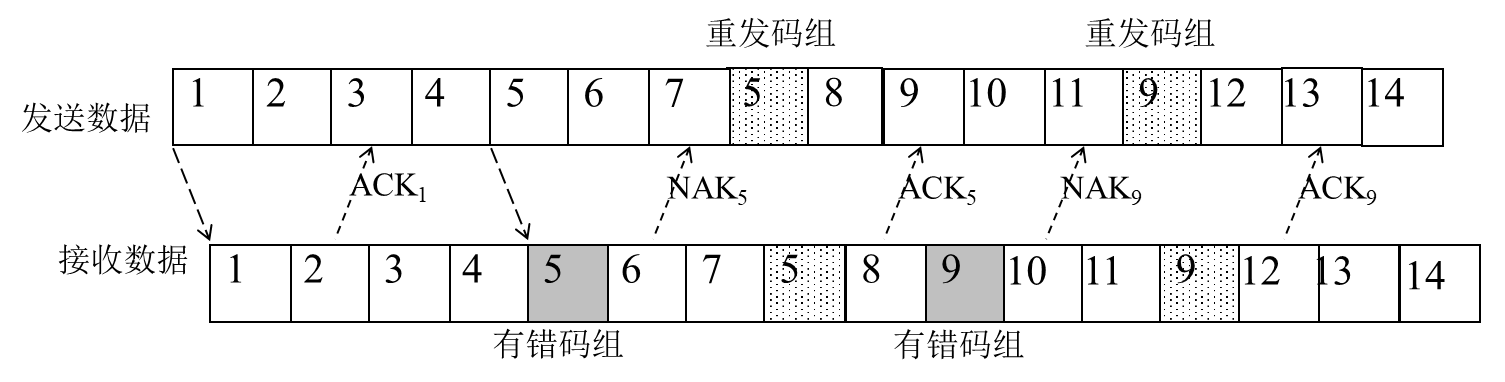
只重发出错的单个码组，提高效率

优点

与前向纠错方法相比，ARQ的优点：

1.监督码原较少就可使误码率降到很低

2.检错的计算复杂度较低

3.检错用的编码方法和加性干扰的统计特性基本无关，能适应不同特性的信道

缺点

与前向纠错方法相比，ARQ的缺点：

1.需要双向信道来重发，不能用于一点到多点的通信系统

2.重发将会使ARQ系统的传输效率降低

3.信道干扰严重时，不停的重发将会造成通信中断

4.实时通信例如电话通信就不能使用ARQ法

线性分组码

从信道输入端个n长二元序列中找出一组个码字，使码字的r=n-k个校验位与其k个信息位之间满足一定的线性关系。

模2线性方程，若k=3，n=7

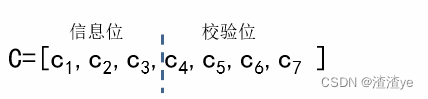
校验位由一下方程获得

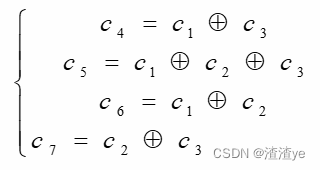
校验方程（监督方程）：是一种从信息位得到校验位的规则

校验矩阵

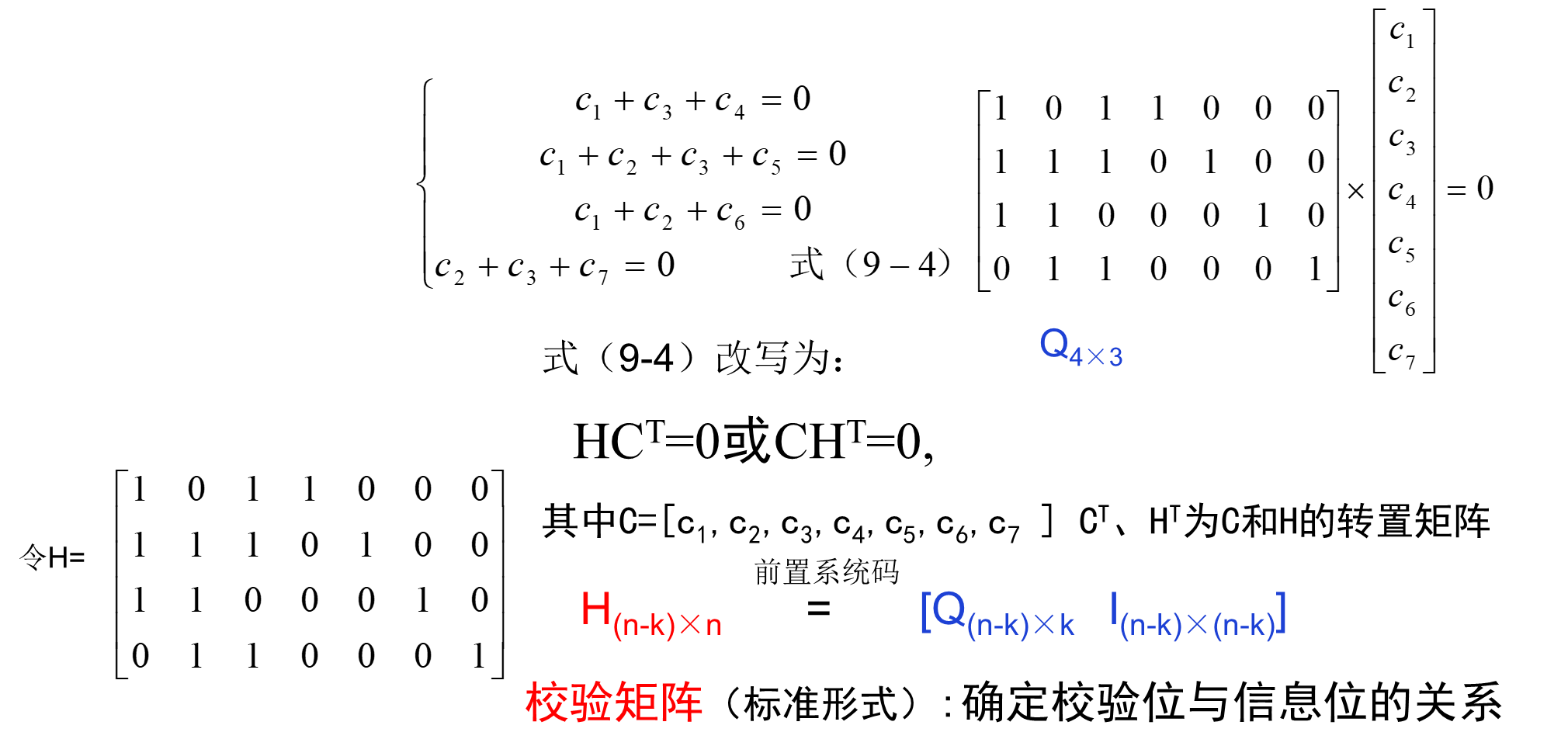
H阵的（n-k）行代表校验方程，这n-k个校验方程必须是线性无关的，H阵的秩R(H)=r=n-k

生成矩阵

码字C为信息组m和生成矩阵G各行的线性组合（和为“模2和”）

G中任意一行都是一个合法码字

任意两个码字之和仍然是一个合法码字

任意k个线性无关的码字可构成生成矩阵G

生成矩阵G与校验矩阵H的关系

  或者  

线性分组码的生成矩阵G与校验矩阵H的行向量彼此正交

P与Q互为转置矩阵

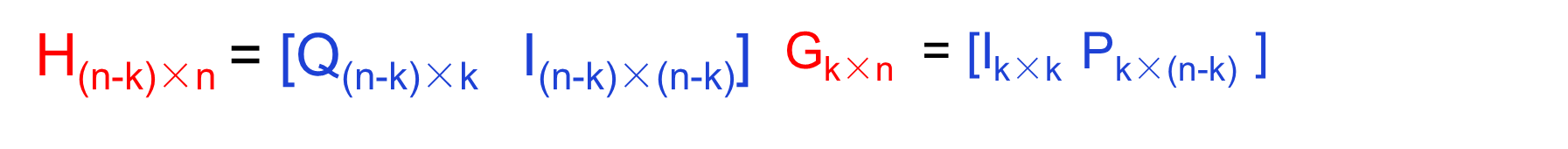
对偶码

（7，3）线性码的对偶码为（7，4）线性码

（7，3）线性码的校验矩阵H(7,3)是（7，4）码的生成矩阵G(7,4)

纠检错能力：与码的最小汉明距离有关

对于一个二进制对称信道，若输入为k个等可能的n长码字，则最大后验概率译码规则应为最小汉明距离译码。

（n，k）线性分组码

        e为检测的错码

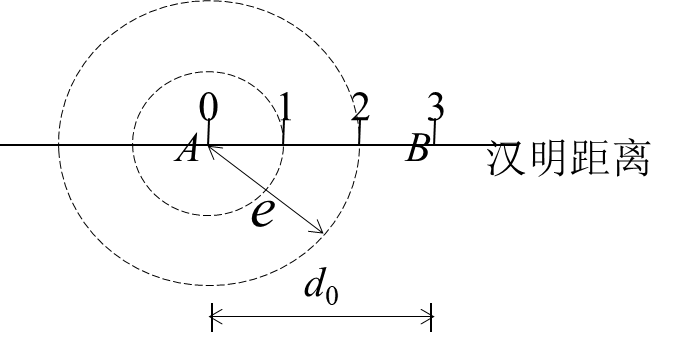
        t为纠正的错码

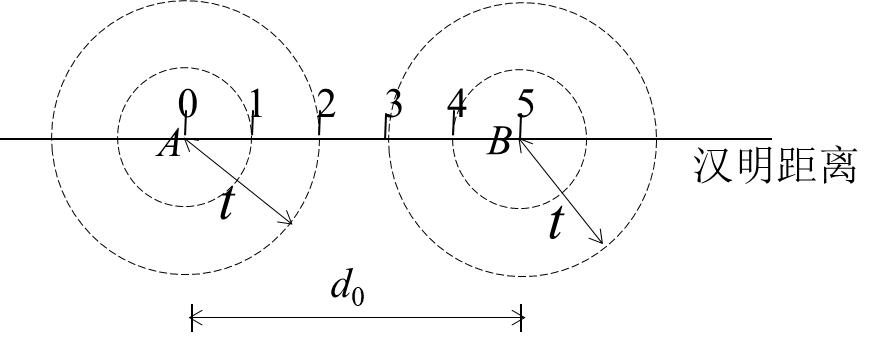
        纠正t个错码的同时检测e个错码（e>t）

注意：检错和纠错公式不能同时成立或同时运用

当错码数量少时，系统按前向纠错方式工作，以节省重发时间，提高传输效率；

当错码数量多时，系统按反馈重发方式纠错，以降低系统的总误码率。

汉明重量

码字中非零元素的个数之和称为汉明重量Wc

eg：C=[101010]，Wc=3

注意：线性分组码的最小距离等于非零码字的最小重量

对于（n，k）线性分组码，校验矩阵为H，若H中人与t列线性无关，而有t+1列线性相关，则码字的最小距离为dmin=t+1；若dmin=t+1，则校验矩阵H的任意t列线性无关，而有t+1列线性相关。

线性分组码的伴随式

发送码字为C，接受码字为Y，校验矩阵为H，可用利用H来校验Y是否正确

 或者 

0向量：无错误，即Y是一个码字

非0向量：有错误，即在传输中出现错误

意义：S是否为零是检验码字在传输过程中是否有错的标志

 或者  称为接受码字Y的伴随式（或监督子，校验子等）

错误图样E

E=[e1,e2,....,en ]

第i位出错，ei=1，无错为0

接收到的码字Y应该是发送码字C与错误图样E的和，即

         Y=C+E=[y1,y2,....,yn ]

其中，yi=ei+ci,+为模2加（异或）

由上述式子可得出结论：

伴随式S仅与错误图样E有关，与发送码字C无关

定理：

若(n,k)线性分组码能纠正t个错误，则其校验位的数目(n-k)必须满足：

等号成立时，称为完备码，其由码的纠错能力所确定的伴随式与错误图样个数相等，完备码的n-k个校验位都得到了充分利用

文章来源: blog.csdn.net，作者：渣渣ye，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/yyfloveqcw/article/details/124652493