信息论与编码技术之离散信道及其容量总结
目录
二.离散无记忆信道DMC(基本概念,几种常用的DMC的定义,I(X;Y)计算)
3.二元对称信道的平均互信息量:(重点:推导,公式,图,参数,含义)
五.离散无记忆N次扩展信道(重点:概念,信道矩阵求法,定理证明)
2.常见离散信道的信道容量(重点:信道特点,信道容量的计算,最佳分布)
4.独立并联信道(注意:根据输入分布判断是否为独立并联信道)
5.串联信道(重点:平均互信息量和信道容量的计算;数据处理定理的叙述和意义)
前言:
四个基本概念:
一个图:维拉图
一个基本原则:获取信息的过程就是减小不确定性的过程
一.分类与信道数学模型(概念)
数学模型:{X,p(y|x),Y},p(y|x)称为传递概率或转移概率
分类
二.离散无记忆信道DMC(基本概念,几种常用的DMC的定义,I(X;Y)计算)
1.离散无记忆信道DMC的充要条件(掌握证明,含义)

含义:离散信道在i时刻的输出yi(i=1,2,…N)只与i时刻的输入xi(i=1,2,…N)有关,与i时刻之前的输入和输出都无关,所以该信道是离散无记忆信道。
且i时刻的输出yi(i=1,2,…N)与i时刻的以后的输入xi(i=1,2,…N)无关,这表明离散无记忆信道的“无预感性”。
2.平稳信道
对任意正整数m、n,ai∈A,bj ∈B,若离散无记忆信道的转移概率还满足

含义:平稳信道的转移概率p(y︱x)不随时间变化。
二元对称信道(BSC)

二元删除信道(BEC)

二元对称消失信道

三.信道疑义度(重点:概念,含义,计算)
1.损失熵

含义:表示输出端在收到全部符号Y后,对输入X上存在的平均不确定程度。
它表示信源符号经过有噪信号传输后损失的信息量。

等于X本身具有的不确定性,减去收到Y后帮助X消除的不确定性。
H(X|Y) ≤H(X),当X与Y相互独立时取等号。
注意:
 不一定成立
不一定成立
2.矩阵计算

四.平均互信息量(重点:概念,两个定理,计算)
1.定义
2.两个定理(定义式,含义)
对于固定信道(即p(yj|xi)固定,对i,j), I(X;Y)是信源概率分布p(xi)的上凸函数。
对于固定信源分布p(xi),平均互信息量I(X;Y)是p(yj|xi)的下凸函数。
3.二元对称信道的平均互信息量:(重点:推导,公式,图,参数,含义)

固定信道:

五.离散无记忆N次扩展信道(重点:概念,信道矩阵求法,定理证明)
1.概念

数学模型: ![]()
N次扩展信道的信道矩阵:

即N次扩展信道矩阵中各行之和为1
2.信道矩阵求法
3.定理(重点:证明,含义)
若信道的输入和输出分别是 N长序列X和Y,且信道是无记忆的,亦即信道的传递概率为:

则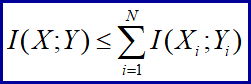
取等号的充要条件:信源无记忆
含义:信道无记忆时,N长序列X和Y的平均互信息量I(X;Y)小于或等于单个随机变量Xi和Yi的互信息量I(Xi;Yi)之和。
若信道输入和输出分别是 N长序列X和Y,且信源是无记忆的:

则 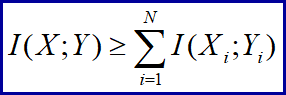
取等号的充要条件:信道无记忆
含义:信道无记忆时,N长序列X和Y的平均互信息量I(X;Y)小于或等于单个随机变量Xi和Yi的互信息量I(Xi;Yi)。
从上述证明可知,当信道和信源均无记忆时:

对于离散无记忆N次扩展信道:

六.信道容量(概念定义,常见离散信道的信道容量求法)
1.信道的大小定义
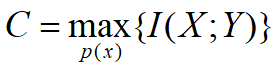
单位:bit/符号,达到C的p(x)为最佳输入分布
说明:C是信道传输信息量的最大能力。是某个固定信道的最大信息传输率。只与信道统计特性有关,与信源分布无关。
2.常见离散信道的信道容量(重点:信道特点,信道容量的计算,最佳分布)
无损有噪信道:一个输入对应多个互不相交的输出

无噪有损信道:一个输入唯一对应一个输出;一个输出可对应多个互不相交的输入。

无损确定信道(无损无噪信道):输入输出一一对应,信道矩阵P是单位阵

离散对称信道:

离散均匀信道:

离散准对称信道:

3.离散无记忆N次扩展信道

条件:信源无记忆,且每个单符号信道的输入Xi都达到最佳分布
4.独立并联信道(注意:根据输入分布判断是否为独立并联信道)

条件:信源无记忆,且每个单符号信道的输入Xi都达到最佳分布
5.串联信道(重点:平均互信息量和信道容量的计算;数据处理定理的叙述和意义)


七.信道剩余度(重点:概念,计算,理解含义)

从无损信道的相对剩余度角度来解释香农第一定理(香农无失真信源编码定理)(重点掌握)
信源编码就是将信源S输出的消息变换成新信源X的消息来传输,而使新信源的符号接近等概分布,新信源的熵接近最大熵logr。新信源的消息通过信道的信息传率 接近最大值(logr),信道的剩余度接近于0,使信源和信道达到匹配,信道得到充分利用。这就是香农无失真信源编码定理的基本思想。
文章来源: blog.csdn.net,作者:渣渣ye,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/yyfloveqcw/article/details/124392148
- 点赞
- 收藏
- 关注作者




评论(0)