Visual Studio 2019下用 C# 实现 Hill2 二阶希尔密码 的加密、解密 GUI界面

举报
小哈里 发表于 2022/05/11 01:07:50 2022/05/11
【摘要】 1、什么是Hill2 什么是Hill密码 希尔密码（Hill）使用每个字母在字母表中的顺序作为其对应的数字，即 A=0，B=1，C=2 等，然后将明文转化为 n 维向量，跟一个 n × n 的矩阵相乘...

1、什么是Hill2

什么是Hill密码

  • 希尔密码（Hill）使用每个字母在字母表中的顺序作为其对应的数字，即 A=0，B=1，C=2 等，然后将明文转化为 n 维向量，跟一个 n × n 的矩阵相乘，再将得出的结果模 26。
  • 注意用作加密的矩阵（即密匙）在 必须是可逆的，否则就不可能解码。只有矩阵的行列式和26互质，才是可逆的。

Hill2指的是n=2时，即加密矩阵为2 × 2，明文转为2维向量时候的加密。是Hill最简单的情况。

举个例子：

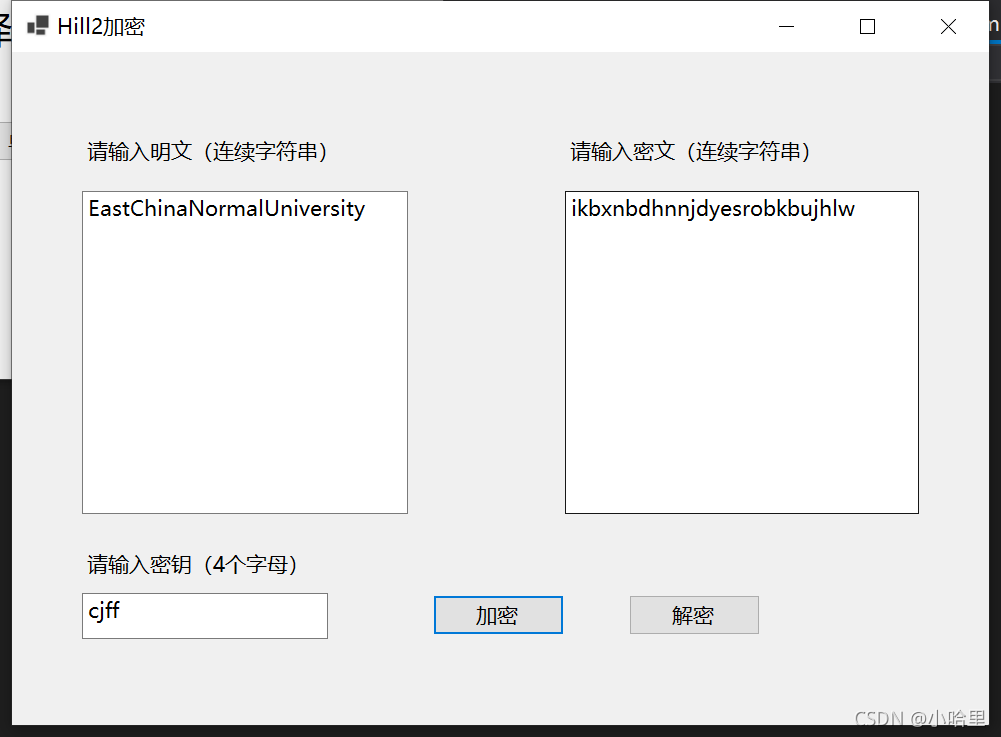
  • 明文串 x = EastChinaNormalUniversity，密钥 = [[2, 5],[9,5]] 或 “cjff”。

加密过程：

  • 加密：密文向量 = 明文向量 * 密钥矩阵 (mod 26)

  • 先将明文串对应英文字母编码表进行数字转化：
    4 0 18 19 2 7 8 13 0 13 14 17 12 0 11 20 13 8 21 4 17 18 8 19 24

  • 然后两两一组写成矩阵形式：
    在这里插入图片描述
    发现少了一个，所以在最后做补0处理（即补字符a）

  • 加密的过程就是矩阵乘法，前行乘后列，记得膜26（不膜会乱码！！）
    在这里插入图片描述

  • 得到密文矩阵后，按照分组对应的向量转成字母
    ikbxnbdhnnjdyesrobkbujhlw

解密过程：

  • 解密和加密差不多，就是先计算出原本密钥矩阵的逆矩阵，再直接乘密文就可以了。
  • 二阶矩阵的逆矩阵公式为：
    在这里插入图片描述
  • 求逆矩阵的时候记得用逆元，求出逆矩阵后记得膜26。（逆元记得用拓展欧几里得！不要用快速幂）
    比如 [[2, 5],[9,5]] 会得到 [ [ 11, 5 ], [ 1 , 20 ] ]。
  • 最后用上面一样的方法去乘以密文即可。

2、C#代码实现

在这里插入图片描述

using System;
using System.Windows.Forms;

namespace 古典加密系列
{
    public partial class Form5 : Form
    {
        public Form5()
        {
            InitializeComponent();
        }

        //数学函数，快速幂，逆元，公约数
        //public static int pows(int a, int x, int p) { if (x == 0) return 1; int t = pows(a, x >> 1, p); if (x % 2 == 0) return t * t % p; return t * t % p * a % p; }
        //public static int inv(int x, int p) { return pows(x, p - 2, p); }
        public static void EXGCD(int a, int b, ref int d, ref int x, ref int y, int MOD) { if (b==0) { d = a; x = 1; y = 0; } else { EXGCD(b, a % b,ref d,ref y,ref x, MOD); y -= x * (a / b); } }
        public static int inv(int a, int MOD) { int d=0, x=0, y=0; EXGCD(a, MOD, ref d, ref x, ref y, MOD); return d == 1 ? (x + MOD) % MOD : -1; }
        public static int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }


        //字符串函数，判断是否只由字母组成，字符串大写转小写
        public static bool check(string str)
        {
            bool ok = true;
            for (int i = 0; i < str.Length; i++)
            {
                if (str[i] >= 'a' && str[i] <= 'z') continue;
                if (str[i] >= 'A' && str[i] <= 'Z') continue;
                ok = false; break;
            }
            return ok;
        }
        public static string xiaoxie(string str)
        {
            string res = "";
            for (int i = 0; i < str.Length; i++)
            {
                if (str[i] >= 'a' && str[i] <= 'z') res = res + str[i];
                if (str[i] >= 'A' && str[i] <= 'Z') res = res + Convert.ToChar(str[i] + ('a' - 'A'));
            }
            return res;
        }

        //2阶Hill密码，加密和解密
        public static string jiami(string plaintext, string key)
        {
            key = xiaoxie(key);
            plaintext = xiaoxie(plaintext);

            int[,] A = new int[2, 2]{
                {key[0]-'a', key[2]-'a'},
                {key[1]-'a', key[3]-'a'}
            };

            int t = A[1, 1] * A[0, 0] - A[1, 0] * A[0, 1];
            t = (t % 26 + 26) % 26;
            if (gcd(t, 26) != 1)
            {
                MessageBox.Show("矩阵的行列式和26需要互质，否则没有逆矩阵");
                return "";
            }

            //两个字母组成向量进行加密，不够就补0
            int flag = 0;
            if (plaintext.Length % 2 == 1)
            {
                flag = 1;
                plaintext = plaintext + 'a';
            }
            //两两一组写成矩阵形式
            int[,] X = new int[2, plaintext.Length / 2];
            int cnt = 0;
            for (int i = 0; i < plaintext.Length; i++)
            {
                if (i % 2 == 0) X[0, cnt] = plaintext[i] - 'a';
                else
                {
                    X[1, cnt] = plaintext[i] - 'a';
                    cnt++;
                }
            }
            //矩阵乘法
            int[,] Y = new int[2, plaintext.Length / 2];
            for (int i = 0; i < 2; i++)
            {
                for (int j = 0; j < plaintext.Length / 2; j++)
                {
                    int tmp = 0;
                    for (int k = 0; k < 2; k++)
                    {
                        tmp += A[i, k] * X[k, j];
                    }
                    Y[i, j] = tmp%26;
                }
            }
            string res = "";
            for (int i = 0; i < plaintext.Length / 2; i++)
            {
                char ch = (char)(Y[0, i]+'a');
                res = res + ch;
                ch = (char)(Y[1, i]+'a');
                res = res + ch;
            }
            if(flag == 1)
            {
                res = res.Substring(0, res.Length - 1);
            }
            return res;
        }

        public static string jiemi(string plaintext, string key)
        {
            key = xiaoxie(key);
            plaintext = xiaoxie(plaintext);

            //逆矩阵
            int a = key[0] - 'a', b = key[2] - 'a', c = key[1] - 'a', d = key[3] - 'a';

            int t = ((a * d - b * c) % 26+26)%26;
            if (gcd(t, 26) != 1)
            {
                MessageBox.Show("矩阵的行列式和26需要互质，否则没有逆矩阵");
                return "";
            }
            t = inv(t,26)%26;
            int aa = d * t % 26, bb = (-b * t % 26 + 26) % 26, cc = (-c * t % 26 + 26) % 26, dd = a * t % 26;

            int[,] A = new int[2, 2]{
                {aa,bb },
                {cc,dd }
            };


            //两个字母组成向量进行解密，不够就补0
            int flag = 0;
            if (plaintext.Length % 2 == 1)
            {
                flag = 1;
                plaintext = plaintext + 'a';
            }
            //两两一组写成矩阵形式
            int[,] X = new int[2, plaintext.Length / 2];
            int cnt = 0;
            for (int i = 0; i < plaintext.Length; i++)
            {
                if (i % 2 == 0) X[0, cnt] = plaintext[i] - 'a';
                else
                {
                    X[1, cnt] = plaintext[i] - 'a';
                    cnt++;
                }
            }
            //矩阵乘法
            int[,] Y = new int[2, plaintext.Length / 2];
            for (int i = 0; i < 2; i++)
            {
                for (int j = 0; j < plaintext.Length / 2; j++)
                {
                    int tmp = 0;
                    for (int k = 0; k < 2; k++)
                    {
                        tmp += A[i, k] * X[k, j];
                    }
                    Y[i, j] = tmp % 26;
                }
            }
            string res = "";
            for (int i = 0; i < plaintext.Length / 2; i++)
            {
                char ch = (char)(Y[0, i] + 'a');
                res = res + ch;
                ch = (char)(Y[1, i] + 'a');
                res = res + ch;
            }
            if (flag == 1)
            {
                res = res.Substring(0, res.Length - 1);
            }
            return res;
        }

		//GUI按钮
        private void button1_Click(object sender, EventArgs e)
        {
            string key = textBox3.Text;
            if (key.Length != 4 || check(key) == false)
            {
                MessageBox.Show("密钥输入错误，请重新输入密钥");
                return;
            }

            string plaintext = textBox1.Text;
            if (check(plaintext) == false)
            {
                MessageBox.Show("明文输入错误，请重新输入明文");
                return;
            }

            string ciphertext = jiami(plaintext, key);
            textBox2.Text = ciphertext;
        }

        private void button2_Click(object sender, EventArgs e)
        {
            string key = textBox3.Text;
            if (key.Length != 4 || check(key) == false)
            {
                MessageBox.Show("密钥输入错误，请重新输入密钥");
                return;
            }

            string plaintext = textBox2.Text;
            if (check(plaintext) == false)
            {
                MessageBox.Show("明文输入错误，请重新输入明文");
                return;
            }

            string ciphertext = jiemi(plaintext, key);
            textBox1.Text = ciphertext;
        }
    }
}



  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    • 
  
  • 40
    • 
  
  • 41
    • 
  
  • 42
    • 
  
  • 43
    • 
  
  • 44
    • 
  
  • 45
    • 
  
  • 46
    • 
  
  • 47
    • 
  
  • 48
    • 
  
  • 49
    • 
  
  • 50
    • 
  
  • 51
    • 
  
  • 52
    • 
  
  • 53
    • 
  
  • 54
    • 
  
  • 55
    • 
  
  • 56
    • 
  
  • 57
    • 
  
  • 58
    • 
  
  • 59
    • 
  
  • 60
    • 
  
  • 61
    • 
  
  • 62
    • 
  
  • 63
    • 
  
  • 64
    • 
  
  • 65
    • 
  
  • 66
    • 
  
  • 67
    • 
  
  • 68
    • 
  
  • 69
    • 
  
  • 70
    • 
  
  • 71
    • 
  
  • 72
    • 
  
  • 73
    • 
  
  • 74
    • 
  
  • 75
    • 
  
  • 76
    • 
  
  • 77
    • 
  
  • 78
    • 
  
  • 79
    • 
  
  • 80
    • 
  
  • 81
    • 
  
  • 82
    • 
  
  • 83
    • 
  
  • 84
    • 
  
  • 85
    • 
  
  • 86
    • 
  
  • 87
    • 
  
  • 88
    • 
  
  • 89
    • 
  
  • 90
    • 
  
  • 91
    • 
  
  • 92
    • 
  
  • 93
    • 
  
  • 94
    • 
  
  • 95
    • 
  
  • 96
    • 
  
  • 97
    • 
  
  • 98
    • 
  
  • 99
    • 
  
  • 100
    • 
  
  • 101
    • 
  
  • 102
    • 
  
  • 103
    • 
  
  • 104
    • 
  
  • 105
    • 
  
  • 106
    • 
  
  • 107
    • 
  
  • 108
    • 
  
  • 109
    • 
  
  • 110
    • 
  
  • 111
    • 
  
  • 112
    • 
  
  • 113
    • 
  
  • 114
    • 
  
  • 115
    • 
  
  • 116
    • 
  
  • 117
    • 
  
  • 118
    • 
  
  • 119
    • 
  
  • 120
    • 
  
  • 121
    • 
  
  • 122
    • 
  
  • 123
    • 
  
  • 124
    • 
  
  • 125
    • 
  
  • 126
    • 
  
  • 127
    • 
  
  • 128
    • 
  
  • 129
    • 
  
  • 130
    • 
  
  • 131
    • 
  
  • 132
    • 
  
  • 133
    • 
  
  • 134
    • 
  
  • 135
    • 
  
  • 136
    • 
  
  • 137
    • 
  
  • 138
    • 
  
  • 139
    • 
  
  • 140
    • 
  
  • 141
    • 
  
  • 142
    • 
  
  • 143
    • 
  
  • 144
    • 
  
  • 145
    • 
  
  • 146
    • 
  
  • 147
    • 
  
  • 148
    • 
  
  • 149
    • 
  
  • 150
    • 
  
  • 151
    • 
  
  • 152
    • 
  
  • 153
    • 
  
  • 154
    • 
  
  • 155
    • 
  
  • 156
    • 
  
  • 157
    • 
  
  • 158
    • 
  
  • 159
    • 
  
  • 160
    • 
  
  • 161
    • 
  
  • 162
    • 
  
  • 163
    • 
  
  • 164
    • 
  
  • 165
    • 
  
  • 166
    • 
  
  • 167
    • 
  
  • 168
    • 
  
  • 169
    • 
  
  • 170
    • 
  
  • 171
    • 
  
  • 172
    • 
  
  • 173
    • 
  
  • 174
    • 
  
  • 175
    • 
  
  • 176
    • 
  
  • 177
    • 
  
  • 178
    • 
  
  • 179
    • 
  
  • 180
    • 
  
  • 181
    • 
  
  • 182
    • 
  
  • 183
    • 
  
  • 184
    • 
  
  • 185
    • 
  
  • 186
    • 
  
  • 187
    • 
  
  • 188
    • 
  
  • 189
    • 
  
  • 190
    • 
  
  • 191
    • 
  
  • 192
    • 
  
  • 193
    • 
  
  • 194
    • 
  
  • 195
    • 
  
  • 196
    • 
  
  • 197
    • 
  
  • 198
    • 
  
  • 199
    • 
  
  • 200
    • 
  
  • 201
    • 
  
  • 202
    • 
  
  • 203
    • 
  
  • 204
    • 
  
  • 205
    • 
  
  • 206
    • 
  
  • 207
    • 
  
  • 208
    • 
  
  • 209
    • 
  
  • 210
    • 
  
  • 211
    • 
  
  • 212
    • 
  
  • 213
    • 
  
  • 214
    • 
  
  • 215
    • 
  
  • 216
    • 
  
  • 217
    • 
  
  • 218
    • 
  
  • 219
    • 
  
  • 220
    • 
  
  • 221
    • 
  
  • 222
    • 
  
  • 223
    • 
  
  • 224
    • 
  
  • 225
    •

3、参考资料

https://ctf-wiki.org/crypto/classical/polyalphabetic/#hill
https://zhuanlan.zhihu.com/p/328562250
https://wenku.baidu.com/view/f1b150cd51e79b8969022619?pn=2&pu=sl@1,pw@500,sz@224_220,pd@1,fz@2,lp@3,tpl@color,
http://www.go60.top/wenzhang/juzhen/14.html
https://matrix.reshish.com/zh/inverse.php
https://wenku.baidu.com/view/b0525966f5335a8102d22078.html

文章来源: gwj1314.blog.csdn.net，作者：小哈里，版权归原作者所有，如需转载，请联系作者。

原文链接：gwj1314.blog.csdn.net/article/details/120953338

【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
C# UI Visual Studio
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入